搞懂“圆”来如此，解决最值问题

搞懂“圆”来如此，解决最值问题

李耀培

佛山市三水区西南街道金本中学

【摘要】数学问题很多都是动态问题，但动态当中又存在着静态关系，而轨迹圆就是常见的一种静态关系。本文通过若干例子说明轨迹圆的确定，再借助基本图形“一箭穿心”解决轨迹圆中的几何最值问题，阐述对通法通解的理解与关注.

【关键词】轨迹圆静态关系 一箭穿心 最值

【正文】

1.基本图形“一箭穿心”的证明

命题：外一点P与圆心O相连，交于A,B两点（其中B点比A点更接近点P），则点到圆O上各点所连线段中，最长，最短.

已知：如图1，点是外一点，连接并延长，依次交于、两点.

求证：与上各点连线中，最长，最短.

证明：在上任意取一点（不同于点），连接并延长，交于点.

连接，，

由三角形三边关系：

在△中：，

∵，，

∴，

∴，

基于点的任意性，因此最短恒成立.                                

在△中：，

∵，，                               

∴，                                        图1

基于点的任意性，因此最长恒成立.

2. 轨迹圆类型一：定义圆

圆的定义：在一个平面内，到一定点的距离等于定长的所有点的集合叫做圆。

问题1：有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，，点，分别在射线，上，长度始终保持不变，，为的中点，点到，的距离分别为4和2．在此滑动过程中，猫与老鼠的距离的最小值为____________．

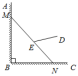
分析：因为线段MN虽然在动，但长度不变，点E在动，但点E始终是线段的中点，，点B是定点，这都是动态问题中的静态关系，连接BE，由“直角三角形斜边上的中线等于斜边的一半”，易得重要的静态关系：，则根据圆的定义，点E必在以点B为圆心，2为半径的圆弧上，找出动点E是“轨迹圆”是解决这个题目的关键，再利用基本图形“一箭穿心”解决最值问题.

问题2：（2021•荔湾区三模）如图，在矩形纸片中，，，点是的中点，点是边上的一个动点，将沿所在直线翻折，得到△，则线段的最小值是 ________________．

分析：因为点F在动，所以线段EF在动，折叠后的对应点在动，但利用折叠前后对应线段相等这一静态关系可以得到，即动点是以点为圆心，2为半径的轨迹圆，找出动点是“轨迹圆”是解决这个题目的关键，再利用基本图形“一箭穿心”解决最值问题.

总结：对于“到一定点的距离等于定长的动点轨迹集合”此类问题，可以由圆定义得到“轨迹圆”，再利用基本图形“一箭穿心”解决最值问题.

总结：遇到动点题的时候，看看能不能直接或间接推出“定弦定角模型”，从而得到“轨迹圆”，是解题时候常用的一种思路，如果有，则再利用基本图形“一箭穿心”解决最值问题.

数学要通过解题总结后发现一类问题中的共性，才能做到触类旁通，举一反三，本文从定义出发：到定点的距离都等于定长的所有点确定一个圆，再从“直角圆周角模型”这一特殊性到“定弦定角”这种一般规律，说明在动点问题中发现“轨迹圆”的重要性，从而使解题方法更具有一般性，凸显通解通法.

【参考文献】

[1] 陈光祥.“基本模型”专题复习的示例和思考.中学数学参考（中旬），2018年第11期：31-33

[2]叶春泉.析疑难之诸因，探求解之通法.中学数学（初中）2018年12月：80-82

[3]莫焯洪.凸显作圆共性，利用“基本图形”解决最值问题.