假设检验在订货问题中的应用

假设检验在订货问题中的应用

夏燕

武警警官学院  （四川成都  610213）

摘要：订货问题中常常需要对产品的次品率进行抽样检测，供应商声称一批产品的次品率不会超过某个标称值，那么企业如何设计抽样检测方案，使得检测次数尽可能的少，同时又能保证置信度，假设检验可以解决上述问题。

关键词：订货问题；次品率；抽样检测；假设检验

引言

某企业生产某种畅销的电子产品，需要分别购买两种零配件（零配件 1 和零配件 2），在企业将两个零配件装配成成品。在装配的成品中，只要其中一个零配件不合格，则成品一定不合格；如果两个零配件均合格，装配出的成品也不一定合格。对于不合格成品，企业可以选择报废，或者对其进行拆解，拆解过程不会对零配件造成损坏，但需要花费拆解费用。

供应商声称一批零配件（零配件 1 或零配件 2）的次品率不会超过某个标称值。企业准备采用抽样检测方法决定是否接收从供应商购买的这批零配件，检测费用由企业自行承担。请为企业设计检测次数尽可能少的抽样检测方案。如果标称值为10%，根据你们的抽样检测方案，针对以下两种情形，分别给出具体结果：

(1) 在95%的信度下认定零配件次品率超过标称值，则拒收这批零配件；

(2) 在90%的信度下认定零配件次品率不超过标称值，则接收这批零配件。

一、假设检验的基本原理

假设检验基于实际推断原理，即小概率事件在一次试验中几乎不可能发生。其与最大似然原理是一致的，即在一次试验中概率最大的事件最有可能发生，或者在一次试验中发生的事件我们认为其概率最大。二者都是英国著名统计学家费歇尔提出的。

二、假设检验的基本步骤

第一步，提出原假设和备择假设；

第二步，确定检验统计量和显著性水平；

第三步，给出拒绝域；

第四步，带入数据，计算检验统计量，若落入拒绝域，则拒绝

原假设，选择备择假设，否则接受原假设。

针对问题（1）假设检验具体步骤如下：

分析这个问题：我们要借助于反证法及小概率原理。我们不妨提出这样的假设：（次品率不超过标称值）；

（次品率超过标称值）。

在成立的前提下，依据中心极限定理，当时，检验统计量近似服从正态分布，拒绝域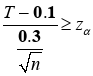，通过matlab可以分别计算时的样本容量。从而得到样本容量和对应的次品数不等式，不等式成立则拒绝原假设，拒收该批产品，否则，接受原假设。

问题（1）对应的拒绝域为 ，例如，在95%的信度下，我们假设抽到的次品数为0，抽样检测40件，若次品数超过7件，则拒收这批产品。

问题（2）的接受域域为，例如，在90%的信度下抽样检测40件，若次品数不超过6件，则接受这批产品。

三、模型分析

假设检验可能范两类错误 ——犯第Ⅰ类错误，或者“弃真”错误； ——犯第Ⅱ类错误，或者“取伪”错误．

既然可能犯两类错误，我们当然希望能将犯错的概率都控制一下，那么这两类能否同时控制呢？实际上，样本容量固定的情况下，不能同时控制犯两类错误的概率，他们的关系好比翘翘板，我们必须舍弃其中一个．为了节约企业的检测成本，使检测次数尽可能的少，依据中心极限定理，可以取最小值40，并且可以计算得出次品数的阈值，同时也能保证一定的信度，这就是假设检验在产品订货问题中的应用。

四、模型优化

为了设计一个抽样检测方案以评估零配件的次品率，我们可以使用统计抽样的方法。通过上述的模型，可以根据具体的n和次品数值确定抽样检测方案。在实际应用中可根据需求进一步进行参数的调整与优化。例如，从n中先抽取三分之一，若次品率远远大于标称值，则直接拒收，若次品率远远小于标称值，则可以接收。要设计一个抽样检测方案，我们可以使用统计抽样原理，特别是二项分布的概念。根据二项分布的性质，我们可以通过设定样本容量大小和样本中不合格件数的阈值来实现我们的目标。这些方案可以帮助企业在不同信度下对零配件的质量进行有效控制，从而减少生产的不合格率和经济损失。编写代码可输出满足条件的样本大小和不合格零配件数量的阈值。当满足不同的条件时，企业可以根据检测结果决定是否接收或拒收这批零配件。

参考文献：

[1]赵寇鑫.考虑消费者渠道偏好的全渠道零售商订货决策[D].北京交通大学,2023.DOI:10.26944/d.cnki.gbfju.2023.000322.

[2]杨文.交叉销售产品定价与订货联合决策[D].南京理工大学,2023.DOI:10.27241/d.cnki.gnjgu.2023.000449.

[3]梁娜.威布尔分布下抽检方法设计与供应保障成本优化[D].电子科技大学,2022.DOI:10.27005/d.cnki.gdzku.2022.000228.

[4]刘桔.随机产出、需求和价格下基于分布鲁棒优化的订货决策和契约设计研究[D].华南理工大学,2022.DOI:10.27151/d.cnki.ghnlu.2022.005217.

[5]张学健,陈春艳,赵娜.计数抽样检验程序在检验检测机构质量管理中的应用[J].中国标准化,2024,(10):163-166.

[6]马立新,李彪,李少武,等.基于统计抽样原理的典型室温分布比例确定方法研究[J].暖通空调,2023,53(12):131-134+34.DOI:10.19991/j.hvac1971.2023.12.19.