赏析解思变——说题的实践与收获

赏析解思变——说题的实践与收获

朱慧明

浙江省台州市书生中学   318000

摘要  说题是提高教师专业水平发展的一条有效途径，以“说题活动”为载体，从赏题、析题、解题、思题、变题这几方面，促进教师的课堂教学改革，提升教师解题和命题的能力，同时也有利于培养学生的学习能力。通过“说题活动”，激发教师在教、学、研究等方面有新的突破。

关键词  数学说题  解题命题能力  专业发展

从“说课”到“说题”，教研活动的趋势正在发生着悄无声息的变化。笔者有幸曾参加过“说题”比赛，从听说“说题”到熟知“说题”，也深刻的意识到说题对于教师的成长与收获。接下来本文主要阐述说题比赛的实践过程和谈一点自己的想法与感悟。

一、说题的内涵与规范过程

数学说题是指教师对于一道题深入研究后，面对同行和专家，用语言来阐述对试题的理解。具体可以包括，以课程标准和考纲为指导，根据理论研究和学情分析，把握以生为本的原则，深层次地剖析试题背后的教学问题。说题是一种把握数学本质的新兴教研模式，极大的提升教师的专业能力水平。

说题比赛或活动主要有以下几个环节：

一是说试题的背景与来源；二说试题包含的相关的数学知识，比如已知条件和结论、概念、公式、定理等；三是说蕴含的数学思想方法，以实际知识体现数学思想，尽量避免离开知识空谈思想；四是解题方法，如何分析题目、如何书写解题步骤、用一题多解的方法考虑；五是变式拓展与延伸，可以改变已知条件或结论，可以对基本图形进行改编；六是回顾与反思，与教学相结合进行反思、反思解题方法、对试题的变式拓展的设计意图等。

二、说题案例分析

下面是以笔者参加的说题比赛试题为例加以分析说明：

题目  如图，在正方形ABCD中，点E在BC边上，连接AE，的平分线

AG与CD边交于点G，与BC的延长线交于点F．
点E是BC的中点,若AB=2，求线段CF的长．
连接EG，若EG⊥AF，求证：点G为CD边的中点．
说题要有以下三个方面：

1．试题的背景与立意

2．解题方法

3．变式与拓展

…………. （其余的请老师们自已添加，鼓励老师们有自己的东西）

（一）赏题

1.熟悉——试题的来源与背景

这是一题来自课本的习题改编题，来源于浙教版八年级下册第5章特殊平行四边形第127页课内练习第2题，同时我们也能在2020年杭州中考卷第21题看到此题，相似度更高。

（2020.杭州中考.21）如图，在正方形ABCD中，点E在BC边上，连接AE，∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．设＝λ（λ＞0）．

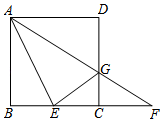（1）若AB＝2，λ＝1，求线段CF的长．

（2）连接EG，若EG⊥AF，                      

①求证：点G为CD边的中点．

②求λ的值．

2.全面——基本数学知识

试题包含初中基本数学知识点有正方形的性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质和角平分线的性质。

3.丰富——数学思想方法

从几何图形到求线段的长度、比值等题目体现了数形结合的思想；杭州卷从λ的值从特殊值1到任意，体现了从特殊到一般的数学思想；从结论中证明中点，我们把它转化为证明两条边相等，再进一步转化为证明两个三角形全等，体现了转化与化归的数学思想。

（二）析题

   千里之行始于足下，仔细的审题才是解题成功的第一步，也是重要的一步。波利亚在《怎样解题》中指出，弄清问题是解题的第一步。在审题过程中，可以划一划，圈一圈关键字。

分析： 已知条件：正方形ABCD，AG是∠DAE的角平分线。从题干的条件分析，AG是角平分线， 四边形ABCD是正方形也是特殊的平行四边形，具有所有特殊四边形的性质，所以会联想到角平分线遇平行线产生等腰三角形，能够知道AE=EF,第一小题已知点E是BC的中点，能够得到BE=EC，而已知条件知道AB的长，根据勾股定理我们就能求出AE的长，进一步可以得到CF=EF-CE。

第二小题已知EG⊥AF，题干能够推出△AEF是等腰三角形，我们就能联想到等腰三角形的三线合一，能够得出EG也是底边上的中线，即AG=GF。然后从结论出发，要证明点G是CD边的中点，只要证明DG=CG，而证明两条线段长度相等，我们一般采用证明两个三角形全等。

教学启示： 在平常的教学中，对于几何教学，我们要学会多追问学生，要引导学生从已知条件出发，或者从结论倒推，对于一些经典的条件要能够知道它们的用法，比如角平分线遇上平行线一定会产生等腰三角形。也要能够联想，注意在图上写写画画标注一下，培养几何解题的好习惯，更能够在教学上不断培养学生分析问题的能力，培养学生的逻辑推理思维和发散性思维。

（三）解题

（1）解 ∵E是BC的中点，且AB＝2，∴BE＝EC＝1，

         由勾股定理可得，AE＝.

         ∵AG平分∠DAE， ∴∠1＝∠2.

         ∵四边形 ABCD是正方形，∴AD//BC．

         ∴∠1＝∠

F．∴∠2＝∠F．

         ∴AE＝EF＝.∴CF＝EF-CE＝-1．

（2）解  由（1）可知，AE＝EF，∵EG⊥AF，

∴AG＝GF， ∵∠1＝∠F．∵∠3＝∠4．

∴△ADG≌△FCG(ASA).

         ∴DG＝CG，即点G为CD边的中点．

（四）变题

变式教学在数学教学中运用的最为广泛，通过教师例题的讲解，然后学生针对于同类型的题目进行变式练习，真正要让教师完全拥有原创自主命题的能力是比较困难的，但是要学会在题目的基础上进行改编，下面我从以下几方面进行改编：

1.改变点E的位置，让点E成为动点

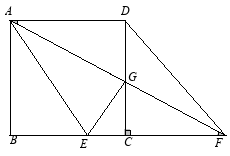
变式拓展1：如图，在正方形ABCD中，点E在直线BC上运动，且点E在点B、点C之间，连接AE，∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．若EG⊥AF，

①则与△ADG相似的三角形有哪几对？

②则的值为多少？

分析：点E在BC之间,且更特殊位置，EG⊥AF的时候，可以编制一些题型，比如相似三角形，比如长度的比值等等。

变式拓展2：如图，在正方形ABCD中，点E在直线BC上运动，且点E在点B、点C之间，连接AE,∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．在点E运动的过程中，M是AF上的动点，P是AE上的动点，若AB＝a，求ME+MP的最小值？(用a的代数式表示）

变式拓展3：如图，在正方形ABCD中，点E在直线BC上运动，且点E刚好与点C重合，连接AE，∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．若点E刚好运动到C，AB＝a，那么在线段AE上能否找到一点H，使得DH+GH的值最小？最小值为多少(用a的代数式表示）.若不存在，请说明理由.

变式拓展4：如图，在正方形ABCD中，点E在直线BC上运动，且点E在点B左边，连接AE，∠DAE的平分线AG与DC延长线交于点G，与BC边交于点F．在射线DC上取一点H，使得DH＝BE，则EF与GH有什么关系.

变式拓展5：如图，在正方形ABCD中，点E在直线BC的延长线上运动，且点E在点C右边，连接AE，∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．当时，则BC与CE有何数量关系？

设计意图：点E成为动点，在直线BC上运动，通过点E在点B左边、点E在BC边上、点E和点C重合、点E在点C右边这几种情况设计出不同类型的题目，但牢牢的抓住一条设计主线，E是直线BC上的动点。

2.改变图形的形状

变式拓展6：如图，在矩形ABCD中，点E在BC边上，连接AE，∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F．若AB=2，CE=1，问AD长为多少时，四边形AEFD为菱形．

变式拓展7：如图，在菱形ABCD中，∠B=30°，BE=AE=1，∠DAE的角平分线AF交CD于点G.求的值.

变式拓展8： 如图，在平行四边形ABCD中，∠DAB的平分线交BC延长线于点G,∠ABC的平分线交AD延长线于点H，证明:四边形ABGH是菱形.

变式拓展9：如图，梯形ABCD中，AD//BC，BD平分∠ABC，若BD⊥CD，AB=10,CD=12,求sin∠ABC.

设计意图：通过改变图形，从正方形改变成矩形、菱形、平行四边形、梯形，来命制一些不同的试题，设计的主线是抓住图形的改变。

三、说题的意义与收获

说题其实是把研究教、学和习题结合起来，拓宽了教学研究的领域。说题对教师们的要求很高，不仅要能够赏析题目，还要能够拓展题目，对教师的自身专业素质提出了更高的要求。

1.说题促进课堂教学改革

新课改强调要求变革学习方式，建立探究式教学，从而培养教师的研究能力，也能够引领学生，促进学生的自主发展，可以说数学说题为现在的课堂教学改革提供了良好的平台。

2.说题促进教学专业发展

说题要求教师做许多准备工作，比如查阅相关资料，认真研究试题来源、知识点等，这样自然而然促进教师对于教材的研究，掌握试题命制的技能、技巧。因此，说题活动有助于加强教师自身的学习，提高自身解题和命题能力，让教师不断的提高自身的专业素养，所以对于年轻教师有着非常大的帮助。

3.说题促进学校有效教研

学校教研注重对教材的处理，而不是试题的研究，缺乏教研的深度和广度。而说题能够将任务层层递进；通过一道试题，最基本的先说说考查的知识点，思想方法，命题意图等。其次，说说试题如何解，方法有几种，帮助教师提高解题能力，也促进课堂教学。最后，拓展试题，帮助教师提高命题试题能力，这样的说题活动给老师们提供相互学习、交流、研讨的平台，这样说题活动才是真正有效的教研。

总之，说题是一种好的教育研究形式，是教师发展的有效载体，能够不断促进教师的课堂教学，促进学生的学习，促进教师的解题命题能力，从而不断提高教师自身的专业水平发展。

参考文献：

[1]来林芳.赏·析·解·思·变——说题实践与收获[J].中国数学教育,2016(23):60-64.

[2]李云萍，方晓飞.说题说出别样天——摭谈初中数学教师说题[J].中国数学教育,2015(07):26-29.

[3]李永树.解题、说题、命题——初中数学教师教学成长“三部曲”[J].中学数学,2020(14):85-86.