水流一维非恒定流模型在河道洪水演算中的应用

水流一维非恒定流模型在河道洪水演算中的应用

葛婷

芜湖市河湖管理处 安徽芜湖 241000

[摘 要] 设计流量是河流治理最基础的数据，拟定河流各河段设计流量是规划专业的重要工作之一。水利工程中通常采用恒定流方法计算分析洪水运动情况，但对于径流大、洪峰大、水流复杂等河道，水利恒定流计算方法则误差较大。本文以青戈江为例，利用河道洪水演进数学模型，通过建立河流运动的一维非恒定流模型，对青戈江不同水情、不同工况条件进行了洪水演进分析，并通过与实际水文站资料进行对比，验证了计算的合理性。

[关键词] 洪水演算 非恒定流 数学模型

1、河流概况

青弋江为长江一级支流，发源于黄山，源头主河为清溪河，沿途流经陈村水库、泾县、宣城、南陵、芜湖等地，于芜湖汇入长江。青弋江流域总面积8178km²，河道全长297km。

青弋江从泾县县城以上为上游河段，长126 km，两岸山势陡峻，麻川、清溪等支流就穿行于高山狭谷之间。泾县以下至南陵西河镇45 km为中游河段，河宽80-130m，水面比降0.16-1.19‰。西河镇以下为下游，长104 km，沙质、淤泥质河床、河槽平直、水流平稳，两岸地势平坦、河网交织，为长江冲积平原组成部分。

青弋江水位及流量受降雨量变化影响较大，西河镇站多年平均水位10.36m，西河镇多年平均流量154m³/s。

2、洪水演算分析

青戈江是长江下游的重要支流，具有径流大、集流快、洪峰大等特点，同时青戈江属游荡型河床，水流复杂，采用恒定流无法计算准确洪水运动。为准确分析青戈江洪水运动情况，本次研究制定了青戈江河道洪水演进数学模型，通过建立青戈江河道水流运动的一维非恒定流模型，对青戈江不同水情、不同工况条件进行了洪水演算分析。

（1）数学模型的建立

一维非恒定流数学模型方程按下式计算:

连续方程：

（1）

运动方程：

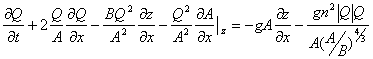（2）

式中：x为舜水流向坐标值；t为时间；Q为流量；Z为水位；A为横断面积；B为河道宽度；ql为变化的流量值；n为糙率；

对于边界情况，需考虑进段和出段，必要时需同时考虑一并带入计算方程，进段和出段边界均包括流量水位关系等数据

（2）计算过程

计算方式可选取某一段河道为计算单元并划分为小的网格，即使用有限元法进行河道分解，计算分析具体单元的水位流量关系。

计算中可按单元网格划分水流运动方程，水流运动方程式可按下式计算：

式中： 为综合系数； ， 为边界控制流量； 为单元网格尺寸； 为时间差；上标0为上次计算数值。

在计算过程中为提高计算结果的精度，考虑了计算中变量在每次计算中的变化，引入流速欠松弛因子系数，即将 引入方程中，因此最终的水流运动方程为：

进而使用动量插值，界面处的河道流量及修正流量按下式方程计算：

式中： 为水流运动方程矩阵综合系数；

计算中代入水流动量求解结果的流速值和水位值可求得流速初始值和上一层次的水位初始值，代入上述方程即可得到界面处的河道流量 ，再将 代入，修正后的水位可按下式方程计算：

式中：上标P为水位修正系数

在求得水位修正系数后，水位修正值及流速修正值可按下列方程计算：

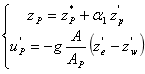
（3）结果检验

为了检验数学模型与计算过程的准确性及精度，选择典型年份的实测水文资料对数学模型进行率定与验证，并检验其精度。在计算过程中，主要对非恒定流的水位和流量过程进行验证。

验证计算的地形资料采用青戈江干流带状地形图及干流河道横断面资料。验证计算的水文资料采用2019年8月11日～8月13日的大砻坊、西河镇和清水河水文站的实测水位资料及实测流量资料进行验证计算。

由数学模型计算设计工况下流量和水位过程，与实测值比较，各测站水位过程的计算值和实测值基本一致，其误差一般在2cm之内，个别点达到8cm左右。模型计算的水位、流量过程基本符合实测成果，证明本次计算分析所采用的一维数学模型及计算过程在模拟河道水流运动方面有较高的可信度及精度。

5、结语

采用一维非恒定水流运动数学模型进行洪水的演进计算，计算结果与水文站实测资料进行对比表明本计算方法精度较高，根据模型计算成果，按照对防洪最不利的原则可拟定各河段设计流量，以供河流治理使用。本计算成果经验可为类似河道提供参考。