《分数除法》能不能这样上？——浅谈如何创新使用教材

《分数除法》能不能这样上？ —— 浅谈如何创新使用教材

聂蕾

济南市市中区育秀小学，山东 济南 250001

教学中经常会遇到学情与教材冲突的现象，此时就需要教师创新地使用教材，协调两者之间的关系，找到平衡点。0

“分数除法”一课，正是落实上述目标，推动学生“代数推理”能力的重要内容。它是在学生理解了分数的意义，学会了分数“加、减、乘”三则运算，掌握了求倒数的方法之后进行学习的。它作为代数部分的重要知识，处在除法这一运算所研究的最后的位置。算法并不难掌握，但算理却一直是教学的难点。在这之后面，它还对比和比例等内容提供知识经验和学习经验。所以在课程实施中，要重视概念的教学、算法的探索、算理的理解、数学思想方法的渗透，提高学生分析和解决问题的能力，增强学好数学的信心。

例1先利用平均分的意义，讲解一个数除以一个整数。那么 ÷2，就比较好理解，就是把 平均分成2份。但是到了 ÷3，得多少呢？孩子就糊涂了。

例2的题目是整数除以分数，可看出中间分析更繁琐。尤其是还有一次标准的变化，理解起来确实费劲。且不能像例1那样，用平均分的意义来思考。“是把2平均分成 份吗，把2平均分成3份取其中2份？”，很容易和2× 的意义混淆。

基于以上对课改方向和孩子学情的分析，我对这节课进行了如下处理。

1. 课例描述

1. 课前热身，埋伏“代数推理”方法。

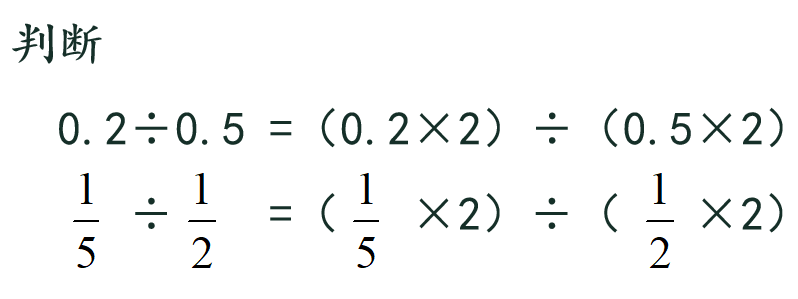
师：不计算，判断第1个式子对吗吗？为什么？

生：对啊。因为被除数和除数同时乘相同的数，商不变。

师：说得有理有据，再来看第2个，虽然大家没有学习分数除法，但是你能试着判断吗？说说你怎么想的。

生1：被除数只不过变成了分数，但是被除数和除数同时乘2，相同的数，商不变。

生2：老师，你看0.2就是 ，0.5就是_。那么第2题就是第1题的另一种形式。肯定一相等。所以第2个也对。

小结：也就是说商不变的性质，在分数里也适用。我们可以带着这个发现或者是疑问进一步学习。

【设计意图：这一环节是后面做代数推理的理论基础。这一环节的设计不仅是为了鼓励学生思考，更是为了后面的代数推理做铺垫，所以要及时的表扬孩子。同时再次丰富了转化的经验，所以设计了下面的过渡语，以此激发学生，提高学生的学习自信，落实增强学好数学信心的目的。】

师：同时我还特别佩服咱班同学，能利用我们学过的规律和性质，通过转化，有理有据的说明道理，可见转化在数学学习上是非常重要的。同时经过我们的推理，取得了新的发现，可见，转化和推理在数学的学习中都很重要。今天我们就要运用这两种思想学习新的内容。

2. 探究新知，熟悉“代数推理”方法。

新授课的第一个例题，我先讲解 ÷ 。就是求 包含几个 。分母相同，计数单位就相同，那么同分母分数相除就可以传化成直接将分子相除，也就转化成了整数除法。为了帮助孩子巩固这一认知，我又出了一题：

→

可总结计算方法，“同分母分数除法相除，直接用分子相除，得几商就是几”。出一组练习，及时巩固，同时处理掉 的问题。那就是_。

在以往的分数学习经验中，我们都是先研究同分母分数，再研究异分母分数，所以这里孩子应该可以猜到下面就开始研究异分母分数除法了。

【设计意图：这一部分的教学打破了教材的编排。借助原有整数除法的算理，推导同分母分数除法。当把整数看做是计数单位为 的分数，或者把分数转化成计数单位相同的整数时，除法的算理也就相通了，那么算法也就不难掌握了。关键是，这种统一并非老师硬塞的，还是学而生自然生成的。为此我利用学生以前认识分数的经验，先研究同分母分数，不仅做到了水到渠成，还很好的帮孩子理解，“计数单位相同，可以直接分子除以分”的道理。今天的学习就是对以往经验的再加工，训练的是学生“在加工”的能力，而这种能力就是“学习力”。】

第二个例题是 ÷ 。预设孩子能想到利用通分进行转化，如果不行就引导孩子转化。

“像比大小、加减法，我们是如何比较异分母分数的呢？”唤醒孩子的学习经验。

转化成同分母分数除法，统一计数单位，就可以继续除。以 ÷ 为例，它的通分过程是这样的： 。

被除数分子、分母要同时乘7，除数的分子、分母要同时乘5，这样就变成了同分母分数，计算方法是直接把分子相除。此时的分子变成了3×7和2×5，为了写成分数后好观察，我故意写成了3×7和5×2，结果就可以写成一个分式_。

【设计意图：这样的设计，符合了学习的“一致性”。每一步的学习都能借助前面的经验，新知识和旧知识不打架，而且例2的学习完全是建立在例1的基础之上，所以孩子掌握起来就更顺利。】

（三）突破难点，升级“代数推理”方法。

师：同学们，仔细观察，说说这样算合理吗？为什么？

生：我觉得行，因为被除数和除数同时乘了一个相同的数，结果还是一样的，不变的。

师：你是说商不变的性质在这里也适用。大家同意吗？

生：同意。

师：那我让被除数和除数同时乘个分数可以吗？

生：当然行啊。

师：那都乘 商会变吗？

生：（思考片刻）不变。

师：既然不变，那么会发生怎么的变化呢？（结合课件呈现）

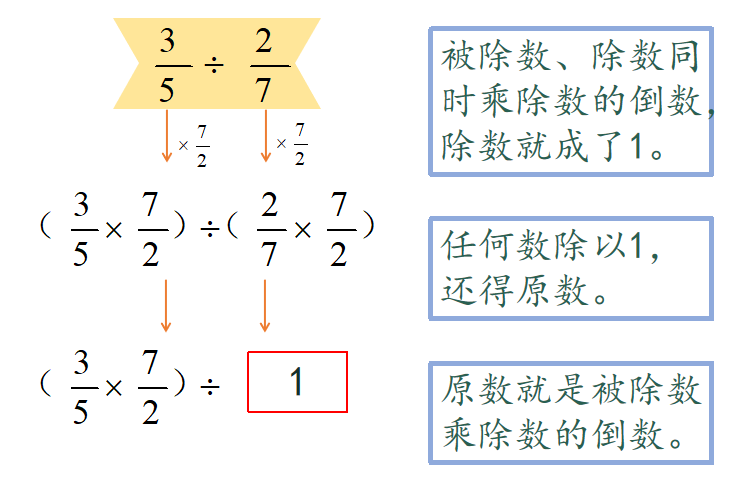
师：这下除数就变成了1，那不就是“任何数除以1，还得原数”吗。原数？就是这里的被除数乘除数倒数之后的数啊。

小结：“一个数除以一个非0的数，就等于乘这个数的倒数”。

师：明白了这个道理，我们就有两个方法了，通分和乘倒数。比较一下，你喜欢哪个啊？

生：当然是乘倒数啊，倒数多好找啊，分数除法计算不就能像乘法一样简单了吗。

师：那所有的异分母分数除法都可以吗？

生1：可以，谁还每个倒数啊。

生2：0没有

生1：不可能遇到0,0不能做除数。（孩子的思维震撼到了我。）

师：那这个方法适用于同分母分数除法吗？

生1：能，但是我还是喜欢直接除分子。

生2：我喜欢用这个。这个方法谁都能用，那还干嘛记两个方法啊，只要是除以分数，就乘它的倒数。

生3：两个方法不是更好吗……（不停的追问，引发孩子的思维碰撞。）

【设计意图：这部分学习让学生体会到代数推理的魅力，打通算法和算理间的壁垒。学生学习的整数除法、分数知识都用上了，实现了“掌握必要的运算技能”“运用数学的思维方式进行思考”“增强发现和提出问题的能力、分析和解决问题的能力”的目的。】

2. 课例反思

我们能做的就是给学习“造势”。就像脏桌子和抹布同时放在你面前，就会想拿起来擦一擦，如果你不想，那我就在旁边扫地。课堂上也是一样，学习材料都放在那里，如果这时还已经有人先动手解题了，那么大家的学习就会发生。我要做的就是帮学生唤醒“有用的”“有效的”经验。当所有知识经验、学习经验都放在他们眼前，他们自然能自己构建了。效率低课堂，多是负迁移和无效的内容太多。