核心素养观下小学数学试题编制策略

核心素养观下 小学数学试题编制策略

黄文丽

福建省古田县鹤塘中心小学

2021年，《小学数学课程标准修订版的大致变化》出台，给出了核心素养的定义。数学作为小学阶段的一门重要学科，数学核心素养相关的研究和实践层出不穷。数学素养是指运用数学知识、技能、态度解决数学真实问题的能力。修订版再次明确了“核心素养”包括关键能力和必备品格，并特别强调了“情感、态度、价值观”、思维与应用和过程性。目前评价学生的方式虽然多种多样，但书面试题测试仍是重要的评价手段，它具有发挥质量监测的评价导向功能。但试题编制工作还没引起足够重视。尝试从贴近生活，关注过程，倡导开放，融入文化，关注阅读等视角进行试题编制，以期达到培养学生数学素养的目的。

一、具体实际背景的问题设计，提高学生应用意识

我国古代数学巨著《九章算术》归纳出了若干解决生活中的实际数学问题的方法，它是数学与生活相结合的典范。生活中的很多问题都可以从数学的角度加以认识，当用数学的眼光来观察周围的世界时，往往发现有许多可以用于编制试题的素材。从生活中提炼出的新的素材，编制出背景为学生所熟悉的好试题，能够反映出命题者独到的眼光和深厚的数学功底。数学教师既要用数学的眼光和思维去观察社会，又要把丰富多彩的生活数学转化成学校数学，使之成为学生喜欢的数学试题内容。因此教师要做有心人，平时留意有价值的生活情境，积累素材，不必到需要时再花费大量时间和精力去收集。

2021年春节联欢晚会小品节目上有一个有趣的数学问题：

题1：果汁两元钱一瓶，两个瓶盖换一瓶，四个空瓶换一瓶，十元钱可以喝几瓶？

换购问题是生活中最常见的事例，计算一共可以喝几瓶这个问题是运用数学知识解决实际生活问题，体会数学在现实生活中应用的价值。解决这道题，首先要知道运用不同的规则，结果是不同的。不许借的话，就像春晚中郭冬临一样，最后一共喝到15瓶，还剩一个瓶盖和三个空瓶，解决这样的问题用图示的方法最为直观 。换一个方案，可以借的话还可以多喝5瓶。还有一种简便的计算（允许借的情况），每个盖子价值：2÷2＝1（元），每个空瓶价值：2÷4＝0.5（元），实际每瓶饮料：2－1－0.5＝0.5（元），10元钱最终可以喝到：10÷0.5＝20（瓶）。不管是画图还是计算的方法，学生都要用所学的数学知识去分析问题，解决问题，提高了用数学知识解决真实问题的能力，让学生认识到生活中蕴含有大量的数学问题，培养的学生的应用意识。

二、展示过程的问题设计，重视学生的思维过程

修订版《数学课程标准》再次强调了过程性，只要去做，必有收获。项目化也好，研究性也好，做出来的才是自己会的。评价不仅要关注获取知识的结果，更要关注知识的形成过程，引导教师设计探究题，让学生经历有过程的学习，关注知识的联系，促进知识的深刻理解，从而“知其然，也知其所以然”。

题2：求图中图形的面积，各种算法分别是怎样算的？用虚线表示出来。

5

5

12

8

8

55

12

10 10

（8+12）×10÷2-5×4÷2 10×8＋5×4÷2

5

5

12

8

8

55

12

10 10

8×5＋（8＋12）×5÷2 （10＋5）×8÷2＋12×5÷2

5

8

55

12

10

10×12－（5＋10）×4÷2

本题的设计不是要求仅仅会求组合图形的面积，而是力图全面暴露学生的思维过程，学生只有把每种算法与图形的组合方式相结合，才能准确的把虚线画出来，这样编题有助于了解学生的学习水平，及时发现学生在知识和思维上存在的问题，便于在今后的教学中对症下药。

三、开放性问题情境设计，培养学生的创造能力

单一指向的命题，只能培养单一的思维，不利于学生的发展。唯有包容“多向思维”，留给学生探索的空间和展现创造性思维的机会，学生的思维才能获得更多的发展，也更能调动学生学习的积极性，更加激发学生的探索兴趣，培养学生的创造能力。

1、逆向思维

事物都有它的两面性，换个角度思考，常常会有意想不到的效果，我们在设计试题时可以交换已知数与未知数的位置，使顺向思考的问题与逆向思考问题相互交换，这样常常会收到意想不到的效果。

题3:一个三角形的面积是24平方厘米，它的底和高（取整厘米数）分别是多少？（可以画图、列举，想出一种答案得满分，每增加一种答案，另加两分。）

这道题的改编的方法是改变呈现顺序，先出现面积，再求底和高，这就使学生必须回忆三角形面积的公式是怎么推导出来的。两个完全一样的三角形可以拼成一个平行四边形，这样拼出来的平行四边形的底和高与三角形的底和高是一样的，因此，求平行四边形的底和高也就求出了三角形的底和高，所以三角形的面积必须先乘2，得到平行四边形的面积，又由于三角形的底和高是取整厘米数，所以学生可以列举出所有的面积是24平方厘米的三角形，当然不是所有的学生都能把答案按顺序呈现出来，这也是为了满足试题创编的满意性原则，能给出一个答案，即可得分。答案呈现的越完整，得分越高。

2、增加条件

解决问题是培养学生应用意识和创新思维能力的重要途径，教师在设计应用题时，可适当的在题中增加一些相对多余的条件，以此启发，引导学生拓展思路，以提升发散思维与求异思维的能力。

题4：一本书一共140页，已经读了4/7，剩下的页数是已经读的几分之几？

其实这道题对于初学分数就解决实际问题的多数学生来说，直接画线段图非常容易理解，但一些学生不善于画图，列式（1- 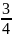） = 又过于抽象，不易接受，但有了“140页”这个条件，这些学生解题就容易多的。已读的：140× =80页，剩下的：140× =60页，60÷80=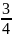 。这样做，虽然解题步骤相对复杂，但学生更容易理解。

3、减少条件

在解决问题过程中，如果条件不唯一，给学生提供多角度，多层次个性化的探索空间，更有利于学生发展创新意识。

题5：用一张长 40 厘米，宽 20 厘米的长方形铁皮，做一个深 5 厘米的长方体无盖铁盒。这个铁盒的容积是多少立方厘米？ （焊接处与铁皮的厚度不计）

本题看起来是求一个铁盒的容积，但是所提供的数学信息中没有明确地告知这个铁盒的长、宽、高分别是多少。学生要能够把文字信息转化为图形信息，再解决问题，所以考察的是学生的综合应用能力。

方法 1：长方形铁皮的 4 个角度各截去一个边长为 5 厘米的小正方形，然后折叠焊接成一个长方体。

铁盒的容积=30×10×5=1500 （立方厘米）

方法 2：从长方形铁皮中截取 4 个宽度 5 厘米、长度 20 厘米的小长方形，把这 4 个小长方形当作容器的四周，剩下的正方形当作底面，也可焊接成一个长方体。

铁盒的容积=20×20×5=2000 （立方厘米）。

方法 3：从长方形铁皮的左边上下两个角上各截取一个边长 5 厘米的小正方形，再把这 2 个小正方形移到铁皮的右边居中而放，刚好可折叠焊接成一个长方体如右图。

铁盒的容积=35×10×5=1750 （立方厘米）。

4. 融入数学文化问题，拓展学生的视野

数学是人类文化的重要组成部分，现行教材相当重视数学传统文化内容的渗透，试题编 制同样要依据教材把这些内容列入命题的范畴，关注文化性，让学生在考试中感受数学文化的渊源流长。

题:7：请你设计一个十六进制的计数器，你觉得个位至少需要几个珠子？

解决这个问题时，可以融入有关算盘的知识：我国传统的算盘，每档两个上珠，五个下珠，也称为七珠算盘，为什么有七珠呢？五珠不是就够了，原因是我国古代计算重量时采用的是十六两制，一斤等于十六两，现代人常说某两个人半斤八两，这是指他们彼此一样，不相上下。上二珠下五珠，每一档可计算到“15”，这样满“16”就向前一档进一，所以我国传统的七珠算盘是为适应十六进制而形成的。

4. 阅读分析的问题设计，考核学生获取信息能力。

数学阅读除了考查学生从一段文字中获取信息的能力，有时也考查学生从图表中获取信息的能力，甚至同时考查文字阅读和图表阅读，编制此类题目一般要结合学生具体的生活情境，让学生在具体情境中获取必要的信息，分析题目，进而解决问题。

小红参加夏令营活动。上面是他在网上查找到的厦门到北京的火车时刻表：

（1）青少年宫两位老师要带30名学生去北京参加“放飞少年中国梦,共学核心价值观念”主题活动，坐高铁G322列车比坐快速列车K572可以少用多长时间到达终点站？

（2）高铁G322从厦门北到北京南总行驶里程为2124公里，这列高铁平均每小时大约行多少公里？

（3）如果两位老师和30名学生都买快速列车硬卧票，一共需要多少元？（学生都超过1.5米，需买成人票。）

这道题以动车票为阅读情境，考查的是学生从动车票中获取信息的能力，动车票里面有不同列车的时间信息，有各种票价信息，要解决这道题的三个问题，学生不仅要分辨车票里面的各种信息，还要结合有关数学知识解决问题。在这个过程中，学生的数学综合能力得到提高，发展了学生的数学素养。

总之，小学数学试题编制工作一定要基于课标，重视数学素养的养成，只有这样，才能真正做到“教-学-评”的一致性，真正发挥评价的导向功能。