基于卡尔曼滤波的磁偶极子目标张量定位

基于卡尔曼滤波的磁偶极子目标张量定位

包 忠

中国船舶集团有限公司第七一○研究所，湖北 宜昌 443003

摘 要：针对现有单点磁梯度张量定位方法存在受测量噪声影响容易出现定位结果发散的不足，根据磁偶极子磁感应强度与磁场梯度张量的基本关系式，建立了张量定位的状态空间模型，并采用卡尔曼滤波器对状态向量进行估计，实现了目标定位。设计了数值算例对定位方法进行了检验，定位结果表明基于卡尔曼滤波的定位方法具有较高的精度和稳定性，可用于航空磁探测和水下小目标磁场探测。

关键词：张量定位；状态空间模型；卡尔曼滤波

水中铁磁物体，如钢铁航行体、水雷等，在地磁场的作用下会引起局部地磁异常，磁定位技术就是利用该磁异常信号来确定这些磁性目标的位置等参数^[1-3]。基于磁偶极子模型的磁性目标定位常见于航空探潜、水下地磁反演等领域。在航空探潜领域，通常先采用声探测技术来确定可疑海域，再用装载于飞机上的磁探仪接收到的潜艇磁场信号推算目标潜艇的运动要素及其与飞机的相对位置等参数，实现目标精确定位。

对适用于航空探潜的各种磁性目标定位方法，按采用的物理量来可以分为基于磁场总量^[4]、磁场分量^[5-7]和单点梯度张量^[8,9]等方法，其中单点梯度张量定位方法基于磁偶极子目标的线性探测方程，具有计算量小、实时性好的优点，一直以来是研究的热点^[8-10]。文献[8]对单点梯度张量定位方法进行了较为深入的研究，指出目标磁矩特征、测点与目标距离、磁探仪分辨率和磁梯度测量系统的基线距离是影响定位结果的四个主要因素，但却忽略了测量噪声对定位精度的影响分析。在航空探潜的实际工作中，磁场测量噪声不可避免地存在，其主要来源为测量系统噪声和飞机磁场干扰^[11]，这些测量噪声对定位结果具有重要影响。为此，本文以航空探潜和水下小目标磁场探测为应用背景，在考虑磁场测量噪声情况下，采用卡尔曼滤波理论对磁偶极子目标梯度张量定位进行研究，并设计了相应的仿真实验对方法的有效性进行验证。

1 目标定位数学模型

在卡尔曼滤波框架下，磁性目标张量定位的数学模型称为状态空间模型，状态空间模型由用于描述系统动态特性的状态模型和描述系统测量信息的量测模型两部分组成。

1.1 状态模型

状态模型的三个要素为状态变量，状态转移矩阵和状态噪声。构建状态模型的基本原则是所建立的状态模型既要符合系统动态特性实际，又要便于数据处理。在航空探潜过程中或小目标磁场探测中，传感器平台的位置、速度和姿态一般由平台的导航系统提供，为已知量，在进行张量定位方法分析时可假定测量平台静止而目标运动，如图1所示，其中坐标系原点o为探测系统的中心，x轴，y轴和z轴分别平行于地磁坐标系相应的三轴。

由于探测过程持续时间较短，一般假定在定位过程中潜艇目标作深度不变的匀速直线运动^[10,12-13]。此时，可采用目标在水平方面航速v_x，v_y以及目标与探测系统的相对位置r来描述其运动过程的动态特性，即可定义状态变量x=(x,y,z,v_x,v_y)^T，则：

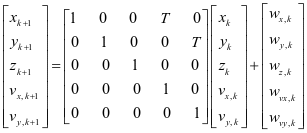（1）

式中T为测量设备采样周期，k=0,1,2,…N为采样时刻。上式写成矩阵的形式为x_k+1=A_k,k-1x_k+w_k，其中A_k,k-1称为状态转移矩阵，状态噪声w_k=(w_x,k,w_y,k,w_z,k,w_vx,k,w_vy,k)^T为相互独立的高斯白噪声，其方差为R。

图1 目标张量定位示意图

1.2 量测模型

磁偶极子是磁性目标定位中使用最为广泛且最有效的数学模型。对位于源点S的磁偶极子，其空间中任意场点P处的磁感应强度B(B_x,B_y,B_z)可按下式计算：

（2）

式中：r为由源点S指向场点P的位置矢量，m为磁偶极子磁矩，μ为介质磁导率。

磁感应强度的三个分量(B_x,B_y,B_z)在空间三个方向(x,y,z)的变化率构成一个张量矩阵G=[G_ij]_3×3，G_ij的表达式如下：

（3）

式中：i,j=1,2,3；B₁，B₂和B₃分别表示磁感应强度的三个分量B_x，B_y和B_z；r₁，r₂和r₃分别表示矢径r的三个分量r_x，r_y和r_z；δ_ij为Kronecker-Delta函数。

由文献[8,9]，磁偶极子磁场梯度张量与磁场的关系为：

（4）

在磁偶极子目标定位实际工程中，目标磁场一般采用精度较高的超导量子磁力仪进行测量，其测量精度可达到pT级，磁场测量值中包含目标磁场真值、地磁噪声和载体干扰磁场等。磁场梯度张量可采用5个三轴磁传感器^[9]或10个单轴磁传感器^[14]的输出经差分后得到，该测量方式极大地降低了同模测量噪声的干扰，因此可认为梯度张量测量值即为目标梯度张量真值。为此，观测方程可写为：

（5）

其中Y_k和x_k分别表示k时刻的观测值（磁场测量值）和状态向量；v_k为k时刻的测量噪声，一般认为其为方差为Q的高斯白噪声；H_k为观测矩阵，具体表达式为：

（6）

此外，在估计得到目标与探测系统的相对位置后，可采用式（7）计算目标磁矩参数，该参数可用于目标的分类识别。

（7）

1.3 可观测性分析

采用卡尔曼滤波求解式（1）和式（5）描述的磁性目标定位模型的前提是定位模型可观测。由线性系统理论，可采用如下的观测性矩阵Q_o来分析其可观测性：

（8）

若Q_o矩阵的秩大于等于待观测向量维数，则系统可观测。将H，A代入上式后，取Q_o阵的某一6阶子阵如下：

， （9）

明显，若||G||≠0，则TG至少存在一个行列式不为零的2阶子阵；从而Q_o1至少存在一个行列式不为零的5阶子阵，即若||G||≠0，系统可观测。

2 卡尔曼滤波基本原理

卡尔曼滤波是一种线性最小方差统计估算方法，它是通过处理一系列带有误差的实际测量数据而得到物理参数的最佳估计。其实质是以预测方程和测量方程为基础，用递推的方法计算系统状态变量x_k的最小均方估计值 。对于式（1）和式（5）描述的状态空间模型，其递推公式为：

状态预测： (10)

方差预测： (11)

增益计算： (12)

状态估计： (13)

方差更新： (14)

给定初值x₀和P₀后，根据k时刻（k=1，2，…）的观测值Y_k，就可以递推计算得k时刻状态的最小均方估计值 。

3 数值算例分析

采用与文献[9]中类似的数值算例来检验本定位方法的有效性，数值算例各参数具体取值见表1。

表1 数值算例参数

卡尔曼滤波迭代起始点x₀由相对位置和水平方向的速度两部分组成，其中相位位置可通过直接求解式（4）得到，而在迭代起始时刻的速度是无法获知的，因此取速度的两个分量为0。P₀随着递推的进行，将较快收敛，因此实际使用时，P₀可以取得稍大一些。在该算例中取P₀=diag(10m,10m,10m,5m/s, 5m/s)。

分析步骤为：①假设目标与探测系统的相对速度v_x=3m/s和v_y=1m/s，由采样周期和探测线L计算各采样时刻目标与探测系统的相对位置（记为理论值）；由相对位置和磁偶极子磁矩按式（2）计算各采样时刻的磁场感应强度，并由文献[9]中方法计算相应的目标磁场梯度张量；②分别采用文献[9]中的直接计算法（记为直接计算值）和本文的卡尔曼滤波方法计算目标位置（记为卡尔曼滤波值）并按式（7）计算相应的目标磁矩；③比较相对位置和磁矩的直接计算值、卡尔曼滤波值与理论值，结果见图2和图3。

图2 定位结果比较图

图3 磁矩参数计算结果

从图中可以看出，磁场测量噪声的存在导致直接计算的位置参数具有较大的振荡，相应的磁矩参数计算结果也具有较大的振荡，说明直接计算的稳定性较差。而采用卡尔曼滤波得到的位置参数和磁矩参数在滤波器收敛后，能有效克服测量噪声对位置参数计算的影响，具有较强的稳定性，且设计的滤波器具有较快的收敛速度。

本文在磁偶极子模型的基础上，建立了适用于磁梯度张量定位的状态空间模型。在目标磁感应强度测量不可避免地存在测量噪声的实际情况下，采用卡尔曼滤波对模型进行了求解。设计了相应的数值算例，计算结果表明基于卡尔曼滤波的定位方法具有较高的定位精度和较强的稳定性。该研究工作对航空磁探测和水下小目标磁场探测，都具有一定的指导意义。

参考文献

[1] Tarek El Tobely, Ahmed Salem. Position Detect ion of Unexploded Ordnance from Airborne Magnetic Anomaly Data Using 3-D Self Organized Feature Map[J]. International symposium on signal processing and information technology, 2005: 322-327.

[2] 徐杰. 一种高效的舰船磁性定位方法[J]. 舰船科学技术,2011,3(12):69-71.

[3] 唐莉莉, 宋勇, 童官军,等.一种新的运动磁目标定位算法[J]. 传感技术学报,2011,24(7): 996 -1000.

[4] Xiao Changhan, Liu Shengdao , Zhou Guohua. Rea-l time localization o f a magnetic object with total field data[ M].US: IEEE, 2008.

[5] 李华, 李庆民, 龚沈光,等.基于磁性目标磁场模型的在线磁定位研究[J]. 武汉理工大学学报(交通科学与工程版).).2009,33(1):165-168.

[6] 黄玉, 郝燕玲.水下地磁异常反演中位置磁矩联合迭代算法[J]. 华中科技大学学报(自然科学

版),2011,39(7):95-98.

[7] 赵文春, 刘大明, 周国华. 基于微分进化算法的磁性目标参数估计方法[J]. 舰船电子工程, 2011,

31(167):167-170.

[8] 肖昌汉, 何华辉. 磁性物体探测的线性求解方法[J]. 华中理工大学学报,1997,25(4):83-85

[9] 张朝阳, 肖昌汉, 闫辉. 磁性目标单点梯度张量定位方法[J]. 探测与控制学报,2009,31(4): 44-48.

[10] 王光源, 马海洋, 章尧卿. 航空磁探仪探潜目标磁梯度定位方法[J]. 兵工自动化,2011,30(1):32-34.

[11] 谭斌, 林春生, 张宁. 地磁场梯度对飞机磁场求解精度的影响分析[J]. 武汉大学学报(信息科学版), 2011,36(12):1482-1485.

[12] 李居伟, 徐以成, 孙明太. 航空磁探仪目标运动分析仿真研究[J]. 指挥控制与仿真,2011,33(4):72-74.

[13] Marius Birsan. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer[J]. IEEE Transactions on Magnetics,2011,47(2):409-415．

[14] 黄玉, 郝燕玲. 磁场梯度张量定位中的矢量磁力计最简配置[J]. 华中科技大学学报(自然科学版),

2010,38(12):52-55.