长安大学,陕西西安, 710061
摘要:随着近年来全球变暖,火山活动频繁,自然灾害增多,例如飓风,地震等灾害毁坏房屋的事件时有发生,而目前的救灾机器人大多是采用履带式结构,不能很好的完成在复杂地形之上的任务。研究采用D-H法,蒙特卡洛法等方法,并利用MATLAB,CATIA等软件为工具,构建单腿柱状结构模型,并求出单腿足端在六足本体坐标系下的空间位置矩阵,和各单腿的足端在六足本体坐标系下的空间位置,最后在MATLAB平台中绘制本研究六足机器人腿5的足端的工作空间以及各个二位平面图上的空间范围,最后优化了六足机器人在复杂地形情况的步态运动规划,提升了六足机器人在复杂地形情况下运动的能力。
关键词:六足机器人;复杂地形情况;步态规划
引言
近年来,随着全球变暖,火山活动频繁,地震海啸频发,给人民的生命财产安全带来巨大挑战。目前救灾主要依靠人工和大型工程机械进行外部作业,而小型的救灾机器人,主要进行进入废墟内部进行被困人员。目前机器人均采用的是履带式,在复杂情况下,诸如陡坡等情况容易发生事故。而六足机器人的腿拥有较多的自由度,因此其在运动的过程中较为灵活,而且与轮式和履带式机器人相比较,足式机器人与地面的接触面积更小,故而在崎岖不平的地面上更容易找到合适的支撑点。但是,六足机器人的步态研究仅限于如何在平整地面上行走加速,对于复杂地形情况下的步态研究关注相对较少。例如南京理工大学的李桂海对全气动多自由度关节型机器人平稳步态进行了研究,
浙江工业大学的郭锦涛便提出了一种新型的多自由度关节机器人在平稳步态的研究。
基于此,本研究将着重于六足机器人的步距计算,以及六足机器人在复杂地形情况下的步态规划。
六足机器人的步距计算
在机器人的运动分析中,在一个步态周期中与地面接触的各条腿称为支撑相,脱离地面的各条腿称为摆动相,在一个步态周期T中,假设支撑相所用的时间为 ,摆动相所用的时间为
,摆动相所用的时间为 ,则占空比
,则占空比

再设支撑相的足端的速度为 ,本体移动速度为
,本体移动速度为 , 摆动相的足端的速度为
, 摆动相的足端的速度为
步行腿从摆动相到支撑相的位置称为前极限位置(AEP),支撑相到摆动相的位置称为后极限位置(AEP)。
支撑相的足端的速度为:

摆动相的足端的速度为:

当机器人行进时,支撑相的腿数为u,摆动相的腿数为n-u时称为u足步态,参数u与占空比 的关系式为:
的关系式为:
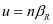
因为 ,所以
,所以

所以步距S为:

在式中代入以下的参数:
机器人的要求速度 、步态周期为
、步态周期为
求得机器人的步距为:
步距是前极限位置与后极限位置之间的距离,如图其中单腿从摆动相到支撑相的位置称为前极限位置(AEP),从支撑相到摆动相的位置称为后极限位置(PEP)。

六足机器人的单腿工作空间
D-H方法首先在六足机器人本体的中心位置以及单退的每个关节处建立一个坐标系,然后通过齐次坐标变换来实现两个关节坐标的变化。在多关节串联的系统中多次使用齐次坐标变换就可以建立首末坐标系的关系。D-H方法包含四个运动学参数,其中两个参数用来描述连杆本身,另两个参数用于描述连杆之间的关系,这四个参数分别为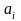 、
、 、
、 、
、 ,其中,
,其中,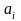 表示沿着
表示沿着 轴,从
轴,从 移动到
移动到 的距离;
的距离; 表示沿着
表示沿着 轴,从
轴,从 旋转到的
旋转到的 的角度;
的角度; 表示沿着
表示沿着 轴,从
轴,从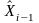 移动到
移动到 的距离;
的距离; 表示沿着
表示沿着 轴,从
轴,从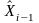 移动到
移动到 的角度。对于一个新的机构,通常按照以下步骤正确建立D-H[23]坐标系:1)找出各关节轴,并标出或画出这些轴线的延长线;2)找出关节轴i和i+1之间的公垂线或者关节轴i和i+1之间的交点,以关节轴i和i+1之间的公垂线或者关节轴i和i+1之间的交点作为连杆坐标系{i}的原点;3)规定
的角度。对于一个新的机构,通常按照以下步骤正确建立D-H[23]坐标系:1)找出各关节轴,并标出或画出这些轴线的延长线;2)找出关节轴i和i+1之间的公垂线或者关节轴i和i+1之间的交点,以关节轴i和i+1之间的公垂线或者关节轴i和i+1之间的交点作为连杆坐标系{i}的原点;3)规定 轴沿关节轴i的指向;4)规定
轴沿关节轴i的指向;4)规定 轴沿公垂线的指向,如果关节轴i和i+1相交,则规定
轴沿公垂线的指向,如果关节轴i和i+1相交,则规定 垂直于关节轴i和i+1所在的平面;5)按照右手定则确定
垂直于关节轴i和i+1所在的平面;5)按照右手定则确定 轴;6)当地一个关节变量为零时,规定坐标系{0}与坐标系{1}重合,对于末端坐标系{n},其原点和
轴;6)当地一个关节变量为零时,规定坐标系{0}与坐标系{1}重合,对于末端坐标系{n},其原点和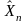 的方向可以任意选取,但是在选取时,应尽量使连杆参数为0。
的方向可以任意选取,但是在选取时,应尽量使连杆参数为0。
基于六足机器人的单腿5的D-H运动学模型参数


图3.3Robotics Toolbox工具箱建立的单腿模型
可得各关节的坐标变换矩阵如下:




其中单腿5的足端在六足本体坐标系中的位置为:




单腿5的足端在六足本体坐标系中z的方向矢量:




根据整体结构设计可得各项参数值为:
 ,
, ,
, ,
, ,
, ,
,
所以单腿5的足端在六足本体坐标系中的位置为:



借助Robotics Toolbox工具箱绘制本研究六足机器人单腿5的腿端工作空间如图 

由上图可知本研究的六足机器人的单腿的足端工作空间云图分布较为均匀,在云图中间未出现明显的空洞,这表明本研究六足机器人的足端可以按照设计的理想需要的到达各个需要的位置,由三维图可知本研究六足机器人单腿的足端工作空间所到达的位置点的集合像是一个偏扇形的椭球外壳形状,其具体的工作空间范围为:0mm
单腿摆动相的足端轨迹规划
根据本研究六足机器人的设计要求和整体结构设计,我们可以设定六足机器人单个腿部运动的开始时间 =0s,中间时间
=0s,中间时间 =0.5s,以及终止时间
=0.5s,以及终止时间 =1s,并且可根据MATLAB中的机器人工具箱Robotics Toolbox所构建的单腿5的关节模型 ,获得摆动相的起始位置,停止位置和中间位置,并且根据已知条件可得起止位置的的速度和加速度,这样本小节可获得七个约束条件,如此一来,本小节将摆动相的曲线轨迹方程设为一个六次多项式函数,并利用上述七个约束条件便可求解出摆动相的具体的曲线轨迹方程。
=1s,并且可根据MATLAB中的机器人工具箱Robotics Toolbox所构建的单腿5的关节模型 ,获得摆动相的起始位置,停止位置和中间位置,并且根据已知条件可得起止位置的的速度和加速度,这样本小节可获得七个约束条件,如此一来,本小节将摆动相的曲线轨迹方程设为一个六次多项式函数,并利用上述七个约束条件便可求解出摆动相的具体的曲线轨迹方程。
代入已知的七个约束条件的数值联立方程可求得本研究的六足机器人单腿的摆动相足端的轨迹曲线方程为:


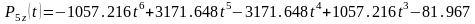

(利用MATLAB软件绘制本研究的六足机器人单腿的摆动相足端的速度轨迹曲线)

(六足机器人的摆动相单腿足端的三方向的加速度轨迹曲线图)
如上图可知本研究的六足机器人的加速度轨迹曲线过渡完美,没有出现断点或者斜率突变的情况,且三个方向上的速度在一个周期内的起止时刻的值均为零,完美的满足了约束条件,因此所求的速度轨迹曲线方程满足设计要求,可较为清楚的反映出本研究的六足机器人在一个步态周期内的各个方向上的加速度变化情况。
六足机器人的三足步态运动规划
六足机器人有多种行走步态,比如与慢波步态、四足步态和三足步态,本研究的研究采用经典三足步态,因为同其他步态相比,三足步态的姿势较快的行走会使机器人自发采取更多更高的位置,行走一般更稳定;因此本研究首先将六足机器人的六条腿分为两组,将1,2,3腿分为一组,将之称为六足机器人的左侧腿,4,5,6腿分为一组,将之称为六足机器人的右侧腿,并使用CAITA平台中的数字化装配模块模拟出六足机器人的基本运动姿态,从而得到详细的步态分解过程图,本次设计中为六足机器人设计了三种不同高度的行走姿态,分别为低位姿态、中位姿态和高位姿态,不同的姿态位置影响了摄像头的视野范围,在未来可根据实际需要的视野范围来选择不同的姿态。
在三种姿态下的基本动作方式的动作过程基本一致,接下来本小节以低位姿态的基本动作方式的动作过程为例对步态过程进行详细的分解如下所示:
(1)前后进
第一步:1、3、5腿抬起第二步:1、3、5腿前移第三步:1、3、5腿放下



第四步:2、4、6腿抬起第五步:1、3、5腿归位第六步:2、4、6腿前移



第七步:2、4、6腿放下 第八步:1、3、5腿抬起 第九步:2、4、6腿归位



(3)左右转:
第一步:1、3、5腿抬起第二步:1、3、5腿逆时针旋第三步:1、3、5腿放下



第四步:2、4、6腿抬起第五步:1、3、5腿归位第六步:2、4、6腿逆时针旋转



第七步:2、4、6腿放下第八步:1、3、5腿抬起第九步:2、4、6腿归位



根据以上的基本动作分解图可知,每个大的动作均由九个阶段的小动作组成,而且在运动的过程中,本研究的六足机器人的六条腿以腿1、3、5和腿2、4、6分为了两组,同组腿的运动状态是一样的,它们保持同步的抬起,旋转和放下的动作。且由上述图示可知在本研究六足机器人的运动过程中,总有三条腿与地面接触,围成三角形的形状以保证本研究六足机器人在运动过程中的稳定性。
结语
本研究在复杂地形情况下步态设计过程中,首先通过MATLAB平台中的机器人工具箱计算出了六足机器人的单腿足端工作空间,并用点图的形式表现出来,然后采用多项式插值法根据已知的轨迹条件求解出六足机器人的足端的位置轨迹方程,求解出了六足机器人摆动相和支撑相各自的轨迹、速度和加速度的曲线方程,并借助MATLAB平台绘制出了方程的轨迹曲线,根据方程曲线的光滑程度验证了步态轨迹规划的合理性,最后借助于CATIA平台对六足机器人的进行了三维建模,采用三足步态对六足机器人进行了步态分解,详细阐述了六足机器人在复杂地形情况下的步态,理论上适合六足机器人在复杂地形情况下使用。
参考文献
陈甫.六足仿生机器人的研制及其运动规划研究.[D]. 哈尔滨:哈尔滨工业大学 [博士学位论文].2009
宣奇波.多足步行机器人步态规划及控制系统的研究.[D].杭州:杭州电子科技大学 [硕士学位论文].2013
王志英. 径向对称六轮腿月球机器人步态规划[D]. 北京:北京航空航天大学[博士学位论文].2010
王倩. 六足仿生器人步态规划与控制系统研制[D]. 哈尔滨:哈尔滨工业大学[硕士学位论文]. 2007:1-9
【项目基金】:“挑战杯”重点资助项目:《基于视觉感知的搜救六足机器人》,项目编号:A-IA-B-11
【第一作者简介】:凌培杰(2000.05-),男,汉族,江苏省无锡市,本科在读,机械设计制造及其自动化研究方向;
【*通讯作者】:封硕(1987),男,汉族,陕西省西安市,长安大学工程机械学院,副教授/博士,智能制造。