学生的错误，考验教师的智慧

学生的错误，考验教师的智慧

王东升 [1] 张贺 [2]

辽宁省阜新市教育服务中心 123000 辽宁省阜新市第一中 123000

【摘要】 学习的过程就是一个渐进的、试误的过程，可以说没有错误就没有真正意义上的学习。每位教师都应该善待学生的错误，并善加利用，使教学走向深入，使教育走向人本。

【关键词】 学生的错误 教师的智慧 教学机智 个性创新

引言

在课堂教学中，学生出错是常有的事，而同时教师的解决方式也各不相同，效果也自然天差地别。是冷眼旁观，还是耐心引导？是恶语相讥，还是保护个性？是嗤之以鼻，还是鼓励创新？如何对待学生的错误（也许不是错误，只是想法新奇），是每个教师必须正视、回答的问题。本文以一节复习课的片段为例，谈谈笔者的思考。

【案例】

这是一节一元二次方程解法的复习课。其中有一道练习题是这样的：

解一元二次方程 .

多数学生都能较好地完成此题，只是熟练程度有别,方法选择各异。我身边的学生小明（匿名）是这样解的：

解：

，或

所以， .

当王老师（匿名）巡视到小明身边时，看了看他的解答，冷冷地说：“错了，用公式法或者配方法再解一遍”。小明垂头丧气地重新用公式法解了一遍。得出了正确的结果： 。

一切归于平静，教学在继续。但是，我却平静不下来。课后，我找到了王老师。

我：王老师，您想过学生为什么会出现这种错误吗？

王老师：没有。

我：学生是否有办法判断自己的解是错误的？

王老师：没想过。

我：学生的做法中是否有合理成分呢？

王老师：有吗？

课后，我也找到了学生小明。

我：小明，你这样解一元二次方程，是怎么想的？

小明：我是利用因式分解方法，这是提公因式啊！

我：老师在讲因式分解法解一元二次方程时，要求左边是整式的乘积，右边是零，你的做法也不符合这个要求啊！

小明：为什么要求等式右边必须是零呢？x比（x+5）小5，1比6也小5。小乘以大等于小乘以大，等式左边较小的应该等于等式右边较小的，左边较大的也应该等于右边较大的。

我：王老师说你写错了，你当时有什么想法？

小明：王老师说我错了，那我肯定错了。后来我用公式法得出的结果也说明我错了，可是，我就是不明白错在哪儿了。我的想法挺合理的呀？！

【分析】

从访问的对话可以看出，学生不知道为什么会错，教师也不知道学生是怎么想的，最后的结局就是，学生的错误认识没有能够得到及时的纠正，学生新奇的想法也没有得到充分的挖掘。教师的做法再次强化课堂上的一个法则：学生只要按照老师教的方法解题就可以了，不要有什么古怪的想法。

可以明显看出，学生小明的思考是不够全面的。小明没有考虑到相差为5乘积为6（前小后大）的两数乘积，既可以是 也可以是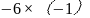 .所以，可以按照小明的思路把解答过程修改如下：

解：

，或

所以， .

这与正确答案完全一致！如此看来，小明的思考是有他的合理性的！

事实上，这种思想方法在解决满足特定条件的等式问题时常有应用。

例1 求方程 的正整数解。

解：由题意，得 .

因为 ， 是正整数，则 ，于是可组成下面的方程组：

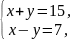
解方程组，得

深入思考之后我们会发现，学生小明的解题根据是“当 ，且 时，有 ， ”，即为命题“ ”。那么，这个命题是正确的吗？探索如下：

解：因为 ,所以 .

所以 .

所以 .

（1）当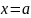 时，由已知 即 ，命题成立.

（2）当 时，由已知 即 所以 因为 所以 .

即正确命题为：“ ”。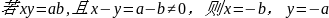

我们惊喜的看到，小明的思考虽有偏差，但是蕴含着与数学原理相合的成分，这对于一个初中生来说是多么的难能可贵呀：朴素的直觉，勇敢的发现，创新的萌芽！然而，就因为他的解法不和“常法”，却被老师无情的忽略了。

用“小明的解法”再来解一个稍复杂的一元二次方程。

例2 解方程 （二次项系数不为1）.

解：

，或

所以， .

到此，我们似乎可以得到结论：能用十字相乘法解的一元二次方程，都可以用“小明的解法”来解。并且，在常数项分解的思考环节，比常规的十字相乘法还要容易一些，这恰恰可以解决“用十字相乘法解一元二次方程”的教学难点。

特别情况下“小明的解法”更有优势！比如下例：

例3 解方程 .

解：

,或

所以， .

按照一般的解法，需要将方程中的因式相乘，合并整理后再求解。而“小明的解法”却可省去这个环节，使解题过程更简捷。

【启示】

英国心理学家桑代克说过，学习的过程就是一个渐进的、尝试错误的过程。可以说没有错误就没有真正意义上的学习。在前文所述的案例中，从学生出错到教师的应对，带给我们的有惋惜，也有思考：老师是在用行动回答：你是学生可信赖的“平等的导师”吗？

1. 善待学生的错误。

学生数学学习的过程不能单纯的依靠模仿和记忆，而是建立在经验基础上的一个主动建构的过程，这个过程充满了观察、实验、猜想、验证、推理与交流等丰富多彩的数学活动，教师要允许学生在这个过程中出现不同错误，并以引导帮助学生化解各类错误为己任，教师要科学诊断，耐心倾听其发表自己的观点，引导学生自己去分析，并寻求正确的结论或较佳的解决问题的方案，促使学生在学习数学的过程中获得自信和更多的成就感。

比如案例中的王老师，在发现小明的出错后，如果能耐心的了解小明的想法，帮助小明确认自己的答案为什么是错误的，理清小明导致解题错误的原因，纠正小明想法中的错误，相信会给小明带来完全不同的体验。

2. 鼓励学生的个性创新。

从某种意义上讲,教学是教师个性与学生个性相互影响的过程。传统学科教学,偏重于共性的要求,而忽视个性的培养,这样往往导致学生主体性,能动性,独立性的不断消失,从而影响学生创新能力的培养。对教师而言,必须从心底里乐于接受学生提出的不同观点和意见。教师只有在课堂上与学生真正地进行了思想和情感的交流, 尊重个性发展，鼓励求异创新，才能给予学生可感知的理性精神的熏陶,课堂教学才能真正成为“教学相长”的过程。

比如案例中的王老师，如果能够发现小明错误解答中的合理成分，纠正小明想法中的偏差，鼓励小明善于思考的学习态度和敢于探索的科学精神，无疑会给小明在数学学习和创新思维的道路上带来极大的鼓舞。

3. 学生的错误也是教学资源。

在学习过程中学生出现错误时，教师要让学生充分展示自己的思维过程，从中发现合理的成分和闪光点，给予肯定和欣赏，并顺着学生的思路，引导他们通过各种形式的探究活动,寻找错误原因，得出解决这类问题的方法。教师不但可以通过挖掘学生的错误资源,及时调整课堂教学,还可以利用学生的错误资源,引导学生主动探究。

比如案例中的王老师，如果能够利用小明错误，组织同学们互助研讨，积极探索，最后形成“新解法”，让学生经历直觉感知，大胆猜想，比较分析，归纳概括，理性抽象的过程，让学生享受这个真正的学习过程！这是一段多么令人难忘的数学经历呀：有困惑，有收获；有思考，有交流；有规则，有创新；有通法，有个性；有深度，有温度。

4. 提高课堂教学机智。

教学机智是教师在课堂教学中面对突发事件，迅速、准确的做出判断，处理并维持教学的一种能力。这需要教师要有敏锐的观察能力、灵活的调适能力等。在课堂教学中，教学机智常常表现为，教师能否充分利用一切有利于教学的信息，比如说学生的发言、学生的评价、学生的错误，引导学生发展；能否针对课堂教学中的偶发事件，临时改变教学策略与手段，保证教学的顺利进行。

教学机智源于教师对教育的真正理解，对学生成长的真心关怀。有时表现的只是克制，只是对学生体验的理解，只是对学生主体性的尊重，教学机智能对意想不到的情境进行崭新的塑造，使小事变得有意义，使教学行为充满智慧^[1]。作为一名教师，要自觉地反思自己的教学行为，不断地提高教育感知力。

【参考文献】

[1]马克斯·范梅南. 教学机智:教育智慧的意蕴:the meaning of pedagogical thoughtfulness[M]. 教育科学出版社, 2001.

[2]王鹤新. 学生的"错误",更考验教师的教学智慧[J]. 物理教学, 2014(36):10-12.

[3]康世刚. 读懂学生的错误是卓越教师必备的智慧[J]. 今日教育, 2013(5):51-51.

[4]韩四清. 慧眼识金 机智引渡——对待错误,教师应有的智慧与气度[J]. 教育实践与研究(小学版), 2009.

[5]韩瑞仕, 高丽. 用心浇花花更艳--一个问题生的蜕变[J]. 都市家教(下半月), 2013(10):242-243.