《二次函数与图形面积》教学设计

《二次函数与图形面积》教学设计

王显翠

湖北省十堰市郧阳区高庙九年一贯制学校 湖北十堰 442518

【题源1】：（人教版教材九年级上册P49页探究1）用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化.当l是多少时，场地的面积S最大？

【题源2】：（人教版教材九年级上册P57页XT7）如图1，用一段长为30m的

篱笆围成一个一边靠墙的矩形菜地，墙长18m，这个矩形的长宽各是多少时

，菜园的面积最大、最大面积时多少？

【设计思路】：在周长一定的情况下，矩形的面积最大时时正方形，每个边长占四分之一，如探究1中的结论;在习题中由于一边靠墙，面积最大时并不是正方形，而是平行与墙的一边占篱笆一半。那么改变墙的长度，能否达到这种效果呢?如果可以的话，三面篱笆就应该各占三分之一，并且题目中说“一边靠墙”，那么靠墙的这一边是以墙长为一边还是一边的一部分?为此，在设计这节探究课的过程中，把墙的长度设置在“篱笆的三分之一以内”，“三分之一与一半之间”及“大于篱笆的一半”三种情况;分“墙长一部分为一边”和“墙为一边的一部分”两类分别计算。

【过程设计】：

一复习导入

1，下列抛物线的开口方向、对称轴和顶点坐标，并写出其最值.

（1）y=x²-4x-5; (配方法) (2)y=-x²-3x+4.(公式法)

2， 从地面竖直向上抛出一小球，小球的高度 h（单位：m）与小球的运动时间 t（单位：s）之间的关系式是h= 30t - 5t ² （0≤t ≤6）．小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？

二、探究新知

用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l

的变化而变化.当l是多少时，场地的面积S最大？

解：根据题意得

S＝l(30－l)＝－l²＋30l.( 0＜l＜30）

因此，当l=- S有最大值也就是说，当l是15m时，场地的面积最大。

【变式1】： 如图1，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长32m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

问题1 变式1与例题有什么不同？如何设自变量？ 问题2 面积S的函数关系式是什么？

问题3 如何求解自变量x的取值范围？墙长32m对此题有什么作用？

【变式2】 如图1，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

问题1 变式2与变式1有什么异同？ 问题2 可否模仿变式1设未知数、列函数关系式？

问题3 可否试设与墙平行的一边为x米？则如何表示另一边？

问题4 当x=30时，S取最大值，此结论是否正确？

实际问题中求解二次函数最值问题，不一定都取图象顶点处，要根据自变量的取值范围.通过变式1与变式2的对比，希望同学们能够理解函数图象的顶点、端点与最值的关系，以及何时取顶点处、何时取端点处才有符合实际的最值.

【变式3】：用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长am，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

解题分析：在变式1、2中都给定了图1这样的具体图形，如果没有具体图形应该还有图2这种情况 ，何时面积最大，就要通过计算作以比较

解:设平行与墙的一边为xm

(1)当0＜a＜20时（如a =16）

①以墙的一部分为一边，则（如图1） = =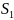

∵0＜X≤16且 ∴当X=19时，

②以墙为一边的一部分，则（如图2） = =

∵16≤X＜38且 ∴当X=16时，

∵ ∴此时当长和宽均为19m是菜园面积最大，最大面积为361 的正方形，

推而广之，当0＜a＜20时，以墙为边长的一部分围成的矩形面积最大，是边上为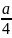（ + ）m, 最大面积为（ 的正方形

(2)当20≤a≤30时（如a =24）

①以墙的一部分为一边，则（如图1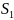） = = ∵0＜X≤24且 ∴当X=24时，

②以墙为一边的一部分，则（如图2） = =

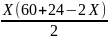∵24≤X＜42且 ∴当X=24时，

∵ ∴此时当长24m,宽为18m是菜园面积最大，最大面积为432 的矩形，

推而广之，当20≤a≤30时，两种情况面积一样大，是长为a m，宽为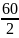（ - ）m, 最大面积为（ 的矩形。

(3)当30＜a＜60时（如a =40）

①以墙的一部分为一边，则（如图1）

= =

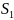∵0＜X≤40且 ∴当X=30时，

②以墙为一边的一部分，则（如图2） = =

∵40≤X＜50且 ∴当X=25时，

∵ ∴此时当长30m和宽均为15m是菜园面积最大，最大面积为450 的矩形，

推而广之，当30＜a＜60时，以墙的一部分为边围成的矩形面积最大，是长为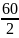 m，宽为 m, 最大面积为450 的矩形。

(4)当a 60时（如a =60）

①以墙的一部分为一边，则（如图1） = =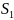

∵0＜X≤60且 ∴当X=30时，

②以墙为一边的一部分，则（如图2）

∵X 60 ∴ ，这种情况不能围成矩形。

∴此时只能围成长30m和宽为15m的菜园面积最大，最大面积为450 的矩形，

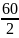推而广之，当a 60时，只能围成以墙的一部分为边围成的矩形面积最大，是长为 m，宽为 m, 最大面积为450 的矩形。

综上所述：当0＜a＜20时，以墙为边长的一部分围成的矩形面积最大，是边上为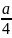（ + ）m, 最大面积为（ 的正方形; 当20≤a≤30时，两种情况面积一样大，即长为a m，宽为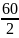（ - ）m, 最大面积为（ 的矩形; 当a 30时，只能围成以墙的一部分为边围成的矩形面积最大，即长为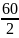 m，宽为 m, 最大面积为450 的矩形。

由此可见，四面下围时，面积最大时为正方形，而三面下围时，面积最大是并非是正方形，而是矩形；同等材料，墙体大于材料一半长度时，面积达到最大极限值。