华南师范大学 510631
摘要:图 是一个简单连通图,
是一个简单连通图, ,如果
,如果 中任意两个顶点在
中任意两个顶点在 中均不邻接,则称
中均不邻接,则称 是一个独立集(independent set);记
是一个独立集(independent set);记 为图
为图 中
中 独立集的数目,
独立集的数目, 为图G的独立数(independent number),即最大独立集中顶点的数目,于是有
为图G的独立数(independent number),即最大独立集中顶点的数目,于是有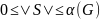 。
。
Gutman和Harary将 的发生函数
的发生函数

定义为图 的独立多项式(independent polynomial)。
的独立多项式(independent polynomial)。
Prodinger和Tichy将独立多项式的系数 求和
求和

定义为图 的Merrifield-Simmons指数或
的Merrifield-Simmons指数或 指数
指数
本文给出了一些有关图 独立多项式的计算结果、Merrifield-Simmons指数的精确计算公式以及一些恒等组合式。
独立多项式的计算结果、Merrifield-Simmons指数的精确计算公式以及一些恒等组合式。
关键词:独立多项式 Merrifield-Simmons指数
图的结构问题是图论研究中的活跃课题,包括存在性问题,算法和计数等方面。而图的独立集的研究是图论中最原始的问题之一。图论中研究的很多经典问题,如图的着色(coloring)问题、匹配(matching)问题等都和独立集密不可分,在计算机科学理论、编码学和网络理论等方面都会涉及到图的独立集问题。正因为图的独立集的研究既有重要的理论意义,也有广泛的实际应用,因此独立集的研究一直是人们的研究焦点。
为进一步考虑图的不同基数的独立集数目以及分布,Gutman和Harary引入了图的独立多项式;独立多项式亦称为Fibonacci多项式,它不仅与图论和组合数学中一些有趣的理论问题有关,而且还可以用于统计物理和理论化学的研究。自20世纪80年代初提出,它就引起很多学者的关注;一些学者研究了单圈图的独立多项式以及给出了图 的
的 独立集满足的递归公式。
独立集满足的递归公式。
由于从一个特定图多项式的系数可以得到关于图的结构组合信息的许多方面,对于独立多项式的系数Merrifield-Simmons指数,即 独立集个数之和,在1982年被Prodinger和Tichy首次提出,Merrifield和Simmons在1989年首先研究了这个指数,它是一个重要的拓扑指数,和“沸点”、“溶解度”等有机物的物理化学性质有着密切联系,一些主要研究内容是研究特殊图类的Merrifield-Simmons指数,用Merrifield-Simmons指数对树进行排序以及刻画极图;并且受Gutman复合图结果启发,一些学者利用独立多项式,得到一些有趣的组合恒等式,并给出了一些特殊类图精确的Merrifield-Simmons指数。
独立集个数之和,在1982年被Prodinger和Tichy首次提出,Merrifield和Simmons在1989年首先研究了这个指数,它是一个重要的拓扑指数,和“沸点”、“溶解度”等有机物的物理化学性质有着密切联系,一些主要研究内容是研究特殊图类的Merrifield-Simmons指数,用Merrifield-Simmons指数对树进行排序以及刻画极图;并且受Gutman复合图结果启发,一些学者利用独立多项式,得到一些有趣的组合恒等式,并给出了一些特殊类图精确的Merrifield-Simmons指数。
复杂网络中的很多统计特征具有重要的现实应用价值,而图多项式是研究图的统计特性和结构特点的重要工具,图多项式的许多性质的研究都是基于一元独立多项式开展的,独立多项式就是图中 的发生函数,利用它来研究复杂网络的统计和结构特征,成为网络科学研究的有力方法和工具指日可待。
的发生函数,利用它来研究复杂网络的统计和结构特征,成为网络科学研究的有力方法和工具指日可待。
(1) :
: 个顶点的空图。
个顶点的空图。
(2) (path):
(path): 个顶点的道路。
个顶点的道路。
(3)树(tree) :
: 个顶点,不含圈的连通图,即边数等于顶点数减1的连通图。
个顶点,不含圈的连通图,即边数等于顶点数减1的连通图。
(4) 阶完全图(complete graph)
阶完全图(complete graph) :每一对不同顶点均有一条边相邻的简单图,即
:每一对不同顶点均有一条边相邻的简单图,即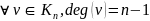 ,
, 亦称为团。
亦称为团。
(5)圈(cycle) :
: 个顶点的圈,圈的长度为
个顶点的圈,圈的长度为 。
。
(6)单圈图(unicyclic graph):只含一个圈的连通图,即边数等于顶点数的连通图。
(7)星图(star) :
: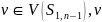 与其他
与其他 个顶点相连,之外,图中没有其它边。
个顶点相连,之外,图中没有其它边。
(8)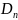 :图中顶点集为
:图中顶点集为 ,边集
,边集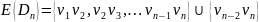 ,是树的一个特例,图2.1便是
,是树的一个特例,图2.1便是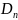 的结构。
的结构。

图2.1
(9) 蜘蛛图(spider graph):满足度至少为3的顶点至多有一个的图。
(10) 蜈蚣图 (centipede graph):
(centipede graph): ,
, 是图
是图 顶点集,
顶点集,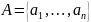 ,
, ,图
,图 的边集
的边集 , 图2.2便是
, 图2.2便是 的结构。
的结构。
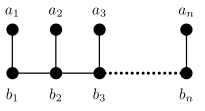
图2.2
(11) 毛毛虫图 (caterpillar graph):
(caterpillar graph): ,其中顶点集
,其中顶点集 ,这里
,这里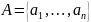 ,
, ,边集
,边集 ,图2.3便是
,图2.3便是 的结构。
的结构。

图2.3
(12)  的邻集
的邻集 :
: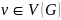 ,图
,图 中与
中与 邻接的所有顶点的集合,
邻接的所有顶点的集合, 。
。
(13)  :删除图
:删除图 中顶点
中顶点 以及与点
以及与点 所关联的边所得到的图。
所关联的边所得到的图。
(14)  :删除图
:删除图 中边
中边 所得到的图。
所得到的图。
(15) 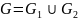 :其中
:其中 的顶点是
的顶点是 和
和 的不相交并,边集也是
的不相交并,边集也是 和
和 的不相交并。
的不相交并。
由图的独立多项式可以知道图的结构,本文介绍一些命题和定理,并由此得到一些简单图的独立多项式
命题3.1 若图 是一个
是一个 图,则
图,则 ,
,
证明 因为图 的每一个顶点都构成独立集,则
的每一个顶点都构成独立集,则 显然;
显然;
任取图 中两个点,则有
中两个点,则有 种取法,不相邻的顶点有
种取法,不相邻的顶点有
 对,则图
对,则图 中边数
中边数 为图中相邻的顶点对数,即
为图中相邻的顶点对数,即
 注:通过独立多项式可以求出图
注:通过独立多项式可以求出图 的顶点数
的顶点数 和边数
和边数
例:给定图 (如右图)
(如右图)
经计算可得:
 .事实上,
.事实上, 独立集有:
独立集有:

 图3.1
图3.1
同理可算得 .
.
于是
命题3.2 空图 ,
, .
.
命题3.3  阶完全图
阶完全图 :
: ,
,
命题3.4 圈 (
( ):
): .
.
特别地,
命题3.5 星图 :
: ,
, .
.
事实上, ,当
,当 时,
时, -独立集中所有顶点均来自
-独立集中所有顶点均来自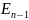 ,由命题
,由命题 知
知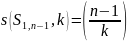 ,又
,又 ,故星图
,故星图 独立多项式即可得出。
独立多项式即可得出。
命题3.6 
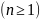 :
: ,
, .
.
事实上,Arocha证得 ,
, (
(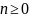 )称为斐波那契多项式,其定义为
)称为斐波那契多项式,其定义为 ,通过递推可推导出
,通过递推可推导出 的独立多项式。
的独立多项式。
下面给出两个基本定理,用于推出一些特殊简单图独立多项式的递推公式。
定理3.7 设 均是简单图,
均是简单图,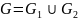 ,则
,则
证明 ∵ ,则
,则



特别地,若 ,则
,则 .
.
定理3.8 设 均是简单连通图,
均是简单连通图,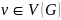 ,则
,则
证明 ∵ ,则
,则

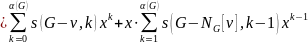

引理3.9 设 为整数,则
为整数,则

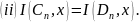
证明  时,可计算证得成立;
时,可计算证得成立;
当 时,根据定理
时,根据定理 ,得
,得


可知 ,即
,即 成立.
成立.
又∵
于是


 ,
,
则 成立。
成立。
上述引理给出圈 所满足的递推公式,并且由
所满足的递推公式,并且由 给出又一简单图
给出又一简单图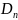 的独立多项式。
的独立多项式。
推论3.10 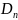 (
( ):
):
推论3.11 设 为整数,蜈蚣树
为整数,蜈蚣树 独立多项式满足的递推关系:
独立多项式满足的递推关系:


证明 当 时,经计算可得,
时,经计算可得,

当 时,由图
时,由图 得
得 ,
,
其中 是顶点数为
是顶点数为 的空图,
的空图,
因此根据定理 和定理
和定理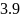 知,
知,


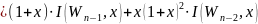

故定理得证。
同理,可得如下推论 。
。
推论3.12 设 为整数,毛毛虫
为整数,毛毛虫 独立多项式满足的递推关系为
独立多项式满足的递推关系为

 .
.
 的一些已知结果
的一些已知结果 美国化学家Richard E.Merrifield和Howard E.Simmons提出了一套根据分子结构图的有限集合上的一种拓扑指数来描述分子结构的理论,简称 指数
指数

则根据 指数定义以及命题
指数定义以及命题 至命题
至命题 很快得下面命题。
很快得下面命题。
命题4.1 星图 :
:
命题4.2 路 :
: ,
, 为第
为第 个斐波那契数。
个斐波那契数。
命题4.3 完全图 :
:
命题4.4 空图 :
:
定理4.5 简单图的 指数的计算公式
指数的计算公式
 如果
如果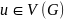 ,则
,则

 如果
如果 ,则
,则

 如果
如果 是
是 的
的 个分支,则
个分支,则

本论文主要研究了图多项式中一类:独立多项式,给出了一些简单图的独立多项式和 指数的精确形式。然而,对于给定的图
指数的精确形式。然而,对于给定的图 ,目前还没有计算独立多项式和
,目前还没有计算独立多项式和 指数的有效算法。
指数的有效算法。
参考文献:
[1]J.L.Arocha, Propriedades del polinomio independiente grafo, Revista Ciencias Matematics 137(1995) 7-18
[2]G.H.Hardy,J.E.Littlewood,G.Polya,Inequalities[M].England,Cambridge:Cambridge University Press, 1953,59:p.411-412
[3] 刘琳. 图的独立多项式研究[D].华中师范大学,2016
[4]廖云华. 图多项式若干问题研究[D].湖南师范大学,2015
[5]吴继春. 树的Merrifield-Simmons指数与独立多项式[D].湖南师范大学,2008
[6]王清秀. 图的独立多项式的一些性质研究[D].江苏师范大学,2018
[7]张海良. 关于图的两类多项式及相关指数的研究[D].华东师范大学,2013
1 / 4