湖南航天 7801研究所 湖南 长沙 410000
摘要:为满足导弹轻量化要求,弹上部件多用薄壁件。当导弹做大机动行为时,弹上薄壁部件外部压力急剧变化,部件内压力变化速率小于外部压力变化速率,内外压差使外壁受力变形。为解决这一问题,本文尝试用解析法计算弹上薄壁部件内外压差,得出薄壁部件内压力变化速率的影响因素有部件内温度、小孔孔径、小孔数量、部件外压力变化规律。建议在满足总体其他要求条件下,适当增大小孔孔径和数量。
关键字:薄壁 应变 解析
背景:
弹上部件为适应产品轻量化要求,常将产品外壳设计为薄壁,且结构紧凑[1]。当导弹做快速俯冲、爬升等大机动行为时,弹上薄壁部件外部压力急剧变化,部件内压力变化速率小于外部压力变化速率,内外压差使外壳受力变形,与其他元器件产生干涉,影响产品正常工作,甚至导致导弹发射失败[2]。
为减小薄壁部件的外壳变形程度,常在外壳上开多个小孔(下文称之为平衡孔),以减小内外压差[3]。同时为满足电磁兼容要求,孔径不能过大,开孔数量不能过多[4]。现有应变计算方法主要有两种,一是试验法,即通过地面试验模拟飞行环境,对不同孔径和小孔数量的多个产品测试,得到形变情况;二是基于流固耦合的瞬态数值仿真。
试验法受限于试验条件(设备有无、精度高低),往往成本较高,且通常很难复现实际飞行条件而出现误差[5]。基于流固耦合的瞬态数值仿真计算量极大,单个算例所需时间往往数天,甚至数周,且流体项对网格质量、计算格式和精度较为敏感,与实际结果相比误差较大[6]。
为解决这一问题,本文尝试用解析法计算弹上薄壁部件内外压差。
计算状态
已知某导弹做快速俯冲,然后巡航飞行,其中弹上薄壁部件外部压力在0~1s时,压力从0.054Mpa变化到0.189Mpa,之后压力基本保持恒定。部件内初始压力为0.054Mpa,体积5.4e-3m3。部件上开有n个孔径为r的小孔。
解析推导
本问题为瞬态绝热流动,薄壁部件小孔内外的能量方程为
 (1)
(1)
 (2)
(2)
因为部件为薄壁,且部件外空气速度为0,则有
 (3)
(3)
将气体状态方程 代入(3)求得空气质量流率
代入(3)求得空气质量流率
 (4)
(4)
薄壁部件内空气状态方程为
 (5)
(5)
对(5)求导,有
 (6)
(6)
结合公式(4)和(6)有
 (7)
(7)
又因为 ,联合上述公式,得
,联合上述公式,得

计算结果及分析
设有8个小孔,孔径为1mm,薄壁部件外压力呈线性变化。不同薄壁部件内温度,压力随时间变化如下:


图1 部件外压力变化曲线


图2 部件内压力变化曲线
图3 部件内外压力差变化曲线
设部件内温度为300K,孔径为1mm,部件外压力呈线性变化。不同小孔数量,压力随时间变化如下:

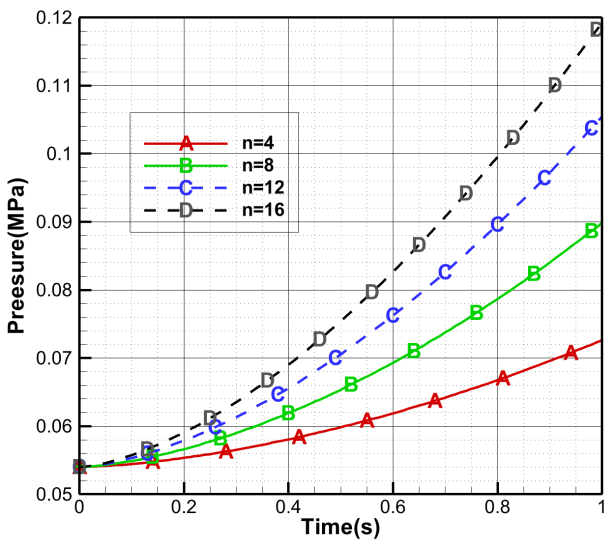
图4 部件内压力变化曲线
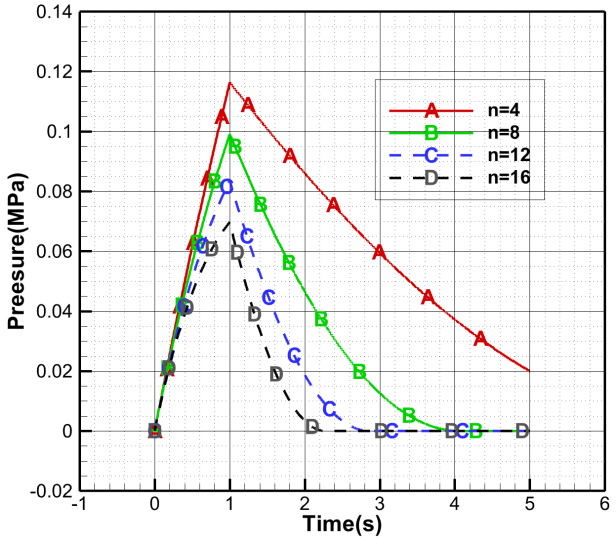

图5 部件内外压力差变化曲线
设小孔数量为8,部件内温度为300K,部件外压力呈线性变化。不同孔径,压力随时间变化如下


图6 部件内压力变化曲线


图7 部件内外压力差变化曲线
设小孔数量为8,部件内温度为300K,孔径1mm。部件外压力变化规律不同时,压力随时间变化如下

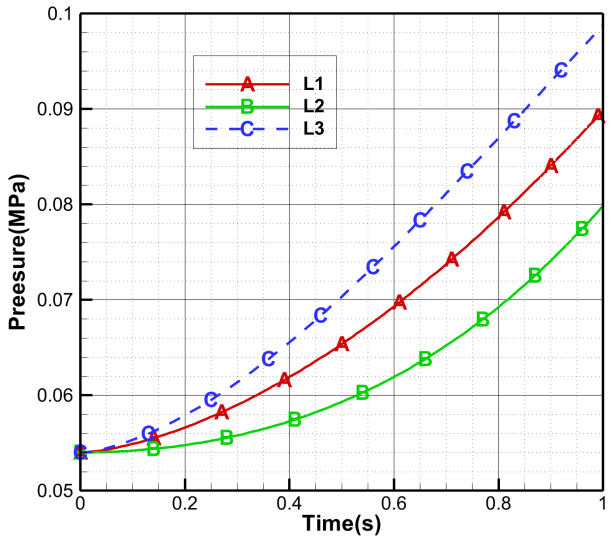
图8 部件外压力变化曲线 图9 部件内压力变化曲线

图10 部件内外压力差变化曲线
结论
本文通过解析推导,计算了不同状态下弹上薄壁部件内外压力,得到如下结论:
薄壁部件内压力变化速率的影响因素有部件内温度、小孔孔径、小孔数量、部件外压力变化规律;
薄壁部件内压力变化速率对小孔孔径、小孔数量的变化较为敏感;
建议在满足总体其他要求条件下,适当增大小孔孔径和数量。
参考文献
[1]王耀琦,梁增友,时文超,陈智刚,赵文杰. 高过载环境下薄壁金属管缓冲吸能研究[J]. 弹箭与制导学报,2018,(6).
[2]尹甲人,姚达斌. 镁合金在空空导弹导引头上应用可行性研究[J]. 航空科学技术,2014,(10).
[3]王荇卫,诸德超,吴建华,韩普祥,李祖钊. 冲击波作用下薄壁结构机弹相容性研究[J]. 振动工程学报,2004,(2).
[4]Shiping WU, Bangsheng LI, Jingjie GUO, Chengjun ZHANG, Jun JIA, Hengzhi FU. Numerical simulation for mold-filling of thin-walled aluminum alloy castings in traveling magnetic field[J]. China Foundry,2004,(2).
[5]穆建春,张铁光. 薄壁金属圆管在钝圆锥头弹体正冲击及斜冲击下破裂的实验研究[J]. 固体力学学报,2000,(1).
[6]王兴发. 火箭、飞行器材料和薄壁压力容器的渗漏判据[J]. 应用数学和力学,1986,(9).