提升钢丝绳轴向力学性能的数值求解方法

提升钢丝绳轴向力学性能的数值求解方法

任峤燚

重庆交通大学 交通运输学院 重庆市 400074

摘要：提升钢丝绳广泛运用于工业生产中，在实际工作环境中钢丝绳受力情况复杂，对设备安全性能有着显著影响。本文基于钢丝绳空间螺旋结构，建立钢丝绳理论模型，编写Fortran程序对钢丝绳力学性能进行数值求解，讨论分析钢丝绳轴向载荷对钢丝绳轴向力学性能的影响。

关键词：理论模型；数值求解；力学性能

1 提升钢丝绳理论模型

17钢丝绳是由1根芯丝加上6根侧丝捻制而成的挠性绳索[1]，基于钢丝绳复杂螺旋结构，考虑拉伸过程中的丝间接触和材料的横向变形，建立17提升钢丝绳理论模型。

（1）几何模型

本文假设在轴向拉伸载荷作用下，钢丝绳变形处于载荷应变曲线中对应的弹性阶段，同时考虑拉伸载荷施加下芯丝与侧丝的接触，以及材料的横向变形。钢丝绳芯丝与侧丝的轴向拉伸应变可表示为：

(1)

(2)

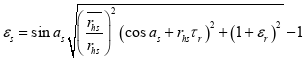(3)

式中，表示为钢丝绳绳股轴向拉伸应变，和表示为拉伸前后钢丝绳绳股长度，表示为钢丝绳芯丝轴向拉伸应变，表示为钢丝绳侧丝轴向拉伸应变，和表示为变形前后侧丝螺旋半径，表示为侧丝螺旋角，为钢丝绳扭转应变。

（2）平衡受力方程

对钢丝绳侧丝进行受力分析，基于曲杆理论，取钢丝绳侧丝上某微弧长段作为研究对象，拉伸过程中，忽略芯丝与侧丝之间的摩擦力[2]，侧丝轴线上各段的曲率、挠率并不随拉伸载荷的变化而变化。钢丝绳侧丝的受力平衡方程可表示为：

(4)

(5)

(6)

式中，为侧丝截面处所受的沿副法向方向上的剪切力，为侧丝变形后的挠率，为侧丝轴向拉力，为变形后侧丝上副法向的曲率，为单位长度侧丝轴线所受的沿侧丝主法向的线载荷，为为侧丝截面处关于主法向方向的弯矩，为侧丝截面扭矩，为侧丝的弹性模量，为变形后的侧丝横截面积。

（3）丝间接触模型

考虑拉伸过程中芯丝与侧丝的接触，将接触区域沿较长方向的区域中线定义为接触线，取接触线上一点为研究对象，该点处的接触模型可表示为：

(7)

(8)

式中，为该点处的接触间隙，为接触变形前的初始间隙，为芯丝在该点处沿副法向方向的弹性变形，为侧丝在该点处沿副法向方向的弹性变形，为芯丝和侧丝在该点处沿副法向方向的相对刚体位移，为单位长度接触线所受的接触力，为该点处的接触压力。

2 数值求解流程

本文基于Fortran编程语言，采用半解析法对提升钢丝绳轴向力学性能进行求解，相比于传统试验与有限元方法求解速度更快。在离散接触区域时，求解精度与求解效率受到计算域网格疏密的影响，当计算域网格越密时，求解精度越高，求解效率越低。当计算域网格越疏时，求解精度越低，求解效率越高。网格疏密的划分需要协调求解精度与求解效率。

本文先根据假设的总接触变形量对芯丝和侧丝各自的接触变形量进行计算，将芯丝与侧丝的接触变形量作为参数输入钢丝绳几何模型和平衡受力方程，得到钢丝绳轴向力学性能，包括钢丝绳轴向力，钢丝绳芯丝与侧丝轴向拉伸应变。为修正总接触变形量，得到精确结果，需要将平衡受力方程的结果作为参数输入钢丝绳接触模型，得到钢丝绳总接触变形量。通过将其与假设的总接触变形量进行迭代误差分析修正总接触变形量。

3 结果与讨论

在拉伸载荷的作用下，考虑钢丝绳材料特性和结构特点，本文所研究的17钢丝绳几何参数与材料参数设置为钢丝绳芯丝直径3.94mm，钢丝绳侧丝直径3.73mm，钢丝绳捻角为。钢丝绳芯丝与侧丝为同一种材料，弹性模量为197.9GPa，泊松比为0.3。

图1给出了不同轴向拉伸载荷下的钢丝绳股轴向力的变化，由图可知，随着轴向拉伸载荷增加，钢丝绳股轴向拉力呈线性增加。在弹性阶段范围内，钢丝绳股轴向力增加与轴向拉伸载荷有关，所以在工程中，钢丝绳不得超负荷使用，避免在冲击载荷下工作，速度应平稳。

图1 不同轴向拉伸载荷下的钢丝绳轴向力

图2给出了不同轴向拉伸载荷下的钢丝绳芯丝和侧丝的轴向拉伸应变，由图可知，随着轴向拉伸载荷的增加，钢丝绳芯丝和侧丝的轴向拉伸应变呈线性增加，钢丝绳芯丝轴向拉伸应变与钢丝绳绳股轴向拉伸应变相等，随着拉伸载荷的增加，钢丝绳侧丝轴向拉伸应变增加速度减缓，表明在拉伸过程中，随着轴向拉伸载荷的增加，钢丝绳芯丝所受的拉伸载荷会大于侧丝轴向拉伸载荷，更容易失效。

图2 不同轴向拉伸载荷下的钢丝绳轴向应变

总结

本文对拉伸工况下钢丝绳轴向力学性能进行了研究，基于钢丝绳复杂螺旋结构，考虑钢丝绳材料特性，建立了钢丝绳理论模型。分析得到了不同轴向拉伸载荷下的钢丝绳轴向力学性能，所得结论如下：

（1）弹性阶段内，随着拉伸载荷增大，钢丝绳轴向力呈线性增加，在弹性阶段范围内，钢丝绳股轴向力增加与轴向拉伸载荷有关。

（2）随着轴向拉伸载荷的增加，钢丝绳芯丝和侧丝的轴向拉伸应变呈线性增加，钢丝绳侧丝轴向拉伸应变增加速度小于芯丝，钢丝绳芯丝所受的拉伸载荷会大于侧丝轴向拉伸载荷。

参考文献：

[1] 张瑾, 陈向阳, 唐文亭, 刘力红. 1×7+IWS结构钢丝绳有限元分析[J]. 安徽理工大学学报(自然科学版), 2014,34(03):83-86.

[2] Argatov I. Response of a wire rope strand to axial and torsional loads: Asymptotic modeling of the effect of interwire contact deformations[J]. International Journal of Solids and Structures, 2011,48(10):1413-1423.