1.中电信量子信息科技集团;
2.科大国盾量子技术股份有限公司;
3.中电信量子信息科技集团有限公司;
4.科大国盾量子技术股份有限公司;
5.中电信量子科技有限公司
摘要:为了降低量子通信部署的成本,一种可行的方案是将其与现有的通信网络进行融合,将QKD(quantum key distribution,量子密钥分发)系统与DWDM(Dense wavelength pision multiplexer, 密集波分复用)系统进行波分复用,利用现有光纤网络进行共纤传输。本文考虑光纤扰动等因素,提出了一种在波分复用情境下QKD成码率的有效计算方式,并通过实验验证了该方法的有效性。并在30,40,50 km长的光纤中,测试了QKD成码率为1 kbps的条件下,DWDM系统总光功率对应值,验证了经典光-量子光波分复用系统的可行性。
关键词:量子通信;波分复用;蒙特卡罗
中图分类号:TP393 文献标识码:A
doi: 10.11959/j.issn.1000-0801.2016xxx
Study on the co-propagating of QKD and DWDM signals
WangZhen MaRui WangLei TangShibiao PengXingXiang
Abstract:To reduce the cost of quantum communication deployment, a feasible solution is to integrate it with the existing communication network.We canmultiplex the quantum QKD system and DWDM system with wavelength pision multiplexing technology, and use the existing optical fiber network forco-propagating. In this paper,considering factors such as optical fiber perturbation, an effective calculation method for QKD’s bitrate in the scenario of wavelength pision multiplexing is proposed, and the effectiveness of the method is verified by experiments. The corresponding total optical power values of the DWDM system were tested under the condition that QKD’sbit rates are 1 kbps in optical fibers with lengths of 30, 40, and 50km, and the feasibility of the classical-quantum optical wavelength pision multiplexing system is verified.
Key words: quantum communication, wavelength pision multiplexing, monte carlo
1 引言
传统通信密码体系中加密方式主要分为对称密钥加密算法和非对称密钥加密算法,其中非对称密钥加密算法常用作对称密钥的密钥分发。非对称密钥算法的安全性由数学问题的复杂性来保障,如基于大数质因子分解的RSA、基于离散对数的ElGamal和基于椭圆曲线的ECC等算法。而随着算力的提升以及新兴技术的出现,现行算法的安全性正受到严重威胁,比如1994年Shor提出Shor算法[1],该算法可用于计算大整数的质因数分解,时间复杂度为多项式阶。为了应对该问题,目前比较流行的一种解决方式是QKD技术,其安全性由不可测量和不可克隆等物理性质保证,因此从原则上讲是不可攻破的。
1984年,Bennett等人提出了世界上首个QKD协议——BB84协议[2]。随后该领域逐渐成为研究热点,1991年Ekert等人提出E91协议[3],该协议使用纠缠光子来实现密钥分发;1992年,Bennett等人提出基于纠缠的协议BBM92[4],并证明了其与BB84协议的等价性。目前基于光纤传输的QKD系统传输最远距离超过800 km[5],基于卫星的QKD系统最远传输距离已超过1 200 km[6]。QKD技术的日益成熟也将实用化推上进程,但在实际建设过程中铺设光纤成本较高,需要研究设计可行的量子光-经典光共纤方案。
早在1997年,Townsend小组就进行了第一个QKD与经典光通信的共纤演示实验[7]。随后更多研究人员将研究方向转移到共纤传输领域,在实验室环境和外场环境中对波分复用系统展开研究[8-10]。但目前这些研究广泛集中于将量子光分配到C波段以降低光纤损耗影响,比如2018年钱懿等人研究了单纤双向和双纤双向共纤传输方案[11],量子光波长为1 550.12 nm,经典光波长分别为1 590 nm、1 610 nm、1 310 nm和1 551.72 nm和1 552.52 nm。但在实际光通信网络中,经典光通信已广泛使用C波段作为传输波长,量子光波长采用C波段会导致经典光通信的拉曼散射噪声较大,进一步影响QKD成码。还需解决量子光和经典光异波段传输的问题,主流思路是将QKD工作波长设为O波段。1997年Townsend等人的工作便是将量子光信号波长设为1 310 nm,与1 550 nm的1.2 Gbps经典光在28 km的光纤上复用[7];2018年Y. Mao等人实现了QKD设备和21 dBm的3.6 Tbps商用骨干网设备在66 km光纤上的复用[12],量子光波长为1 310 nm,经典光波长为1 528~1 538 nm的20个波道;2021年Jia-Qi Geng等人实现了QKD设备和80 Gbps经典光信号在超过50 km光纤上的复用[13],经典光信号功率为15 dBm,量子光波长为1 310 nm,经典光波长为1 544~1 548 nm,对应波道为C28-C56。
目前主要研究尚缺乏对80波经典光通信系统与QKD设备复用的可行性研究和实验演示,2018年唐建军等人虽然对80波DWDM系统与QKD系统的波分复用可行性作了部分研究[14],但其为了降低经典光对QKD系统的影响,将经典光光功率衰减至1.5 dBm,在实际应用场景下该做法会导致经典通信的业务能力下降。并且在经典光-量子光共纤传输系统中的QKD设备由于其不稳定性往往导致理论计算所得的成码率与实际成码率具有较大差距,目前业界尚缺乏有效的计算工具,本文利用蒙特卡罗模拟法对QKD设备的成码率进行了模拟计算,与实际数据拟合效果较好。本文还对80波DWDM系统和QKD设备的复用进行了进一步可行性验证,发现在30 km,40 km和50 km的光纤中复用传输时,80波DWDM经典光功率超过10 dBm仍可保证QKD成码率大于1 kbps。
2经典光与量子光共纤传输系统噪声分析
2.1 噪声来源
共纤传输系统由经典光系统和QKD系统两部分组成。由于现有的经典光传输网络普遍使用C波段作为传输光波长,为防止经典光信号对量子光信号的噪声难以消除,本文的QKD系统量子光信号波长采用1 310 nm。量子光信号往往处于单光子水平,约为-70~-85 dBm,对经典光系统影响较小。而经典光系统引入的噪声对QKD系统的成码率影响较大,BB84协议成码率公式为:
![]() (1)
(1)
这里q为基矢筛选效率,平衡选基方案下为0.5;![]() 为QKD发送端信号态的平均光子数;
为QKD发送端信号态的平均光子数;![]() 为QKD接收端对真空态的响应率,由SPD暗计数及信道噪声引起;
为QKD接收端对真空态的响应率,由SPD暗计数及信道噪声引起;![]() 为QKD接收端对单光子态的响应率;
为QKD接收端对单光子态的响应率;![]() (x)为二值香农熵函数;
(x)为二值香农熵函数;![]() 为QKD系统单光子态的错误率;
为QKD系统单光子态的错误率;![]() 为QKD接收端对信号态脉冲的探测率;
为QKD接收端对信号态脉冲的探测率;![]() 为纠错处理过程的纠错效率,定义为纠错过程交互公开信息量与香浓极限的比率;
为纠错处理过程的纠错效率,定义为纠错过程交互公开信息量与香浓极限的比率;![]() 为信号态的误码率。
为信号态的误码率。
根据公式容易看出探测器对单光子态的响应率降低和误码率上升会导致成码率降低,分别对应于光学系统的传输损耗和噪声。传输损耗可分为光纤衰减和光纤耦合衰减,光纤衰减包括吸收损耗和散射损耗等,光纤耦合衰减指光纤法兰适配器连接损耗和熔接损耗。有文献指出噪声主要包含以下三个方面[15]:
1)色散,多模光纤存在模间色散,单模光纤存在偏振色散和色度色散等情况,往往色度色散占据主要效应。色散会导致量子光脉冲展宽,单光子落在探测器有效门宽外从而降低响应率,或者落在相邻探测器门宽内导致错误率升高。光通信网络中常用的光纤为G.657,零色散点在1 310 nm处,色散系数小于0.092 ps/nm/km,通常QKD量子光信号谱宽控制小于0.1 nm。这意味着当量子光选用1 310 nm,传输30~60 km导致的脉冲展宽小于0.1 ps,远小于探测器门宽(~100 ps),因此色散导致的噪声效应和衰减效应可忽略。
2)散射效应,散射效应分为两种,分为弹性散射的瑞利散射和非弹性散射的布里渊散射和拉曼散射。其中瑞利散射不会产生新的频谱成分,因此可通过频域滤波滤除此部分噪声。而布里渊散射引入的频移约10 GHz[15],远小于O波段与C波段间隔,引入噪声可以忽略不计。拉曼散射引入的峰值斯托克斯频移为13 THz,增益谱约40 THz,对应320 nm,是主要噪声源。2009年,Peters等人给出经典光-量子光共纤系统中的同向拉曼散射噪声公式如下
[16]:
 (2)
(2)
这里![]() 是经典光的入射光强,
是经典光的入射光强,![]() 是经典光的自发拉曼散射系数,
是经典光的自发拉曼散射系数,![]() 和
和![]() 分别是经典光和量子光在光纤中的衰减系数,
分别是经典光和量子光在光纤中的衰减系数,![]() 表示在光纤长度z处的拉曼噪声。
表示在光纤长度z处的拉曼噪声。
则经典光在量子信道产生的拉曼噪声功率为:
![]() (3)
(3)
这里的![]() 为带通滤波片带宽,
为带通滤波片带宽,![]() 为QKD接收端单光子探测器单个门门宽,
为QKD接收端单光子探测器单个门门宽,![]() 为单光子探测器门重复频率。
为单光子探测器门重复频率。
3)四波混频,即不同波长的三个光子相互作用在新波长处产生光子的效应,假定三个光子频率分别为![]() ,
,![]() ,功率分别为
,功率分别为![]() ,
,![]() 。产生光子频率为[16]:
。产生光子频率为[16]:
![]() (4)
(4)
功率为:
![]() (5)
(5)
这里![]() 是光纤衰减系数,
是光纤衰减系数,![]() 是四波混频效率,
是四波混频效率,![]() 是光纤的三阶非线性系数,
是光纤的三阶非线性系数,![]() 是四波混频简并因子。如果三个光子的波长都相同则
是四波混频简并因子。如果三个光子的波长都相同则![]() ,如果两个光子波长相同则
,如果两个光子波长相同则![]() 。四波混频效率可按照如下公式计算:
。四波混频效率可按照如下公式计算:
![]() (6)
(6)
此处的![]() 为相位匹配因子:
为相位匹配因子:
![]() (7)
(7)
![]() 是不同波道的传播常数。若经典光波长在C波段,即频率为196.65-192.7 THz之间,此时产生的四波混频噪声成分波长最低的为1 494.5 nm,远离量子光波长,同样可通过频域滤波滤除此噪声,因此四波混频噪声不是影响QKD成码性能的主要因素。
是不同波道的传播常数。若经典光波长在C波段,即频率为196.65-192.7 THz之间,此时产生的四波混频噪声成分波长最低的为1 494.5 nm,远离量子光波长,同样可通过频域滤波滤除此噪声,因此四波混频噪声不是影响QKD成码性能的主要因素。
除此以外,如果分/合波器件隔离度较差,还会引入经典光的串扰噪声;以及若经典光频谱较宽,会引入频谱泄露噪声。但这两部分噪声可通过级联带通滤波片滤除,因此可忽略其影响。
2.2 理论计算和实验数据
综上所述,在QKD-经典光共纤传输系统中,量子光对经典光信号的影响较少,经典光信号对量子光信号的影响主要体现在拉曼噪声,这也是共纤传输系统中限制QKD成码率的主要瓶颈因素之一。由于同向拉曼噪声往往小于背向拉曼噪声[14],为了减少其影响,本文的共纤传输系统采用量子光和经典光同步传输的方案设计。
为对共纤传输系统中QKD系统的成码性能进行建模,先分析和测试拉曼噪声,由于经典光信号引起的拉曼噪声同样是单光子量级,因此需用单光子探测器进行测量。具体光路搭建如图1所示,红色箭头代表C波段光传播路径,黑色箭头为1 310 nm光传播路径。经典光收发器用于产生C波段的经典光信号,波分复用模块1、光纤盘和波分复用模块2用于模拟经典光在共纤传输系统中的传播过程,可调VOA用于模拟补偿实际光纤系统中的光纤跳变点所带来的光传播损耗,带通滤波模块和单光子探测器置于末端用于探测拉曼噪声计数。

图1 拉曼散射噪声测试光路示意图
可以计算得到测量的拉曼噪声光子数为:
![]() (8)
(8)
这里![]() 为单光子探测器的探测效率;
为单光子探测器的探测效率;![]() 为除去光纤损耗外的其余损耗;
为除去光纤损耗外的其余损耗;![]() 为拉曼噪声的波长,由于会用带通滤波片对拉曼噪声的波长进行滤波,因此
为拉曼噪声的波长,由于会用带通滤波片对拉曼噪声的波长进行滤波,因此![]() =1 310 nm。主要参数如表1所示:
=1 310 nm。主要参数如表1所示:
表1 拉曼噪声计算主要参数
参数 | 数值 |
| 0.2 |
| 1.2 dB |
| 0.2 nm |
| 125 ps |
| 1.25 GHz |
当固定光纤长度为50 km时,拉曼散射噪声与入射端经典光功率的关系理论值与实验值如图1(a)所示;当固定经典光入射端光功率为10 dbm时,通过更换不同长度的光纤盘可测得拉曼散射噪声与光纤长度的关系如图1(b)所示,黑色实线为理论计算数值,红色圆圈为实验测量值,可以发现采用上述方法的理论计算与实验结果拟合良好。且对公式(8)经过分析可以发现同向拉曼散射噪声随光纤长度的变长而降低的根源来自于项![]() ,即光纤对经典光信号的功率衰减,从而导致其产生的拉曼噪声进一步降低。但实际上若考虑量子光的信噪比,则其一定包含项
,即光纤对经典光信号的功率衰减,从而导致其产生的拉曼噪声进一步降低。但实际上若考虑量子光的信噪比,则其一定包含项![]() ,故虽然当光纤距离大于20 km时拉曼散射噪声不断降低,但信噪比实际上亦在不断降低,从而导致QKD成码率逐渐下降。因此除了经典光信号光功率外,光纤长度也是限制QKD成码率的主要因素之一。
,故虽然当光纤距离大于20 km时拉曼散射噪声不断降低,但信噪比实际上亦在不断降低,从而导致QKD成码率逐渐下降。因此除了经典光信号光功率外,光纤长度也是限制QKD成码率的主要因素之一。


(a)拉曼噪声和经典光功率关系 (b)拉曼噪声和光纤长度关系
图2 拉曼散射噪声计算
3QKD设备成码率
3.1 波分复用系统方案
本文搭建经典光-量子光波分复用系统方案如图3所示,红色箭头为经典光信道,黑色箭头为量子信道。经典光收发器为华为的80×100 Gbit/s的商用设备,可收发80波的DWDM光,信道间隔为50 GHz,并可调节经典光大小,设置使之收发波长为192.7~196.65 THz的经典光。
QKD发送端和QKD接收端共同构成QKD系统,本文采用国盾量子的MHz QKD商用设备——基于偏振编码的诱骗态BB84协议,量子光波长为1 310 nm,重复频率为125 MHz。
波分复用模块1和2对量子光和经典光分别进行合波与分波,插入损耗小于1 dB,波分复用模块2的隔离度大于30 dB。
带通滤波模块用于滤除除拉曼噪声外的其余噪声以提升QKD系统性能,隔离度大于70 dB,信道通带带宽为![]() 。
。

图3 经典光-量子光波分复用系统测试环境示意图
3.2 安全成码率公式修正
虽然(1)式给出了QKD设备的成码率计算公式,在实际的QKD设备中往往还需要考虑有限码长效应,计算成码率的最低值。
假定QKD设备重复频率为![]() ,则发送端在时间T内发送的总脉冲数为
,则发送端在时间T内发送的总脉冲数为![]() ,发送信号态、诱骗态和真空态的概率分别为
,发送信号态、诱骗态和真空态的概率分别为![]() ,则该段时间内发送的信号态、诱骗态和真空态数量依次为:
,则该段时间内发送的信号态、诱骗态和真空态数量依次为:
![]() ,
,![]() ,
,![]() (9)
(9)
信号态、诱骗态和真空态平均单脉冲光子数分别为:![]() 0。单光子探测器在时间T内的固有暗计数为
0。单光子探测器在时间T内的固有暗计数为![]() ,因此在经典光与量子光共纤传输系统中:
,因此在经典光与量子光共纤传输系统中:
![]() (10)
(10)
假定光纤长度为![]() ,则增益概率为:
,则增益概率为:
![]() (11)
(11)
![]() (12)
(12)
因此接收端接收的信号态、诱骗态和真空态数目分别为:
![]() ,
,![]() ,
,![]() (13)
(13)
根据简单的统计涨落分析可以得到[17]:
![]() (14)
(14)
这里的上标L和U分别代表统计估计的参量的下限和上限,![]() 是置信度。假定
是置信度。假定![]() 分别是信号态、诱骗态和真空态所测得的错误率,
分别是信号态、诱骗态和真空态所测得的错误率,![]() 为系统光学自带的光学错误,所有探测到的脉冲都存在此错误,当发送端发送真空态时接收端测得光子完全来源于单光子探测器的暗计数和拉曼噪声,因此其偏振可认为是杂乱无章的,错误概率
为系统光学自带的光学错误,所有探测到的脉冲都存在此错误,当发送端发送真空态时接收端测得光子完全来源于单光子探测器的暗计数和拉曼噪声,因此其偏振可认为是杂乱无章的,错误概率![]() 。同理,当QKD发送端发射信号态和诱骗态时,若QKD接收端探测光子不来自于QKD发送端,则错误概率同
。同理,当QKD发送端发射信号态和诱骗态时,若QKD接收端探测光子不来自于QKD发送端,则错误概率同![]() ;反之错误率为
;反之错误率为![]() ,因此可以得到[17]:
,因此可以得到[17]:
![]() (15)
(15)
![]() (16)
(16)
同理,可根据统计分析得到:
![]() (17)
(17)
将(14),(17)式带入如下公式[17]可计算得到![]() 和
和![]() 。
。
![]() (18)
(18)
![]() (19)
(19)
根据下式可计算得到![]() :
:
![]() (20)
(20)
将(14),(18),(19),(20)代入(1)式可得成码率为:
![]() (21)
(21)
3.3 蒙特卡罗模拟
实际上QKD运行过程中成码率并不会如3.2节一般稳定,比如随着光纤的微小抖动以及冷热变化会导致量子态偏振与预先校准好的偏振产生偏移,从而导致成码率下降;其次QKD设备一般在运行时需要消耗相当一部分时间用于启动;且在运行过程中,QKD设备会不断执行检测程序,若某一段时间内错误率高于某个阈值![]() 则中断成码,重新启动执行校准环节。无疑上述因素都会导致工程上的QKD设备成码率低于理论预期。
则中断成码,重新启动执行校准环节。无疑上述因素都会导致工程上的QKD设备成码率低于理论预期。
为了使理论计算符合预期,为后续的方案设计提供指导意见,本文还利用蒙特卡罗方法对QKD设备的实际运行过程进行研究。
假定预期量子态偏振方向与实际量子态偏振方向夹角定义为偏振调制偏差角![]() ,当QKD设备校准完毕后
,当QKD设备校准完毕后![]() ,此时由于光学器件的不完美性仍会引入
,此时由于光学器件的不完美性仍会引入![]() 的错误率。光纤系统的扰动导致
的错误率。光纤系统的扰动导致![]() 遵循一维随机布朗运动。假定间隔单位时间,
遵循一维随机布朗运动。假定间隔单位时间,![]() 时刻信号态的光学错误率更新为:
时刻信号态的光学错误率更新为:
![]() (22)
(22)
将(22)式代入(15)-(21)即可求出该单位时间内的成码率,一段时间内的总成码率即为该时间内每个单位时间成码量的和除以总时间。
除此以外,还需要考虑QKD启动时间所造成的影响,即使QKD在进入成码流程后仍会不断地检测信号态错误率,若错误率高于某一特定阈值则会中止流程,重新启动QKD设备以进行设备校准。当经典光功率较强,信噪比较低时,QKD设备会反复重新启动,此时启动所花费时间为影响QKD成码率的主要因素之一。显然,当经典光功率越强,单次启动校准所需时间会越多,假定QKD设备单次启动耗时为![]() ,可建模为:
,可建模为:
![]() (23)
(23)
这里的![]() 为经典光光功率,
为经典光光功率,![]() 用于衡量启动过程中与经典光功率无关的环节所消耗的时间,为固定时间,
用于衡量启动过程中与经典光功率无关的环节所消耗的时间,为固定时间,![]() 为常数。若希望模拟计算时间T’内经典光与量子光共纤传输系统中QKD设备的平均成码率大小,计算流程框图如图4所示。
为常数。若希望模拟计算时间T’内经典光与量子光共纤传输系统中QKD设备的平均成码率大小,计算流程框图如图4所示。
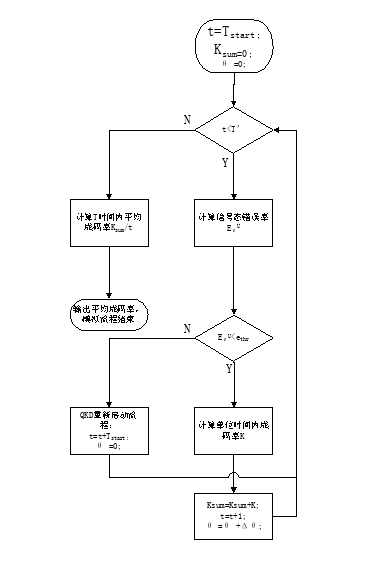
图4 蒙特卡洛模拟流程框图
关键步骤如下:
1)QKD设备初始化,进行相互验证、协商通信、偏振纠偏等过程,花费时间![]() ;
;
2)时间判决,判断当前时间t是否小于T’,若满足则跳到步骤3),否则跳到步骤6);
3)错误率判决,计算信号态错误率,并判断是否小于给定阈值,如果小于给定阈值则进入步骤4),否则进入步骤5);
4)计算单位时间内成码率,并更新累计密钥量、时间和偏振调制偏差角,并回到步骤2);
5)QKD重新进行初始化,花费时间![]() ,更新时间并初始化偏振调制偏差角,回到步骤2);
,更新时间并初始化偏振调制偏差角,回到步骤2);
6)计算持续时间T’内的平均成码率,并输出结果。
4实验结果
若固定光纤盘长度为50 km,改变经典光信号的光功率,30 min内的平均成码率测试结果如图5(a)、(b)所示;若固定经典光光信号的光功率为10 dBm,改变光纤盘长度,30 min内的平均成码率测试结果如图5(c)、(d)所示。图(a)、(c)中黑色实线为利用式(21)计算结果,图(b)、(d)中黑色实线为利用3.3节中的蒙特卡罗模拟法计算结果,蒙特卡罗模拟主要参数如表2所示,图(a)、(b)、(c)、(d)中的空心红色圆圈代表实测数据。可以发现当经典光信号的光功率增加时,成码率降低,与预期相符;当传输距离增加时,成码率会迅速降低,下降速度逐渐减小,说明在短距离成码时虽然QKD性能表现较好,但此时传输距离对成码率影响较大,长距离成码时虽然QKD成码率较低,但此时对传输距离不敏感。同时可以发现仅用(21)式计算结果与实际QKD的成码率具有较大差异,用蒙特卡罗模拟法所计算得到的成码率则与实际成码率拟合较好,验证了此方法的有效性。


(a)光纤长度为50 km,理论计算值与实测数据 (b)光纤长度为50 km,仿真模拟值与实测数据


(c)经典光功率为10 dBm,理论计算值与实测数据 (d)经典光功率为10 dBm,仿真模拟值与实测数据
图5 成码率与经典光功率和光纤长度关系
表2 蒙特卡罗模拟主要参数
参数 | 数值 |
d | 2 |
k | 0.05 |
m | 2 |
| 0.1 |
| 2.734% |
| 0.71% |
若更换带通滤波模块为信道通带带宽![]() 的滤波器件,仿真结果如图6所示,固定经典光光功率为10 dBm,黑色实线为带宽0.2 nm的滤波器件仿真结果,红色实线为带宽0.1 nm的滤波器件仿真结果。可以发现当传输距离较短时,更换不同带宽的滤波器件对成码率影响较小,当传输距离较远时,小带宽的滤波器件会对成码率有明显改善。
的滤波器件,仿真结果如图6所示,固定经典光光功率为10 dBm,黑色实线为带宽0.2 nm的滤波器件仿真结果,红色实线为带宽0.1 nm的滤波器件仿真结果。可以发现当传输距离较短时,更换不同带宽的滤波器件对成码率影响较小,当传输距离较远时,小带宽的滤波器件会对成码率有明显改善。

图5 成码率与带通滤波模块关系
为进一步滤除经典光对QKD设备的影响,将图3中的带通滤波模块替换为带宽0.1 nm的带通滤波器件,测试光纤传输距离分别为30 km,40 km和50 km时,24 h内成码率为1 kbps所对应的经典光信号的光功率,测试结果如表3所示。可以发现即使经典光功率大于10 dBm,仍可保证QKD系统长码率大于1 kbps。
表3 不同共纤光纤距离时1kbps成码率对应经典光光功率
光纤距离/km | 经典光功率/dBm |
30 | 12.84 |
40 | 12.04 |
| 11.44 |
4 结束语
采用波分复用的方式部署QKD系统可以有效降低部署成本,节省额外部署的光纤等资源。本文创造性地提出一种新的方法用以模拟计算波分复用系统中QKD设备的成码率,和实测数据拟合较好,并以该方法作为指导,对带通滤波模块参数进行优化。并在优化后的方案中测试了QKD系统的成码率性能,验证了经典光-量子光共纤传输系统的可行性,容量(8 Tbit/s,80 个波长,单波长100 Gbit/s)在业界处于领先水平,可为工程界实施经典光-量子光波分复用提供指导依据。
参考文献:(参考文献格式参照2015年新标准GBT 7714-2015)
[1]Shor, P W. Algorithms for quantum computation: discrete logarithms and factoring[J]. IEEE Comput. Soc. Press, 1994: 124–134.
[2]BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing[C]//International Conference on Computers, Systems, and Signal Processing, December 10-12, 1984, Bangalore, India. Piscata way: IEEE Press, 1984: 175-179.
[3]EKERT A. Quantum cryptography based on bell’s theorem[J]. Physical Review Letter, 1991, 67(6): 661-663.
[4]BENNETT C H, BRASSARD G, MERMIN N D. Quantum cryptography without bell’s theorem[J]. Physical Review Letters, 1992, 68(5): 557.
[5]WANG S, YIN Z Q, HE D Y, et al. Twin-field quantum key distribution over 830-km fibre [J]. Nature Photonics, 2022, 16(2): 154-161.
[6]YIN J, CAO Y, LI Y H, et al. Satellite-based entanglement distribution over 1200 kilometers [J]. Science, 2017, 356(6343): 1140-1144.
[7]TOWNSEND P D. Simultaneous quantum cryptographic key distribution and conventional data transmission over installed fibre using wavelength-pision multiplexing[J]. Electronics Letters, 1997, 33(3): 188-190.
[8]Patel K A,Dynes J F,Choi I,et a1.Coexistence ofhigh-bit-rate quantum key distribution and data on optical fiber[J].Phys.Rev.X,2012,2(4):041010.
[9]Valivarthi R, Umesh P, John C,et a1.Measurement-device-independent quantum key distribution coexisting with classical communication[J].Quantum Science and Technology, 2019, 4(4):045002.
[10]Eriksson T A,Hirano T,Puttnam B J,et a1.Wavelength pision multiplexing ofcontinuous variable quantum key distribution and 1 8.3 Tbit/s data channels[J].Communications Physics,2019,2(1):9.
[11]钱懿,林翔宇,王东,等.量子密钥分发和经典光通信波分复用共纤传输研究[J],电信科学,2018,34(9):48-62.
Qian Y, Lin X, Wang D, et al. Study of “quantum + classical” wavelength pision multiplexing technique in optical network[J]. Telecommunications Science, 2018, 34(9):48-62.
[12]Mao Y, Wang B X , Zhao C, et al. Integrating quantum key distribution with classical communications in backbone fiber network[J]. Opt. Express, 2018, 26(5):6010-6020.
[13]Geng J Q,Fan-Yuan G J,Wang S,et a1.Coexistence ofquantum key distribution and optical transport network based on standard single—mode fiber at high launch power[J].Opt.Lett., 2021,46(11):2573-2576.
[14]唐建军,李俊杰,张成良,等.开放型量子保密通信系统架构及共纤传输技术研究与实验[J],电信科学,2018,34(9):28-36.
Tang J J, Li J J, Zhang C L, et al. Research and experiment of open quantum cryptography communication system architecture and co-fiber transmission technology[J]. Telecommunications Science, 2018, 34(9):28-36.
[15]王碧霄. 量子密钥分发与经典光通信共纤传输的实验研究[D]. 合肥:中国科学技术大学, 2021.
Wang B X. Experimental study on the co-propagation of quantum key distribution and classical optical communication over the same fiber[D]. He fei: University of Science and Technology of China, 2021.
[16]Chapuran T E, Toliver P, Peters N A, et a.Optical networking for quantum key distribution and quantum communications[J].New Journal of Physics, 2009, 11(10):105001.
[17]刘洋. 远距离量子密钥分发系统的相关研究[D].合肥:中国科学技术大学, 2012.
Liu Y. The experimental study of long range Quantum key distribution system[D]. He fei: University of Science and Technology of China, 2012.
[作者简介]
1、王振(1980--),男,汉族,陕西西安,博士,中电信量子信息科技集团,副总经理,230088,主要研究方向为量子通信、量子计算
2、马睿(1987--),女,汉族,山西大同,研究生,科大国盾量子技术股份有限公司,230088,主要研究方向为单光子探测器,量子通信等
3、王雷(1985--),男,汉族,安徽利辛,研发与运营中心总经理助理/工程师,本科,中电信量子信息科技集团有限公司,230088,研究方向:软件研发、量子通信、量子计算云平台等
4、唐世彪(1982-),男,汉,广西桂林,副总裁/正高级工程师,博士,科大国盾量子技术股份有限公司,230088,主要研究方向为光量子器件,量子通信、量子计算等。
5、彭星翔(1995-),男,汉,重庆市,博士,中电信量子科技有限公司,230061,主要研究方向为量子通信、量子算法、量子密钥分发协议和经典光通信网络融合。