中国电子科技集团第36研究所,浙江嘉兴 314033
摘要:现今,无源测向技术因其自身所具备的优点被应用的越来越广泛,相关的研究文献也从各自角度提出了提高测向精度的方法,但较少考虑被测机动目标自身的运动特性。本文在相位干涉仪测向算法基础之上,结合被测机动目标运动特性建立系统模型。由于系统非线性,提出基于扩展卡尔曼滤波(EKF)针对机动目标的相位干涉仪测向算法。经仿真表明,新提出算法较常规相位干涉仪测向方式测向精度有明显改善。
关键词:相位干涉仪测向,机动目标,EKF,非线性系统
Phase Interferometer Direction Finding Algorithm based on EKF for Maneuvering Target
Xuhui Jiang, Duoyun Zhang, Qinzhi Li
The 36th Research Institute of CETC, Zhejiang Jiaxing 314033
Abstract: Nowadays, the passive direction finding is applied more and more widely because of its advantages. The methods have been proposed from their respective perspectives in the relevant articles to improve the accuracy. However, in the articles the motion characteristics of the maneuvering target are ignored. Consider the phase interferometer direction finding and the motion characteristics of maneuvering target, a system model is constructed in this paper. Because the system is non-linear, the phase interferometer direction finding algorithm based on EKF for maneuvering target is proposed. The simulation results show that the accuracy of the new algorithm is better than that of the conventional phase interferometer direction finding method.
Key word: phase interferometer direction finding, maneuvering target, EKF, non-linear system
0 引言
在通信对抗领域无源定位测向技术发展很早,相比较有源定位技术具有工作距离远、隐蔽性强、对敌方具有迷惑性等优点。正是由于无源测向定位系统的这些优点使其在侦察、预警探测等当代电子战中的主流应用领域发挥着越来越重要的作用[1],但同时测向精度也存在较大的提升空间。文献[2][3][4]分别通过矢量累积、研究来波方向的贝叶斯估计以及改变天线阵的结构来提升测向的精度,但均未考虑到目标自身的运动特性。
由于更多的系统是非线性模型,扩展卡尔曼滤波(EKF)是一种针对非线性系统的滤波算法,解决了传统卡尔曼滤波算法无法适用于非线性模型的难题。其核心思想是用泰勒公式将非线性函数按阶数展开,进行局部线性化,去掉高阶项后得到近似值[5][6]。
本文在原有相位干涉仪测向算法的基础之上,结合机动目标自身的运动特性,提出一种基于EKF的测向算法,经仿真表明新提出算法相比较常规相位干涉仪测向算法测向精度有了较大的提升。
1 相位干涉仪测向原理

图1.相位干涉仪测向基本原理
相位干涉仪测向是现今在实际中应用较为广泛的测向方式,其基本原理是利用不同测向天线在相同时刻接收到的信号相位差与信号的到达方位和仰角的关系来确定信号的方向。为了能更加直观的说明问题,在此本文只对机动目标产生信号在二维平面内的方位角的测向过程进行分析。
如上图1所示为相位干涉仪测向的基本原理[7],假设机动目标距天线位置足够远,由其产生的到达两个天线的信号可认为是平面波,可见,接收信号到达天线A1、A2相位差为
![]() (1)
(1)
其中,![]() 表示天线水平间距,
表示天线水平间距,![]() 表示接收信号波长,
表示接收信号波长,![]() 表示信号方位角,通过测得两天线间的相位差
表示信号方位角,通过测得两天线间的相位差![]() ,即可确定信号的方位角
,即可确定信号的方位角
![]() (2)
(2)
2 基于EKF针对机动目标的相位干涉仪测向算法
2.1 系统模型
在上图1的坐标系中,天线A1位置在坐标原点,且机动目标距天线位置足够远。在此假设机动目标做匀速直线运动,采样时间间隔为![]() 。在较短的时间内,根据被测目标运动特点建立系统状态方程[8],
。在较短的时间内,根据被测目标运动特点建立系统状态方程[8],
![]() (3)
(3)
其中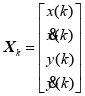 ,表示机动目标在
,表示机动目标在![]() 时刻的状态向量,
时刻的状态向量,![]() 、
、![]() 表示目标位置坐标,
表示目标位置坐标,![]() 、
、![]() 表示目标运动速度在X和Y轴上的分量,可得此时目标方位为
表示目标运动速度在X和Y轴上的分量,可得此时目标方位为![]() 。
。 ,表示
,表示![]() 时刻到
时刻到![]() 时刻的一步转移矩阵。
时刻的一步转移矩阵。 表示系统噪声驱动阵。
表示系统噪声驱动阵。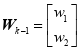 为系统激励噪声,
为系统激励噪声,![]() 。
。
根据相位干涉仪侧向算法,建立系统量测方程
![]() (4)
(4)
其中,观测量![]() ,
,![]() 表示经测量得到的两测向天线间的相位差。
表示经测量得到的两测向天线间的相位差。 ,其为非线性函数。
,其为非线性函数。![]() ,
,![]() ,
,![]() ,且与系统驱动噪声相互独立。
,且与系统驱动噪声相互独立。
2.2 算法流程
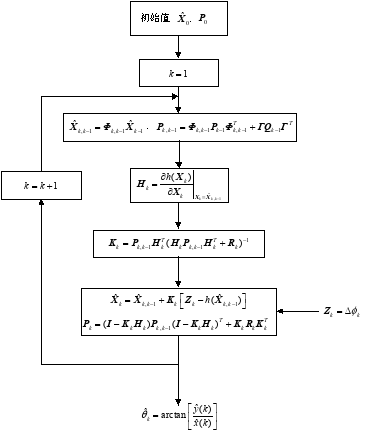
![]()
图2算法原理框图
从上述构建的系统模型可见系统的量测方程为非线性方程,所以本文采用扩展卡尔曼滤波(EKF)求解以上非线性方程。首先根据在![]() 时刻目标状态的估计值
时刻目标状态的估计值![]() ,得到
,得到![]() 时刻目标状态的一步预测值
时刻目标状态的一步预测值
![]() (5)
(5)
对公式(4)中函数![]() 围绕预测状态
围绕预测状态![]() 进行Taylor级数展开,并取一次近似,得到Jacobi矩阵
进行Taylor级数展开,并取一次近似,得到Jacobi矩阵![]() 。加入
。加入![]() 时刻观测量
时刻观测量![]() ,计算
,计算![]() 时刻目标状态的估计
时刻目标状态的估计
![]() (6)
(6)
估计误差为
![]() (7)
(7)
经由![]() 时刻目标状态估计
时刻目标状态估计 ,得到此时机动目标方位估计值
,得到此时机动目标方位估计值
![]() (8)
(8)
其中,滤波增益![]() ,一步预测误差
,一步预测误差![]() ,
,![]() 为
为![]() 时刻估计误差。
时刻估计误差。
基于EKF针对机动目标的相位干涉仪测向算法总体原理框图如上图2所示,目标初始状态为![]() ,初始估计误差为
,初始估计误差为![]() ,经鉴相或由其它方式得到
,经鉴相或由其它方式得到![]() 时两个测向天线间的相差
时两个测向天线间的相差![]() 作为量测量
作为量测量![]() ,经滤波得到
,经滤波得到![]() 时机动目标的方位估计
时机动目标的方位估计![]() 。
。
3 仿真分析
在如上图1所示的二维直角坐标系下,假设机动目标只在y>0的空间内运动且离天线位置足够远,天线A1在坐标原点,目标的起始位置为P(6km, 30km),运动速度在X轴和Y轴的分量分别为-24m/s和-18m/s,系统噪声方差为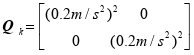 。机动目标发出信号载波频率为2.4GHz,天线间距d=0.1m,量测量两天线间相差
。机动目标发出信号载波频率为2.4GHz,天线间距d=0.1m,量测量两天线间相差![]() 为1s得到一组,量测噪声方差为
为1s得到一组,量测噪声方差为![]() ,在200s时间内,经100次蒙特卡洛仿真得到如下图3,4,5所示结果,其中由观测量
,在200s时间内,经100次蒙特卡洛仿真得到如下图3,4,5所示结果,其中由观测量![]() 直接经由常规相位干涉仪算法得到目标的方位信息为
直接经由常规相位干涉仪算法得到目标的方位信息为![]() 。
。

图3机动目标真实角度、经常规相位干涉仪算法得到观测角度和经本文提出算法得到的估计角度

图4上图3的局部放大

图5经常规相位干涉仪算法得到机动目标角度的观测误差和本文提出算法得到机动目标角度的估计误差对比
通过以上的仿真结果,可以看出本文提出的基于EKF针对运动目标的相位干涉仪测向算法较常规相位干涉仪测向算法测向误差有明显减小,测向精度有较大的提高。
参考文献:
[1]王国林. 长基线干涉仪测向关键技术研究[D]. 电子科技大学, 2014.
[2]LIANG Junli.Joint Azimuth and Elevation Direction Finding Using Cumulant[J].IEEE Sensors Journal,2009,9(4):690-698.
[3]Joshua M.Kantor,ChristD.Richmond.Mean-Squared-Error for Bayesian Direction of Arrival Estimation[J].IEEE Transaction on signal processing,2013,61(19):4729-4738
[4] Lee J H , Woo J M . Interferometer Direction-Finding System With Improved DF Accuracy Using Two Different Array Configurations[J]. IEEE Antennas & Wireless Propagation Letters, 2015, 14:719-722.
[5]王佳彬. 高频地波雷达飞行目标高度估计的研究[D]. 哈尔滨工业大学, 2011.
[6]秦永元, 张洪钺, 王叔华. 卡尔曼滤波与组合导航原理[M]. 西北工业大学出版社, 2012.
[7] Alejos A V , Garcia Sanchez M , Iglesias D R , et al. Performance analysis of angle persity for direction finding in 2.4 ghz tracking applications[J]. IET Communications, 2012, 6(2):147-0.
[8]郭福成. 基于运动学原理的单站无源定位与跟踪关键技术研究[D]. 国防科学技术大学, 2002.