多时滞广域测量电力系统稳定分析与协调控制器设计

多时滞广域测量电力系统稳定分析与协调控制器设计

钱局东

云南增股工程勘察设计有限公司  云南昆明650000

摘要：根据电力系统的时滞差异，可将其控制器信号大致划分为两类，其一是本地无时滞控制输入信号，其二则是异地多时滞控制输入信号，以此为基础可构建多时滞电力系统模型，并通过时滞分量的合理运用，将原本复杂的控制问题转化为相对直观易懂的现行矩阵不等式问题。此次在分析并设计多时滞电力系统控制器的基础上，结合仿真算例，论证该系统的应用有效性，以此能够为电力系统的多时滞控制提供实用且有效的方法，更加有效地保障电力系统的稳定与安全运行。

关键词：多时滞；广域测量；时滞分量；电力系统

前言：广域测量系统主要依托高速通信网络，在广域电网运行过程中，借助于相量测量单元采集其运行参数，并及时将参数传输至数据处理中心，从而实现对电力系统运行情况的动态、全面监控。将该系统运用至广域反馈信号控制中，可以显著改善互联系统动态性能。随着电网规模日益增大，在广域信息传输过程中，时滞有时会长至数百毫秒，对于系统稳定性造成的影响逐渐加大。而在工程控制领域中，自内点法被提出以来，线性矩阵不等式的应用价值明显提升，通过对控制问题的合理转化，能够借助于线性矩阵不等式相关知识与方法加以更好的解决。现有研究发现，基于时滞独立的系统稳定条件，能够设计出实用的状态反馈控制器；借助于线性矩阵不等式相关理论，则能够确定出时滞依赖的稳定性条件，进而设计出能够维护系统稳定的控制器；通过对广域时滞信号的有效利用，能够设计出广域自适应监视器，促进电力系统区域震荡阻尼的升高[1]。

不过目前，关于多时滞系统的控制设计，仍普遍依赖于固定的延迟时间常数，而对于本地信号无延迟的情况有所忽视。在此情况下，由于在不同通信传输通道的延迟时间有所差异，而且在其随机性特征影响下会引起电力系统的多时滞情况，若将所有控制输入信号都视为有延迟的情况，即便控制器性能较为优越，也很可能在电力系统中失效[2]。因此，在对广域控制信号进行分析时，有必要考虑其是否存在延迟以及具体的延迟参数，进而再为线性多时滞电力系统推导出适宜的稳定判据，最后根据相应的控制参数及最大时滞等数据，设计出实用的时滞控制器。

1 电力系统多时滞建模

1.1电力系统建模

结合多机电力系统特点，为其建立模型动态方程如公式（1）

①dδi/dt=ω0（ωi-1）；

②dωi-/dt=1/TJi·[Pmi-Pei-Di（ωi-1）]

③d/dt=1/·[--（xdi-）Idi+Efdi]        （1）

④dEfdi/dt=1/TAi（-Efdi-KAiUti+KAiVsi）

当达到平衡运行点时，对于向量xi=（Δδi，Δωi，Δ，ΔEfdi）T，可将其值定义为（Δδi0，Δωi0，Δ，ΔEfdi0）T，由此可推导，当多机电力系统位于平衡点时，其动态方程可如公式（2）所示，

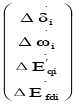=＋    （2）

其中，下表i指代第i台发电机，δ、ωi和ω0分别代表发电机的功角、角速度以及同步转速，xdi和分别代表轴的暂态电抗与同步电抗，代表暂态开路状态下的时间常数，代表发电机暂态电动势，Di则代表阻尼系数。以此为基础，当处于运行点附近且扰动较小时，多机电力系统方程可表示为公式（3）：

①（t）=A1x1（t）+B1u（t）

②y（t）=C1x1（t）                   （3）

其中，y指代电力系统的测量输出值，C1指代测量输出矩阵，在能够以状态空间形式表现时，可按如下公式（4）表示输出反馈控制器：

①（t）=Ak（t）＋BKy（t）

②u（t）=CK（t）+DKy（t）         （4）

其中代表控制的状态，AK、BK、CK、DK分别指代控制器中不同的参与矩阵，具体参数有待确定。

1.2多时滞电力系统建模

在闭环控制系统中，通常会设有至少两层控制系统，其一是本地阻尼控制，其二则是广域阻尼控制，二者均位于发电机励磁系统上[3]。设机组反馈信息产生的时滞为τij，其数值通常很小，当i=j时，τij=0，若时滞由广域信号产生，则i≠j。此时可将系统总反馈控制输入情况按如下公式（5）表示，而闭环时滞电力系统模型如公式（6）所示：

u（t）=uL（t-τij）+uW（t-τij）       （5）

（t）=Ax（t）+    （6）

2 多时滞分量的输出反馈控制器设计

2.1本地控制器设计

本地控制器将机组转数作为输出信号，该情况下的传输时滞值为零，可将其看作一般控制系统，并将电力系统模型以公式（7）表示：

（t）=A2x2（t）    （7）

2.2忽略时滞分量影响的广域控制器设计

在电力系统实际运行时，可参照公式（6）表示闭环状态下的系统模型，进而计算分析出控制器的参数矩阵，如公式（8）所示：

①DKW=；

②CKW=（MT）-1；

③BKW=N-1（-YB1DKW）；                 （8）

④A

KW=N-1（-YA2X）（MT）-1-N-1YB1DKW

2.3需要分析时滞分量影响的广域控制器设计

在多时滞系统中，若存在PT、RT两个参数的取值范围在0～Rn×n之间，且能够使如下公式（9）成立，则表明电力系统处于渐进稳定状态。

＜0      （9）

通过变量替换方法的应用，还可得出新变量的值[4]。在此基础上，基于变量间的替换关系，则可计算得出广域控制器中的参数矩阵，具体包括AKW、BKW、CKW、DKW。

3 仿真算例

为具体论证所设计控制器的有效性，此次引入如图1所示的两区域四机系统，每台发电机均配有励磁系统，图中G1和G3作为主导机组。

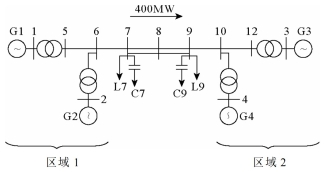
图1 两区域四机电力系统

在本地控制器应用中，系统全部特征值的实部均是负值，但系统中还是存在低频振荡区间，阻尼系数可达到0.1。对此，有必要通过增加广域阻尼的方式，以对区间低频振荡加以有效抑制。

在不考虑时滞分量的情况下，引入线性矩阵不等式理论，在对线性不等式可行性的求解过程中，便能够计算得出电力系统可接受的时滞最高值。当无广域控制器时，电力系统运行看似稳定，但对于低频振荡的控制效果并不理想；而在配置广域控制器时，最大时滞数值较高且系统不够稳定。由此，此次为广域控制器所提出的计算方法较为有效。

在考虑时滞后分量的情况下，随着时滞分量数值的不断升高，广域控制器的控制性能随之提升，不过与此同时，受时滞分量增加影响，线性矩阵不等式的求解难度也在升高。当时滞分量r=2时，控制器的控制效果最佳。因此，在为电力系统设计时滞控制器时，有必要对时滞分量的取值进行适当限制。

结语：此次根据多时滞电力系统常见的两种控制方式，构建出相对新颖且实用的系统模式，并结合线性矩阵方法，设计了包含时滞分量的多时滞控制器。该控制器的合理设计及有效运用，能够显著发挥出本地控制器的控制功能，并由时滞控制器提供辅助，对系统中的区域间振荡加以有效抑制。随着时滞分量的升高，系统保守性逐渐减小，广域控制器的性能发挥更加显著，但同时线性矩阵不等式的求解难度也会加大，因此在设计及应用中，应对合理设定时滞分量的取值范围，以促进多时滞控制器功能的充分发挥。

参考文献：

[1]郭建锋,钱伟,费树岷等.基于优化泛函的多时滞广域电力系统稳定性分析[J].电力系统保护与控制,2023,51(12):47-57.

[2]郭良栋,张旺.基于积分不等式的多时滞电力系统稳定性分析[J].辽宁科技大学学报,2021,44(06):470-476.

[3]彭思源.基于广域测量技术的电力系统时滞相关稳定性分析[D].湖南工业大学,2021.

[4]张慧,叶华,李常刚等.一种改进的时滞电力系统特征值高效计算方法[J].山东大学学报(工学版),2022,52(05):44-54.