变导引阶次的多约束二次型最优导引律

变导引阶次的多约束二次型最优导引律

牟安旭   宁方清   李欣   李贵栋

（江南机电设计研究所  贵州贵阳  550009）

摘 要：针对拦截机动目标需用过载较大的问题，研究一种含导引阶次n，在拦截初期令，拦截中后期的变导引阶次多约束二次型最优导引律。仿真结果表明，所设计的导引律不仅能保证拦截弹制导初期需用过载较小，且能在终端时刻保证需用过载及视线角速率收敛至0附近，同时能满足对攻击角的约束。

关键词：最优制导律；变导引阶次；攻击角约束；需用过载

0 引言

随着战场环境的愈加复杂，军事对抗手段的层出不穷，空袭作战手段的多变，作战模式的革新，使得传统防空武器系统面临极大地压力。为提升拦截机动目标的成功率，防空导弹需要采用适应机动目标的新型多约束导引律降低拦截过载需求，提升综合拦截能力。

针对某些目标为了满足一些特定的拦截需求，研究带角度约束的新型导引律尤为重要，而带角度约束的最优导引律是学者们研究的重点方向。Hexner等[1]基于线性二次最优控制理论和随机输入描述函数，将目标机动加速度建模视为一阶马尔科夫随机过程，设计了一种给定拦截弹最大加速度限制且考虑制导系数增益最大值限制的最优制导律。付主木等[2]针对静止目标并且要求拦截弹攻击方式为近似垂直俯冲，设计了一种同时考虑落角和落点约束的最优制导律。花文华等[3]设计了一种随机最优制导律，并设计了一种SOGL的补偿方法，来抑制目标机动过载估计所产生的滞后对系统的影响。从以上文献研究成果来看，最优制导律具有诸多优点如强鲁棒性和设计简单等，但是在实际制导过程中拦截弹前期过载较大，弹道较弯曲，会使拦截弹过早的用完自身能量，而在拦截末段不能成功的对目标进行有效的拦截。

针对上述问题，本文开展新型高精度制导方法的研究，研究一种含导引阶次n，通过改变n的大小即可改变二次型最优制导律制导系数的制导方法，研究该制导方法的导引阶次n与拦截弹性能之间的关系，最终设计出一种保证拦截弹制导初期过载不大且满足攻击角约束、视线角速率和过载能收敛到0附近的二次型最优制导方法。

1 弹目相对运动模型建立

平面内拦截过程中拦截弹与目标的相对运动关系如下图所示。其中，为拦截弹与目标间的相对距离；下标和分别表示拦截弹与目标；为弹道倾角，为视线角，是拦截弹与目标连线（目标线）与间的夹角。表示瞬时交会角，定义为拦截某瞬时导弹速度矢量与目标速度矢量反方向所夹的角度，通常称攻击角，能与视线角相互转换。

图1  二维平面内弹目运动关系图

由图可得如下方程：

(1)

(2)

(3)

式中，，。

令、，代入式（3）并将两式对时间求导，整理后得：

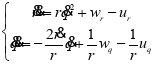（4）

其中，、分别表示拦截弹与目标加速度在目标线上的分量；、分别表示拦截弹与目标加速度在目标线法向上的分量。

2 变导引阶次的最优制导律设计

2.1 含导引阶次的多约束最优导引律

取相对位置与相对速度作为状态变量记为、，得如下方程组：

（5）

式中，与分别表示目标与拦截弹位置，与分别表示目标与拦截弹速度，与分别表示目标与拦截弹加速度。

状态方程为

（6）

状态空间表达式为

式中，，，，。

为了保证拦截弹能命中目标，则终端状态量；通过控制速度来满足对攻击角的约束，则终端状态量，因此终端状态量为：

（7）

设置如下二次型性能指标函数：

（8）

式中，为终端加权矩阵，为控制加权矩阵，。

由最优控制原理有：

（9）

为了得到适用于工程中的制导律，应用小角度假设原理，求解可得：

（10）

式中，，，为期望的终端视线角，为目标机动补偿系数。

2.2 变导引阶次的多约束最优导引律

导引阶次的取值直接影响着导弹的需用过载，当能保证拦截弹拦截初期需用过载以及全局需用过载最优，但是无法保证需用过载以及视线角速率在终端时刻收敛至0附近；当时能保证拦截弹在终端时刻需用过载以及视线角速率在终端时刻收敛至0附近，但在拦截初期会导致需用过载过大。因此在设计导引律时应考虑在拦截初期，拦截中末段。为了保证导引阶次能从0平稳的过渡到，引入线性过渡函数。引入过渡函数后导引阶次随时间变化的曲线如下图所示：

图 2  随时间变化曲线

上图中，时刻为拦截初始段，导引阶次，时刻为导引阶次过渡段，时刻为拦截中末段，导引阶次，由上图可得过渡段表达式为：

（11）

联立式（10）、式（11），得到考虑过渡函数的变导引阶次多约束二次型最优导引律如下：

（12）

3 仿真验证与分析

设定拦截弹初始位置为（0m，0m），速度为1000m/s，倾斜发射，弹道倾角为50°；设定目标初始位置为（m，m），目标速度为1200m/s，弹道倾角为-30°，设置目标高度在低于m做阶跃式变轨机动，机动大小；设置拦截弹无过渡函数时，导引阶次在时取0，在 后取1；有过渡函数时，导引阶次在时取0，在时为，在后取1；设置仿真步长为10ms，期望末端攻击角为0°。

图3为拦截轨迹，由图可知，拦截弹的弹道轨迹在拦截初期较为平直，且在引入过渡函数后，中段弹道轨迹更加平直。

图 3 拦截轨迹

图4、图5分别表示视线角速率变化曲线及过载变化曲线，从图4可看出，拦截弹视线角速率在终端时刻能收敛到一个不大的值，且引入过渡函数后变化更加平缓。由图5可知，拦截弹在拦截初期需用过载较小，并且在终端时刻能收敛到一个较小的值。当没有引入过渡函数时，其过载在5.04s时瞬间从0.9593g变到5.286g，这是不符合实际情况的，而在引入过渡函数后需用过载能进行平稳的过渡。

图 4  视线角速率                             图 5 过载曲线

是否引入过渡函数的脱靶量、能量以及最终与期望攻击角角的偏差如表1所示

表1 脱靶量、能量和攻击角偏差

由表1可知，对于机动目标的拦截，当引入过渡函数后，拦截弹的制导精度更高，对于末端时刻所期望攻击角的偏差更小，同时拦截弹的所消耗能量更小。

4 结束语

针对高机动目标拦截面临的需用过载较大的问题，设计出一种保证拦截弹制导初期过载不大且满足攻击角约束、视线角速率和过载能收敛到0附近的二次型最优制导方法。由上述仿真结果可知，对于所设计的变导引阶次的多约束二次型最优导引律，不仅能保证拦截弹制导初期需用过载较小，且能满足偏差较小的攻击角约束和较高的制导精度，其整体需用过载也有所降低，另外终端视线角速率和过载也能收敛到较小的值，对于拦截弹的各项性能都有着显著的提升。

参考文献：

[1]Hexner G, Pila A. Practical stochastic optimal guidance law for bounded acceleration missiles[J]. Journal of Guidance, Control, and Dynamics, 2011,34(2):437-445.

[2]付主木, 曹晶, 张金鹏. 带落角和落点约束的空地导弹最优制导律设[J]. 航空兵器, 2014, (1):3-6

[3]花文华, 孟庆龄, 张金鹏. 有界控制导弹随机最优制导律[J].固体火箭技术,2015, 38(1): 7-12.