1国网福建省电力有限公司,福建 福州 350003; 2国网福建省电力有限公司经济技术研究院,福建 福州 350003; 3福建省电力勘测设计院有限公司,福建 福州 350003
摘要:微电网通过并联变换器进行增容扩容时,由于其线路阻抗间存在偏差,导致有功/无功耦合,影响下垂控制性能和效果,产生环流增大系统功率损耗。对此,本文提出基于自抗扰控制技术(ADRC)的分段式虚拟阻抗改进下垂控制策略,以正负序与额定电压、实时与额定无功功率的偏差为基础,分别设计关于虚拟阻抗的分段函数,构成基于电压偏差和无功偏差的改进下垂控制,跟踪监测电压和无功;为阻止因虚拟阻抗接入引起的电压跌落,提出基于ADRC的电压二次补偿策略,通过跟踪直流母线参考电压和额定电压,实时更新二次电压补偿值。最后,选取两并联变换器系统为研究对象,基于Matlab/Simulink仿真分析,结果表明:本文所提改进下垂控制策略在改善环流和补偿电压跌落方面效果明显,具有较好的工程适用性。
0 引言
为落实“双碳”战略和“以新能源为主体的新型电力系统”建设目标,新能源将逐步成为主体电源[1]。然而,风电、光伏等可再生能源机组出力具有间接性和波动性,随着其装机规模不断增加,对电力系统的影响愈发呈现复杂、多变、不稳定态势[2]。针对此问题通常整合多个分布式能源(distributed generator, DG)以微电网的形式接入系统[3]。而交流微电网(AC microgrid, AC MG)作为一种高效利用分布式能源方式,由于其灵活性和供电可靠性在近年来得到快速发展。
系统扩容主要方式有增大单台变换器容量和并联变换器两种。因增大单台变换器容量易受电力电子器件、电磁干扰等因素影响,通常会选用并联变换器的方式[4,5]。下垂控制因其具有较高的可靠性、即插即用性以及便于系统扩容等特点[6-10],成为变换器并联的主流控制策略[11]。下垂控制在双闭环的基础上加入功率外环,可以实现并联变换器的自主功率共享,但变换器间的等效阻抗对整个系统功率分配存在显著影响,致使系统中负荷分配不均,从而产生环流,且环流越大,变换器功率损耗将会越大[12,13],同时下垂控制还存在下垂系数过大造成母线电压跌落,下垂系数过小影响功率分配精度等问题[14]。
为解决环流和母线电压跌落的问题,常用方法是引入虚拟阻抗和注入交流信号。引入虚拟阻抗即改变下垂系数[15-17]并配合二次电压补偿法[18],通过引入虚拟阻抗可以调整变换器的等效阻抗,减小线路阻抗差,来解决环流和母线电压跌落之间的矛盾。文献[19]提出一种混合奇数阶分段非线性下垂系数法及其多项式平滑拟合表达式,并形成基于ADRC的电压偏差二次补偿方案;文献[20]提出一种自适应虚拟阻抗法,引入交流母线电压反馈,将等效下垂控制曲线设计为非线性函数,从而协调功率均分精度与输出电压跌落之间的内在矛盾,抑制环流;文献[21]在传统下垂控制基础上,根据光伏侧变流器输入电压偏差对下垂系数进行修正,实现不同功率裕度光伏电源之间不平衡功率的合理分配;文献[22]通过检测变换器输出端口的电压偏差,对下垂控制系数进行修正,显著降低并联变换器间的环流;文献[23]通过在逆变器下垂控制环节增加降电压来调节输出电压,跟随主逆变器电压参考值,实现下垂控制在双并联逆变器上的性能提升。上述研究在环流控制方面取得了显著效果,一定程度上满足工程适用性,若进一步考虑无功功率对环流的影响,环流控制精度将会进一步得以提升。此外,线路阻抗随变换器容量增大而增大,但下垂系数选取受最大电压偏差限制,难以通过继续增加下垂系数方式来获取理想的电流分配效果。
基于上述研究基础和面临问题,本文结合变系数下垂控制和ADRC二次电压补偿,提出一种基于ADRC的分段式虚拟阻抗改进下垂控制策略,采用U_I和Q_U相结合的下垂控制方式来提高控制精度。首先,结合无功功率偏差和电压偏差分别拟合虚拟阻抗的分段函数,来实时调整下垂控制系数,以降低环流值;其次,采用自抗扰控制技术(ADRC)对额定电压和直流母线电压参考值实时跟踪,在降低变换器间环流值的同时,电压跌落得以补偿;最后,建立两台变频器并联系统模型,通过设置参数来改变变频器主电路之间的参数差,验证本文所提改进下垂控制策略在改善环流和补偿电压跌落方面的优势。
1 下垂控制特性分析
变换器是风电等新能源发电机组的重要组成部分,本文选取交流微电网作为研究对象,通过对微网模型进行简化,搭建由两台1.5MW变频器并联扩容组成的3MW系统,
下垂控制主要应用在电压环之前,计算电压环PI控制器所需的直流母线电压参考值。经电压电流双闭环控制后,对变换器进行控制,其控制框图如图1所示。
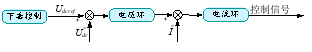 图1 变换器控制框图
图1 变换器控制框图
Fig. 1 converter control block diagram
通过基于U_I控制和Q_U的下垂控制分析可知,变换器间环流不仅与并联变换器线路阻抗有关,还与变换器两端电压有关,可通过减小并联变换器输出电压偏差和并联变换器线路阻抗偏差来减少两变换器之间的环流。
12基于分段虚拟阻抗改进下垂控制
在传统下垂控制中,为避免线路阻抗不同影响无功功率分配,常用解决方法是在变换器输出端串入硬件电感,使变换器整体呈感性,但会增加成本和线路损耗。虚拟阻抗技术从软件上改变变换器等效阻抗形式来解决环流问题,一定程度上降低成本和线路损耗。现有基于虚拟阻抗的改进下垂控制,多是仅通过电压或无功来确定虚拟阻抗值。
对此,本文综合考虑变换器输出端口电压差异和无功功率差异以及下垂系数选取的约束,将下垂控制输出分为以实时电压偏差为控制对象的U_I下垂控制输出、以实时无功偏差为控制对象的Q_U下垂控制输出及电压参考基础值三部分,既能保证下垂系数不越限又能多方面考虑环流影响因素,提高环流控制精度。控制框图如图2所示:

图2改进下垂控制框图
Fig.2. Improved droop control block diagram
1.1基于电压偏差改进下垂控制
由分析可知,环流受并联变换器输出端口电压偏差和线路阻抗偏差影响,为获得精确的控制效果,本文采用变换器输出端口电压和额定电压进行比较,由其电压比值拟合下垂控制系数的分段函数。考虑到谐波对控制效果的影响,采用变换器输出端口正负序电压,经均值滤波器滤波后作为改进下垂控制输入。
对基于二阶广义积分正负序分离模块进行建模,并联变换器输出端口的电压进行正负序分解,经均值滤波器作为下垂控制输入,与额定电压之间的偏差关系即电压偏差率,来确定![]() 的值。下垂控制的框图如下图3所示:
的值。下垂控制的框图如下图3所示:
![]() 图3基于正负序分解改进下垂控制逻辑框图
图3基于正负序分解改进下垂控制逻辑框图
Fig.3 Improved droop control logic block diagram based on positive and negative order decomposition
其中,下垂系数由正负序电压和变换器输出电压额定值之间的偏差来确定。通过反复仿真验证,可以得到![]() 的表达式为:
的表达式为:
 (1)
(1)
式中,![]() ,为变换器输出正负序电压之和;
,为变换器输出正负序电压之和;![]() 、
、![]() 、
、![]() 为正值常数。
为正值常数。
在下垂控制中,采用正负序分解的方式进行控制,可抑制谐波影响。根据分析可知,引入虚拟阻抗可减少两变换器间的环流,采用分段形式的下垂控制表达式,能够保证虚拟阻抗值随电压波动而变化,从而实现在电网电压发生突变(电压过高或过低)时,能根据电压变化采用不同的参数进行实时调整。
1.2基于无功功率偏差改进下垂控制
由分析可知,并联变换器间的环流受无功功率的影响,所以本文在Q_U下垂控制基础进行改进,根据分布式电源额定容量和功率因数计算额定无功功率:
![]() (2)
(2)
式中:![]() 为变换器功率因数;
为变换器功率因数;![]() 为变换器额定有功功率。根据变换器实时无功功率指令
为变换器额定有功功率。根据变换器实时无功功率指令![]() (n=1、2)与额定无功功率之间的关系确定下垂控制系数,则下垂控制的表达式为:
(n=1、2)与额定无功功率之间的关系确定下垂控制系数,则下垂控制的表达式为:
![]() (3)
(3)
则改进下垂控制的结构框图如图4所示:
 图4 基于瞬时无功功率改进下垂控制
图4 基于瞬时无功功率改进下垂控制
Fig.4 Improved droop control based on instantaneous reactive power
通过上述方式引入虚拟阻抗,以降低线路阻抗偏差值,而两变换器间的环流减少,无功功率分配不均的情况得以改善。
综合考虑由电压偏差和无功功率偏差控制得到的直流母线电压给定值变化量,确定下垂控制输出的直流母线电压给定值,其表达式为:
![]() (4)
(4)
式中:![]() (n=1、2)为直流母线电压给定值、
(n=1、2)为直流母线电压给定值、![]() 为直流母线电压参考基础值。
为直流母线电压参考基础值。
本文提出的改进下垂控制同时考虑缩小并联变换器间线路阻抗偏差和电压偏差,从而提高了下垂控制对环流的控制精度,且跟踪电压和无功功率来实时调整虚拟阻抗,使得变换器在不同工况运行时,均可达到控制精度要求。同时,由于采用偏差值,避免下垂系数越限的情况。然而,引入虚拟阻抗使变换器输出电压发生跌落,需要对由虚拟阻抗引起的电压跌落进行补偿。
2基于自抗扰控制技术的二次电压补偿
由上述分析可知,引入虚拟阻抗改变变换器线路阻抗偏差,实现有功/无功功率解耦,降低两变换器间的环流。引入虚拟阻抗相当于在电压闭环控制中加入虚拟阻抗的负反馈环节,通过d轴电流与虚拟阻抗相乘,并作用到电压环的输入端,从而造成变换器输出端的电压产生一定的跌落,且虚拟阻抗值越大,电压跌落越大。
因此,需要在式(4)基础上加入二次电压补偿控制策略,补偿器可根据电压追踪信息快速生成补偿信号以抑制扰动,同时二次电压补偿保证了直流母线电压在发生波动情况下电压的一致性,其表达式为:
![]() (5)
(5)
式中:![]() (n=1、2)为变换器二次电压补偿值。
(n=1、2)为变换器二次电压补偿值。
所以其总体控制框图如图5所示。
 图5改进下垂控制整体控制框图
图5改进下垂控制整体控制框图
Fig.5 Overall control block diagram of improved droop control
由于自抗扰控制技术(ADRC)具有结构简单、适用面广、不依赖于模型、控制效果好、鲁棒性强、便于调试的特点,非常适于由引入虚拟阻抗引起电压跌落的补偿。
ADRC的结构组成如下图6所示。
 图6 ADRC结构图
图6 ADRC结构图
Fig.6 ADRC structure diagram
由于变换器采用电压电流双闭环控制的方式,在电压环中采用PI控制,其输入输出为一阶惯性环节,为电压环的输入,电压环整定框图如图7所示。
 图7 电压环整定框图
图7 电压环整定框图
Fig.7 Voltage loop setting block diagram
其中,![]() 为采样、滤波环节的等效时间常数,2T为电流内环等效时间常数,
为采样、滤波环节的等效时间常数,2T为电流内环等效时间常数,![]() 为转换环节系数,取0.75;C为控制对象参数。
为转换环节系数,取0.75;C为控制对象参数。
由于变换器双闭环控制输入为一阶惯性环节,可采用一阶自抗扰控制技术对电压跌落进行补偿。根据自抗扰理论,ADRC主要由一阶非线性跟踪微分器(first-order nonlinear tracking differentiator, FONTD)、二阶扩张状态观测器(extended state observer, ESO)和非线性状态误差反馈控制律(nonlinear state error feedback, NLSEF)三部分组成[19]。
2.1一阶非线性跟踪微分器
一阶非线性跟踪微分器主要是安排过渡过程,在用于电压补偿中时,则是为变换器输出电压额定值安排过渡过程,实现对变换器输出电压额定值的实时跟踪,即![]() ,
,![]() 为跟踪偏差,
为跟踪偏差,![]() ,则跟踪的动态过程为:
,则跟踪的动态过程为:
![]() (6)
(6)
式中,![]() 为跟踪微分器的增益(为正数)、
为跟踪微分器的增益(为正数)、![]() 为滤波因子,其中
为滤波因子,其中![]() 。
。
为实现能够根据滤波因子![]() 和跟踪偏差
和跟踪偏差![]() 的大小关系进行区分计算,发挥小偏差使用较大增益,大偏差采用较小增益的优良非线性特点,采用
的大小关系进行区分计算,发挥小偏差使用较大增益,大偏差采用较小增益的优良非线性特点,采用![]() 为非线性组合幂次函数,其表达式为:
为非线性组合幂次函数,其表达式为:
 (7)
(7)
式中,![]() 为非线性因子,其中
为非线性因子,其中![]() ,本文设定为0.5;
,本文设定为0.5;![]() 为滤波因子,其中
为滤波因子,其中![]() ,本文设定为0.1。
,本文设定为0.1。
根据上式可以看出,![]() 能够实现对额定电压的实时跟踪,且
能够实现对额定电压的实时跟踪,且![]() 越大,过渡过程越快。
越大,过渡过程越快。
2.2二阶扩张状态观测器
二阶扩张状态观测器主要用来对输出信号和外部干扰的实时观测,其表达式为:
![]() (8)
(8)
式中,![]() 直流母线电压参考值
直流母线电压参考值![]() (二次补偿前)(n=1,2)的信号跟踪;
(二次补偿前)(n=1,2)的信号跟踪;![]() 为未知扰动
为未知扰动![]() 的观测信号;
的观测信号;![]() 为跟踪误差,其中
为跟踪误差,其中![]() ;
;![]() 和
和![]() 为输出的校正误差正增益,
为输出的校正误差正增益,![]() (
(![]() )为控制增益。
)为控制增益。
其中式(8)是与对象模型和外干扰作用无耦合关系的连续非线性观测器,具有对模型强适应性、有限时间收敛速度快且无振荡的特点[24]。因此,根据式(8)构建二阶特征方程,采用极点配置法,选择合适的校正误差正增益![]() 和
和![]() ,可使ESO各状态变量较好的跟踪直流母线电压参考值及扰动量。
,可使ESO各状态变量较好的跟踪直流母线电压参考值及扰动量。
2.3非线性状态误差反馈控制率
非线性状态误差反馈控制律是用过渡过程与ESO状态观测之间误差的非线性组合和扰动估计量的补偿来生成控制信号,可表达为:
![]() (9)
(9)
式中:状态误差![]() ,
,![]() ;
;![]() 和
和![]() 为非线性组合正增益。
为非线性组合正增益。
由于![]() 为变换器输出电压额定值的微分量,因此,控制律中非线性组合正增益相当于PD控制器中的比例系数和微分系数,和传统PD控制器的整定方式相同。根据上述分析,基于自抗扰控制技术的二次电压补偿可以写为:
为变换器输出电压额定值的微分量,因此,控制律中非线性组合正增益相当于PD控制器中的比例系数和微分系数,和传统PD控制器的整定方式相同。根据上述分析,基于自抗扰控制技术的二次电压补偿可以写为:
![]() (10)
(10)
3仿真模型介绍
本文均采用单台1.5MW的变频器,其拓扑结构如图8所示。
 图8单个变频器的拓扑结构图
图8单个变频器的拓扑结构图
Fig.8Topological structure diagram of a single frequency converter
其中,![]() 、
、![]() 、
、![]() 分别为三相变换器电压;
分别为三相变换器电压;![]() 、
、![]() 、
、![]() 分别为三相电网电压;
分别为三相电网电压;![]() 、
、![]() 、
、![]() 分别为三相变换器电流;
分别为三相变换器电流;![]() 、
、![]() 分别为网侧进线等效电阻值和滤波电感;
分别为网侧进线等效电阻值和滤波电感;![]() 、
、![]() 分别为机侧等效电阻值和滤波电感;
分别为机侧等效电阻值和滤波电感;![]() 、
、![]() 分别为机侧LC滤波器电阻值和电容值。
分别为机侧LC滤波器电阻值和电容值。
变频器控制主要分为网侧控制和机侧控制两部分。其中,网侧控制主要包括直流母线电压控制、电压-电流双闭环控制及高低压穿越控制等,机侧控制主要包括转矩控制、磁链观测等部分组成。
下垂控制输出直流母线电压参考值,作为变频器网侧控制中电压环的输入参与到变频器控制。其主电路参数值为表1所示:
表1变频器主电路参数 | |||
Tab.1 Main circuit parameters of frequency converter | |||
参数名 | 数值 | 参数名 | 数值 |
网侧LC滤波器电感值Lg | 0.12e-3H | 机侧LC滤波器电感值Ls | 0.03e-3H |
网侧进线等效电阻值Rg | 9.4248e-4Ω | 机侧等效电阻值Rls | 2.3562e-4Ω |
机侧LC滤波器电容值Cs | 47e-9F | 机侧LC滤波电阻值Rcs | 20Ω |
本文采用由两台变频器并联容量为3MW和四台变频器并联容量为6MW的大容量系统进行仿真验证,其中两台变频器并联的拓扑图为:
 图9 两台变频器并联拓扑图
图9 两台变频器并联拓扑图
Fig.9 Parallel topology of two converters
其中,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 为变频器主电路参数的系数,变化范围为[0.5,1.5],通过
为变频器主电路参数的系数,变化范围为[0.5,1.5],通过![]() 的变化来控制两变换器参数差异。
的变化来控制两变换器参数差异。
4系统仿真与验证
4.1参数设置
为验证本文所提改进下垂控制方法可行性和电压补偿有效性,在Matlab/Simulink平台建立两台变换器并联模型和四台变换器并联系统模型进行仿真验证。其中,系统参数设置如表2所示。
自抗扰控制器中
FONTD、ESO和NLSEF的3个组成部分功能相互独立,采用分离性原则分别进行参数整定设计。可根据ADRC的理论分析和参数整定原则进行参数取值范围的确定,并经过多次仿真分析确定最佳参数取值。
基于电压偏差改进下垂控制部分为确保在电压波动时能够实时调整直流母线电压参考值输出。根据正负电压值与额定电压的比值拟合直流母线电压参考值输出曲线,在一定的范围内比值越大输出值越大,经过多次仿真验证确定![]() 、
、![]() 、
、![]() 的最优值。
的最优值。
表2 变换器并联系数相关参数 | |||
Tab.2 parameters related to the parallel coefficient of the converter | |||
参数名称 | 参数值 | 参数名称及单位 | 参数值 |
a1 | 40 | 跟踪微分器的增益β11 | 22 |
a2 | 60 | 滤波因子σ | 0.1 |
a3 | 100 | 非线性因子ρ | 0.5 |
非线性组合正增益β0 | 1.85 | 非线性组合正增益β1 | 8 |
控制增益b | 0.6 | 输出的校正误差正增益β21 | 2e-3 |
输出的校正误差正增益β22 | 7 | 滤波时间常数 | 0.004 |
4.2仿真验证
5.2.1 两台变换器并联系统仿真验证
为验证并联变换器主电路参数不一致时,改进下垂控制的有效性,首先在两个相同容量的变换器并联系统中进行仿真验证,通过改变![]() 值来控制变换器2与变换器1之间主电路参数的差异。
值来控制变换器2与变换器1之间主电路参数的差异。
A、环流仿真验证
在使用本文提出的改进下垂控制方法,仿真验证了在![]() 值在[0.5,1.5]之间变化时的环流波形,如图10所示。
值在[0.5,1.5]之间变化时的环流波形,如图10所示。
 图10 两变换器之间的环流值
图10 两变换器之间的环流值
Fig.10 Circulation values between two converters
通过图10可以看出,当![]() 值为1时,环流值最小,随着
值为1时,环流值最小,随着![]() 值的逐渐增大和减小环流值逐渐增大,但是都在可接受的范围内。其中当
值的逐渐增大和减小环流值逐渐增大,但是都在可接受的范围内。其中当![]() 时,环流值最大,此时两个变换器的电流及环流波形如图11所示。环流与两变换器电流相比很小,环流峰值为两变换器电流峰值的7.5%。
时,环流值最大,此时两个变换器的电流及环流波形如图11所示。环流与两变换器电流相比很小,环流峰值为两变换器电流峰值的7.5%。
 图11 两变换器输出电流及环流
图11 两变换器输出电流及环流
Fig.11 Output current waveform and circulation of two converters
在采用传统下垂控制,仿真验证![]() 值在[0.5,1.2] 之间变化时,两变换器之间的环流如图12所示。
值在[0.5,1.2] 之间变化时,两变换器之间的环流如图12所示。
 图12 两变换器之间的环流值
图12 两变换器之间的环流值
Fig.12 Circulation values between two converters
通过图12可知,当![]() 即两变换器线路阻抗完全相同时,由于阻抗差为0,所以环流值最小;但是随着
即两变换器线路阻抗完全相同时,由于阻抗差为0,所以环流值最小;但是随着![]() 值不断减小即减小变换器2线路阻抗值时,环流值也不断增大;但当
值不断减小即减小变换器2线路阻抗值时,环流值也不断增大;但当![]() 即增大变换器2线路阻抗时,由于下垂系数过大使两变换器间的环流突增。
即增大变换器2线路阻抗时,由于下垂系数过大使两变换器间的环流突增。
当![]() 时,两个变频器间的环流如图13所示,说明在两个变换器主电路参数完全相同时,本文所提基于ADRC的分段式虚拟阻抗改进下垂控制与传统下垂控制都具有较好的控制效果。
时,两个变频器间的环流如图13所示,说明在两个变换器主电路参数完全相同时,本文所提基于ADRC的分段式虚拟阻抗改进下垂控制与传统下垂控制都具有较好的控制效果。
 图13
图13 ![]() 时,两变换器之间的环流值
时,两变换器之间的环流值
Fig.13 Circulation value between two converters when![]()
其中,当![]() 时,本文提出的改进下垂控制和传统下垂控制的环流波形如图14所示。
时,本文提出的改进下垂控制和传统下垂控制的环流波形如图14所示。
 图14
图14 ![]() 时,两变换器之间的环流值
时,两变换器之间的环流值
Fig.14 Circulation value between two converters when![]()
如上图所示,当![]() 时,两种控制方法下变频器间的环流差距不大,改善不明显。
时,两种控制方法下变频器间的环流差距不大,改善不明显。
但是,当![]() 时,其变换器间的环流对比如图15所示。
时,其变换器间的环流对比如图15所示。

图15![]() 时,两变换器之间的环流值
时,两变换器之间的环流值
Fig.15 Circulation value between two converters when![]()
由于变换器主电路参数增大,导致采用传统下垂控制的变换器间环流突增,失去稳定性,而采用本文改进下垂控制的变换器,系统仍然稳定,且变换器间的环流仍在可控范围内。
当![]() 时,采用基于ADRC的分段虚拟阻抗改进下垂控制的并联系统中,环流仍然在可控制的范围内,如图16所示。但采用传统下垂控制的并联系统中在
时,采用基于ADRC的分段虚拟阻抗改进下垂控制的并联系统中,环流仍然在可控制的范围内,如图16所示。但采用传统下垂控制的并联系统中在![]() 时,系统就已经失稳。通过仿真验证表明,本文提出的改进下垂控制的方法具有更好的鲁棒性。
时,系统就已经失稳。通过仿真验证表明,本文提出的改进下垂控制的方法具有更好的鲁棒性。
 图16
图16 ![]() 时,采用改进下垂控制的环流
时,采用改进下垂控制的环流
Fig.16 Circulation with improved droop control at ![]()
B、电压偏差仿真验证
为验证变换器主电路参数不同的情况下,采用本文提出的改进下垂控制对电压跌落的补偿情况,![]() 值在[0.5,1.5]之间变化,其输出的A相电压波形与
值在[0.5,1.5]之间变化,其输出的A相电压波形与![]() 值的关系如图17所示。
值的关系如图17所示。
 图17变换器输出A相电压波形
图17变换器输出A相电压波形
Fig.17 Output A-phase voltage waveform of converter
由上图可知,当![]() 值在[0.5,1.5]之间变化时,电压幅值基本保持不变。图18为变换器A相电压的波形的右视图,由右视图可以看出,当
值在[0.5,1.5]之间变化时,电压幅值基本保持不变。图18为变换器A相电压的波形的右视图,由右视图可以看出,当![]() 值变化时,电压幅值基本没有变化。
值变化时,电压幅值基本没有变化。
 图18 变换器输出A相电压右视图
图18 变换器输出A相电压右视图
Fig.18 Right view of A phase voltage output of the converter
由图17、图18分析可知,采用本文提出的改进下垂控制,能够有效的补偿由于引入虚拟阻抗造成的电压跌落。
仿真结果表明,本文提出的改进下垂控制可有效控制变换器之间的环流,同时改善输出电压跌落问题。较传统下垂控制,在变换器主电路参数方面具有较好的参数鲁棒性,同时在多台变频器并联情况下也可较好的控制环流和输出电压跌落,证明了此算法具备较好的适用性。
5结论
本文基于2变换器并联系统对额定无功功率和实际无功功率偏差、正负序电压和额定电压之间的关系进行深入分析,构建了基于ADRC的电压二次补偿策略,通过Matlab/Simulink仿真验证了基于ADRC的分段虚拟阻抗改进下垂控制策略的可行性。基于本文研究得出以下结论:
1)同时考虑U_I下垂控制曲线和Q_U下垂控制曲线较单一采用其中一种在抑制环流精度方面改善明显;
2)基于电压偏差和无功功率偏差的下垂控制较基于电压和无功功率的下垂控制在控制精度方面显著提高;
3)采用自抗扰控制技术(ADRC)对直流母线电压参考值实时跟踪,进行母线电压二次补偿,具有适应性强、对模型参数不敏感等特点,实现对母线电压鲁棒、精确控制。
随着新型电力系统逐步发展,微电网容量也会逐步增大,下垂控制应用范围也会逐步扩展,但其下垂系数确定仍存在诸多挑战。后续研究中将尝试运用模糊控制、强化学习等先进优化算法对下垂系数进行寻优,保证下垂控制在环流和母线跌落抑制方面高效应用。
参考文献
[1]乐健, 周谦, 王曹, 等. 基于分布式协同的配电网电压和功率优化控制方法研究[J]. 中国电机工程学报,2020, 40(04): 1249-1257.
LE Jian, ZHOU Qian, WANG Cao, et al. Research on distributed collaborative voltage and power optimization control methods for distribution networks[J]. Proceedings of the CSEE,2020, 40(04): 1249-1257(in Chinese).
[2]刘向实, 王凌纤, 吴炎彬, 等. 计及配电网运行风险的分布式电源选址定容规划[J]. 电工技术学报,2019, 34(S1): 264-271.
LIU Xiangshi, WANG Lingxian, WU Yanbin,et al. Locating and Sizing Planning of Distributed Generation Power Supply Considering the Operational Risk Cost of Distribution Network[J].2019, 34(S1): 264-271(in Chinese).
[3]王灿, 邓灿, 潘学伟, 等. 基于线路阻抗补偿的互联变流器控制策略[J]. 电力系统自动化,2021.
WANG Can, Deng Can, Pan Xuewei,et al.Interconnection converter control strategy based on line impedance compensation[J]. .Automation of Electric Power Systems,2021,Chinese).
[4]Khan Rafid Adnan, Mahmood M. Rezwanul, Haque Anisul. Enhanced energy extraction in an open loop single-axis solar tracking PV system with optimized tracker rotation about tilted axis[J]. Journal of Renewable and Sustainable Energy, 2018, 10(4):45301.
[5]张巧杰, 余巧, 王久和, 等. 基于分段式虚拟阻抗的改进下垂控制[J]. 电力系统及其自动化学报,2021.
ZHANG Qiaojie YU Qiao WANG Jiuhe. An Improved Droop Control Based on Piecewise Virtual Impedance[J]. Proceedings of the CSU-EPSA,2021,Chinese).
[6]Dragicevic Tomislav, Guerrero Josep M., Vasquez Juan C.,et al. Supervisory Control of an Adaptive-Droop Regulated DC Microgrid With Battery Management Capability[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS, 2014, 29(2):695-706.
[7]Wang Panbao, Lu Xiaonan, Yang Xu,et al. An Improved Distributed Secondary Control Method for DC Microgrids With Enhanced Dynamic Current Sharing Performance[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS, 2016, 31(9):6658-6673.
[8]Mírez J. A Review of Droop Control Implementation in Microgrids[C]//2019 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE). IEEE, 2019: 146-150.
[9]杨捷, 金新民, 吴学智, 等. 一种适用于直流微电网的改进型电流负荷分配控制策略[J]. 中国电机工程学报报,2016, 36(1): 59-67.
YANG Jie , Xinmin JIN, Xuezhi W. U.,et al. An Improved Load Current Sharing Control Method in DC Microgrids[J].Proceedings of the CSEE,2016, 36(1): 59-67(in Chinese).
[10]季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报,2018, 33(2): 370-379.
JI Yu, WANG Dongxu, WU Hongbin,et al. The Active Damping Method for Improving the Stability of DC Microgrid[J]. Transactions of China Electrotechnical Society,2018, 33(2): 370-379(in Chinese).
[11]Wai Rong-Jong, Zhang Quan-Quan, Wang Yu. A Novel Voltage Stabilization and Power Sharing Control Method Based on Virtual Complex Impedance for an Off-Grid Microgrid[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS, 2019, 34(2):1863-1880.
[12]刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报,2019, 34(4): 795-806.
LIU Ziwen, MIAO Shihong, FAN Zhihua,et al. Accurate Power Allocation and Zero Steady-State Error Voltage Control of the Islanding DC Microgird Based on Adaptive Droop Characteristics[J]. Transactions of China Electrotechnical Society,2019, 34(4): 795-806(in Chinese).
[13]吕振宇, 吴在军, 窦晓波, 等. 自治直流微电网分布式经济下垂控制策略[J]. 中国电机工程学报,2016, 36(4): 900-910, 1199.
LV Zhenyu, WU Zaijun, DOU Xiaobo,et al. A Distributed Droop Control Scheme for Islanded DC Microgrid Considering Operation Costs[J]. Proceedings of the CSEE,2016, 36(4): 900-910, 1199(in Chinese).
[14]Beerten Jef, Belmans Ronnie. Analysis of Power Sharing and Voltage Deviations in Droop-Controlled DC Grids[J]. IEEE TRANSACTIONS ON POWER SYSTEMS, 2013, 28(4):4588-4597.
[15]Tah Avisha, Das Debapriya. An Enhanced Droop Control Method for Accurate Load Sharing and Voltage Improvement of Isolated and Interconnected DC Microgrids[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3):1194-1204.
[16]Xiao Jianfang, Setyawan Leonardy, Wang Peng,et al. Power-Capacity-Based Bus-Voltage Region Partition and Online Droop Coefficient Tuning for Real-Time Operation of DC Microgrids[J]. IEEE TRANSACTIONS ON ENERGY CONVERSION, 2015, 30(4):1338-1347.
[17]Chen Fang, Burgos Rolando, Boroyevich Dushan,et al. Investigation of Nonlinear Droop Control in DC Power Distribution Systems: Load Sharing, Voltage Regulation, Efficiency, and Stability[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS, 2019, 34(10):9404-9421.
[18]朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报,2018, 38(01): 72-84.
ZHU Shanshan, WANG Fei, GUO Hui,et al.Review of DC microgrid sag control technology research[J].Proceedings of the CSEE,2018, 38(01): 72-84(in Chinese).
[19]茅靖峰, 张珍梦, 吴爱华, 等. 基于ADRC的直流微电网混合奇数阶非线性下垂控制[J]. 高电压技术,2020, 46(07): 2296-2306.
MAO Jingfeng ZHANG Zhenmeng WU Aihua. Research on Hybrid Odd-order Nonlinear Droop Control for DC Microgrids Based on ADRC[J]. High Voltage Engineering,2020, 46(07): 2296-2306(in Chinese).
[20]陈杰, 刘名凹, 陈新, 等. 基于下垂控制的逆变器无线并联与环流抑制技术[J]. 电工技术学报,2018, 33(07): 1450-1460.
CHEN Jie LIU Mingao ,Wireless Parallel and Circulation Current Reduction of Droop-Controlled Inverters[J]. Transactions of China Electrotechnical Society,2018, 33(07): 1450-1460(in Chinese).
[21]Qing Liu, Tongyu Zhang. Adaptive droop control of DC distribution network considering photovoltaic output power margin[J]. Journal of physics. Conference series, 2021, 1871(1).
[22]Qiang F. U., Jie ZHANG, Meng-xiang WANG. Circulation suppression control method based on dynamic droop coefficient adjustment[C]., 2019:1229-1233.
[23]Busbieha Ahmed, Hamadi Abdelhamid, Ndtoungou Auguste,et al. Modified droop control to improve performances of two single-phase parallel inverters[C]., 2017:6470-6475.
[30]韩京清. 自抗扰控制技术[J]. 前沿科学,2007.
HAN Jingqing. Auto Disturbances Rejection Control Technique[J]. Frontier Science,2007,Chinese).