郑州大学护理健康学院
摘要: 本文指出了一般教材中关于一个重要极限的证明中存在的问题.讨论了该重要极限与圆的面积公式的等价关系.
关键词: 极限方法 重要极限 圆面积公式 等价关系
中图分类号 文献标志码
高等数学或数学分析课程中,都要在引入极限概念后讲述两个重要极限,其中之一是
 . (1)
. (1)
所以称它是”重要”极限, 是因为正弦函数的导数公式是由它推导出来的, 其意义不言自明.
在这里首先要指出该公式是不可以用洛必达法则证明的, 因为用洛必达法则要用到正弦函数的导数公式 ,而这个导数公式是由此重要公式推导出来的, 这构成了一个逻辑循环.
在公式(1) 的证明中要用到不等式
![]() (2)
(2)
在这个不等式的证明中大多数教材都用了扇形面积公式, 扇形面积公式又来自圆面积的公式. 在中小学课程里是用直观的方式描述了圆面积公式,![]() 被印到了学生的脑子里. 在承认圆的面积公式的前提下证明不等式(2)无可厚非, 但在逻辑上有点瑕疵, 因为毕竟没有把圆的面积公式说清楚. 如果按照后面用定积分来定义和计算圆的面积时,要计算积分
被印到了学生的脑子里. 在承认圆的面积公式的前提下证明不等式(2)无可厚非, 但在逻辑上有点瑕疵, 因为毕竟没有把圆的面积公式说清楚. 如果按照后面用定积分来定义和计算圆的面积时,要计算积分
. ![]() (3)
(3)
若用三角代换就要用到![]() 的导数公式,而
的导数公式,而![]() 的导数公式推导又要用到
的导数公式推导又要用到 ![]() 的结果,这又造成了逻辑循环。怎么解决这个问题呢?就以上分析可以从两方面入手, 一是不用圆的面积公式来证明不等式(2), 一是不用三角代换计算积分(3). 后者可以实现, 但计算(3) 毕竟离公式(1)的出现地太远了, 限于篇幅在此不再赘述.下面来实现第一个方案. 以下首先定义圆弧的长,
的结果,这又造成了逻辑循环。怎么解决这个问题呢?就以上分析可以从两方面入手, 一是不用圆的面积公式来证明不等式(2), 一是不用三角代换计算积分(3). 后者可以实现, 但计算(3) 毕竟离公式(1)的出现地太远了, 限于篇幅在此不再赘述.下面来实现第一个方案. 以下首先定义圆弧的长,
作者简介: 李映萱 (2005-- ) 河南项城县人 Email: lmr@zzu.edu
再用弧得到长与圆心角的关系证明不等式(2)
设在半径为![]() 的圆中有圆弧
的圆中有圆弧![]() ,其对应的圆心角为
,其对应的圆心角为![]() , 将圆弧分为
, 将圆弧分为![]() 等分,连接各分点得到一条折线, 它的每小段对应的圆心角为
等分,连接各分点得到一条折线, 它的每小段对应的圆心角为![]() , 每小段的长度为
, 每小段的长度为![]() , 折线总长为
, 折线总长为![]() . 易知
. 易知
![]() ,
,
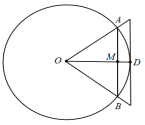 故{
故{![]() }是一个单增数列.
}是一个单增数列.
由于 ,
, ![]() .
.
于是
![]() ,
,
此表明{![]() } 有上界,从而{
} 有上界,从而{![]() }有极限, 记极限为C. 我们有理由把C 称为弧
}有极限, 记极限为C. 我们有理由把C 称为弧![]() 的长 (此定义与曲线长度的一般定义一致). 由此有
的长 (此定义与曲线长度的一般定义一致). 由此有
![]() . (4)
. (4)
如果承认了圆的周长公式,并引入角的弧度制,则有
![]()
故不等式(3)成立. 至此我们没有用圆面积公式证明了(3)式.
仔细推敲,这里还有一个圆的周长为什么是![]() 的问题, 从小学到大学还没有真正交待过, 而角的弧度制又与它相关,并且存在一个公式问题, 前述的那个C
的问题, 从小学到大学还没有真正交待过, 而角的弧度制又与它相关,并且存在一个公式问题, 前述的那个C
是否就是 ![]() .由于篇幅所限,以下只 按照上面得出C 的极限方法定义圆的周长和面积 ,并对公式进行一个解释. 最后揭示一个重要的事实.
.由于篇幅所限,以下只 按照上面得出C 的极限方法定义圆的周长和面积 ,并对公式进行一个解释. 最后揭示一个重要的事实.
设圆内接正![]() 多边形周长的数列为{
多边形周长的数列为{![]() }.
}.
根据三角形两边之和大于第三边的定理,该数列单调上升.同样的道理可
知相应的圆的外切正![]() 多边形周长的数列 {
多边形周长的数列 {![]() }单调下降
}单调下降
易证:对于任意正整数![]() ,
,![]() .
.
事实上,设OA是外切正多边形的边心距. OM是内接正多边形(边数和外切的
一样多)的边入心距. ![]() ,内接与外切的这两个多边形相似,它们的周长之比等于任意一对对应线段之比,所以
,内接与外切的这两个多边形相似,它们的周长之比等于任意一对对应线段之比,所以
![]()
因此![]() . 于是
. 于是
![]()
这表示{![]() }的一切项都小于
}的一切项都小于![]() ,
,![]() 是它的上界, 根据单调有界数列必有极限的
是它的上界, 根据单调有界数列必有极限的
定理,![]() 有极限,记为
有极限,记为![]() . 用同样的方法证明
. 用同样的方法证明![]() 有极限,记为L.
有极限,记为L.
最后来证明![]()
 其中
其中![]() 是圆周角.
是圆周角.
![]() 所以
所以![]() 我们有理由定义这极限
我们有理由定义这极限![]() 为圆周之长. 按照这个圆周长的定义,可以定义
为圆周之长. 按照这个圆周长的定义,可以定义![]() ,
,![]() 为圆的半径. 但是还要证明
为圆的半径. 但是还要证明![]() 是常数,与
是常数,与![]() 无关. 考察两个圆,设它们的半径分别为
无关. 考察两个圆,设它们的半径分别为![]() 和
和![]() ,周长分别为
,周长分别为![]() 和
和![]() . 对于它们如上做同样的处理,所得相同边数的内接正多边形的周长分别记为
. 对于它们如上做同样的处理,所得相同边数的内接正多边形的周长分别记为![]() 和
和![]() . 由位似多边形的性质,
. 由位似多边形的性质,![]() 和
和![]() 的比等于它们半径的比:
的比等于它们半径的比:
![]()
![]()
取极限得![]() ,按上述
,按上述![]() 的定义,代入
的定义,代入![]() ,得
,得![]() 或
或![]()
此表明![]() 是一个常数,与圆的半径无关. 于是有了圆的周长公式
是一个常数,与圆的半径无关. 于是有了圆的周长公式![]() .
.
类似的,可以定义圆的面积![]() ,并且可以得到
,并且可以得到![]()
事实上,只要把上述的内接和外切正多边形周长序列![]() 和
和![]() 分别改为相应的面积序列
分别改为相应的面积序列![]() 和
和![]() 即可证明后二者的极限存在并相等,从而可以定义该数为圆的面积. 又圆外切正多边形的面积与周长的比为
即可证明后二者的极限存在并相等,从而可以定义该数为圆的面积. 又圆外切正多边形的面积与周长的比为![]() ,故
,故![]() ,
, ![]()
如果事先如上定义圆的面积,再来证明公式(1)逻辑上就没有问题了. 反
过来, 如果承认公式(1),也可以按如上定义的圆面积得到圆面积公式
![]() 事实上,用
事实上,用![]() 表示内接多边形的边长,则
表示内接多边形的边长,则
![]()
![]() (5)
(5)
于是有如下结论:
重要极限(1)与圆面积公式(5)是等价的.
结束语
若承认圆的面积公式来证明不等式(2), 并无不可,逻辑上有点值得商榷.
本文用极限方法定义了圆弧的长度, 并由此避开了圆的面积公式证明 了不等式(2). 另外用极限方法定义了圆的面积并由此得到计算公式..这些定义是与一般曲线的长度的定义和一般图形的面积定义相一致的. 本文的目的并不在于只是从逻辑上完善重要极限的证明,而是强调极限方法, 极限方法是微积分的精髓,是联系无限与有限的桥梁. 圆的周长和面积都是无法用有限步的计算得到的量,而无限步的计算又无法实现, 极限方法可以合情的得到这些量的精确值. 对于圆的周长和面积,中小学课程中用描述的直观的做了解释, 到了大学应该给出一个合适的交待..
单就重要极限的证明,已有很多讨论,见仁见智. 有些书上把这个极限作为合情的假设. 有些书上,例如[2]和[3],明确指出可以证明:“对于光滑的曲线弧段,弧段与其对应弦长之比当弦长趋向于零时的极限等于1”,或换个说法,“对于光滑的曲线弧段当弦长趋向于零时弧段与其对应弦长是等价无穷小量”.如果事先明确指明这些事实,就可以不加证明地承认这个重要极限成立。这种处理也无不妥,反而是揭示了问题的本质:圆的弦长与其对应的弧长当圆心角趋向于0时是等价的无穷小量.微积分就是以可以局部"以直代曲"的问题为主要对象.
参考文献
[1] 王书彬 高等数学, 高等教育出版社,,2019
[2] 孙丽华、张魁元,工科数学基础,高等教育出版社,2004
[3] 马知恩、王绵森,高等数学简明教程,高等教育出版社,2009
Notes On Limitation ![]()
Li ying xuan
(School of Nursing Zhengzhou University)
Abstract: This paper points out the problems in the proof about an important limitation in Calculus books. Discusses the equivalent relation between this limitation and the formula of the area of
the circle.
Key worts: limitation method, important limitation, the formula of the area of the circle, equivalent relation.