深基坑临铁侧有限土体压力理论计算研究

深基坑临铁侧有限土体压力理论计算研究

李鑫,孙旻,滕延京,孙钧

中建八局第四建设有限公司 山东省青岛市 266000

摘要：本次研究主要通过国内外研究现状进行有限土体压力理论计算研究推导，计算项目邻近铁路侧、邻近建筑侧有限土体压力。

关键词：有限土体压力  极限平衡理论 

1、研究背景

项目位于上海市区，周边邻近铁路营业线及已建成房屋，基坑面积1.5万㎡，基坑开挖深度为10.8m，既有建筑物基础深度为3.5m，既有建筑距离基坑最近距离为10.6m，既有建筑物基础深度为1.2m，铁路营业线距离基坑最近距离为27.3m，建筑物集中恒荷载为40kN/m3，活荷载为4.0kN/m3，铁路营业性集中恒荷载为2.5kN/m3，活荷载为8.0kN/m3，土对墙背的摩擦角（墙背粗糙，与墙背几乎无滑移）δ=（0.67~1）ϕ，建筑物侧墙背摩擦角取26.67°，铁路营业性墙背摩擦角取23.33°。

   本次研究主要通过国内外研究现状进行有限土体压力理论计算研究推导，计算项目邻近铁路侧、邻近建筑侧有限土体压力。

2、国内外研究现状

有限/半无限土压力理论计算研究主要基于经典土压力理论发展而来，随着计算机应用的普及及应用，数值模拟技术逐渐成为土压力计算重要方法，通过引入高精度应变测量仪器，使试验数据与工程检测数据相结合，促进了土体压力研究。

2.1 朗肯和库伦土压力理论

经典朗肯土压力理论通过研究弹性半空间体内的应力状态，根据土的极限平衡条件而得出的土压力计算方法，库伦土压力理论根据研究挡土结构后滑动土楔体的静力平衡条件而得出的土压力计算理论。

两种理论提出依据、假设条件、实际应用情况存在差异。计算过程均假设挡土结构外侧土体处于极限平衡状态，推导结果为不同形式，朗肯土压力理论计算土压力强度分布形式与大小，库伦土压力理论假设分布形式为三角形计算挡土结构作用的土压力合力。

在实际工程中，由于它们能满足工程上所要求的精度，在许多工程领域中应用。由于朗肯理论忽略了实际挡土结构背并非光滑和存在摩擦力的事实，使计算得到的主动土压力偏大，而计算的被动土压力偏小。

大量的室内实验和现场观测资料表明,库仑理论计算的主动土压力大小与实测结果非常接近,但被动土压力与实测值则误差较大。因此，计算挡土结构后土体被动土压力时不采取库伦土压力计算理论。

朗肯土压力理论适用于挡土结构后的土体为水平的黏性或无黏性土，库伦土压力理论适用于填土表面为水平方向或有一定倾角的无黏性土，实际计算过程中通过图解法补充计算无黏性土的土压力。

2.2 半无限土体研究最新进展

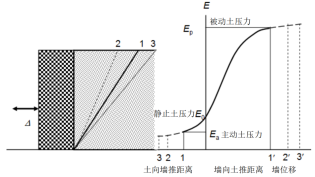
通过不同维度试验研究，推进半无限土体研究发展。经典土压力主要存在三个明显的缺点：一是假设土体变形完全达到极限状态的临界条件；二是没有考虑挡土结构的变位方式及其位移对土压力的影响；三是要求挡土结构为均匀平移。由于岩土工程的复杂性，挡土结构实际的变位模式和位移情况与经典土压力理论计算不符，土压力很难用采用理论精确计算，通过提高计算精度，研究得出刚性挡土结构土压力准确分布情况，是挡土结构设计重要经济因素。

通过岩土工程实验得到了土压力系数与挡土结构水平位移之间的关系，经过大量试验验证与理论推导，研究得出密实砂土达到主动极限状态时，挡土结构需要向坑内移动0.001H的距离，达到被动极限状态则需向坑外移动约0.05H。[1]

基于刚性挡土结构在平动模式下砂性土的土压力试验，利用黏性土在挡土结构平移、绕挡土结构底部转动和绕挡土结构顶部转动三种典型变位模式情况下进行试验研究，研究得出三种不同变位模式下刚性挡土结构土体土压力的强度大小与分布形式，绕挡土结构顶转动时强度曲线是上部土压力大而下部小的近似于抛物线的形状，而绕挡土结构底转动时则可以近似看作是三角形分布的形状。[2]

通过考虑挡土结构的变位模式以及位移量，土体抗剪强度和挡土结构土摩擦角、挡土结构各点处的位移量有关。通过建立了两者之间关系，简化主动土压力计算方法，研究得出不同位移模式，以及数值模拟的结果和试验结果均相互吻合。

以不同变位模式且考虑位移效应的刚性挡土墙为研究对象，将不同变位模式与考虑位移效应的挡土墙应用到水平薄层分析法中，对水平层分析法进行推广，利用水平层分析法推导研究得出挡土结构各种变位模式下的土压力分布公式。

墙体变位模式包括三种基本变位模式：平移(T)、绕墙底转动(RB)、绕墙顶转动(RT)。通过对T、RB和RT模式的主动和被动土压力分布进行详细推导，研究得到了相应形式下土压力的分布。

在研究任意深度的土力与该点挡土结构的距离的关系之外，同时考虑在土擦角和土体内摩擦角的影响下，借助土拱效应理论，研究在不同模式下刚性挡土结构后主动土压力分布形式与大小的问题，提出了计算主动土压力的理论方法。在刚性挡土结构平动位移模式下分别考虑外摩角和后填内摩角对挡土结构变形位移影响，建立了挡土结构土外摩擦角、土体内摩擦角与挡土结构位移之间的关系式。

2.3 有限土体压力研究现状

通过对两排刚性粗糙竖直挡土结构之间有限土体不同填土宽度下挡土结构上的土压力分布形式、大小规律进行研究。在计算围护结构上的主动土压力时,将挡土结构后的水平应力与平均垂直应力的比值作为侧土压力系数。

考虑挡土结构土之间的作用力以及墙后土体黏聚力,对是否考虑土体表面裂缝对土压力强度、分布形式影响进行分析研究。研究发现了有限土体土压力计算过程中,墙土之间作用力与挡土墙倾角、墙土摩擦角、滑裂角和土体内摩擦角等均有密切的关联。

依据土体的塑性理论,研究了压力分布形式以及有限土体主动土压力计算方法，并与经典土压力计算理论(朗肯土压力理论)进行对比分析,指出利用该公式计算的有限土体主动土压力与经典的朗肯土压力理论的计算结果存在比较明显的不同。

使用Plaxis有限元数值模拟软件对在稳定斜坡或有限体的挡土墙上的静止压力的分布规律进行了较深人的研究,分析结果与离心试验结果进行了对比,两者体现了较好的吻合。

采用极限状态几何力学平衡理论,在假定平面滑裂面的条件下,以数学与力学计算表达式的形式研究了有限土体土压力,并分析了有限土体滑裂角的变化规律以及影响因素。根据公式以及分析结果,表明有限土体滑裂角是受计算深度、有限土体宽度以及土体内摩擦角和土体黏聚力等因素影响,而不是经典的库伦土压力理论给出的定值。

对靠近既有建筑地下室的挡土墙,借助有限元数值模拟软件ABAQUS研究了刚性挡墙上的主动土压力问题，证明了滑裂角与土压力及宽高比有关,并给出了具体的墙后土体滑裂角以及有限土体主动土压力系数。

基于无黏性土和黏性土,研究了平动模式下在挡墙后土体不同宽高比,有限土体的被动滑裂面形状与倾角的分布影响规律。同时基于库伦平面滑动面,通过假定多道滑裂面,推导了被动土压力滑裂角及土压力强度大小与分布形式等被动土压力问题。

2.4 基坑开挖对附件既有建筑及设施稳定性影响研究现状

根据基坑沉降曲线的变化规律，对相邻建筑物的不同损伤形式进行了分析总结，最后得出控制相邻建筑物损坏的标准和防止相邻建筑物的控制措施。通过分析整理基坑现场检测数据，总结出基坑变形规律，同时得出了建筑物变形程度受其与基坑边缘距离的影响。

通过分析某基坑施工过程中临近建筑的明显不均匀沉降，结合了实际工程测量情况及该地区的土质分布等条件，综合分析探讨了建筑物产生较大整体沉降的原因。运用周围土层沉降计算法对某基坑周边建筑物进行理论计算。通过计算得出理论值和实际沉降的差异，并指出产生偏差的原因。

通过有限元模拟临近建筑桩基础弯矩和位移分布，并将其数据实际工程测量值进行对比，得到了基坑开挖时临近桩基础的变化规律，提出了桩基断裂判断方法，明确了桩的脆弱点同时总结出相应的加固措施和方案。分析引起地基不均匀沉降的本质因素并提出相应技术措施对其进行控制，同时分析不同沉降方式、有无差异沉降等不利因素的影响，得出最不利影响因素。

运用有限元软件FLAC4.0建立数值模型，分析基坑开挖过程中不同距离对支护结构变形的影响，得出在一定距离的范围内，建筑物倾斜值会随着开挖深度的增加而增大。以连续墙加锚杆支护类型为研究对象，利用软件模拟分析在建筑物距离基坑一定范围时，锚杆层数变化对周边建筑物的变形影响，总结出锚杆水平间距优化的新方法。

通过分析地面沉降简化计算模式下的基坑开挖对临近建筑物的影响，并认为该方式计算结果接近考虑共同左右下的有限元结果，验证其可行性。王震宇利用弹塑性本构模型，对比分析了数值模拟结果与实测值，得出弹塑性本构模型的计算结果更贴近实际情况。

通过有限元模拟分析，得出了基坑和邻近建筑之间的相互作用，以及基坑与邻近建筑物之间存在的内在联系。采用HHS土体本构对不同间距的基坑建立有限远模型，同时考虑固渗耦合，分析不同间距对基坑支护桩位移和弯矩的影响。分析不同因素下的基坑变形情况并通过关联基础变形和上部结构安全状态的关系，得出定量分析结果。

目前有限土体土压力计算已不能继续使用经典土压力理论进行计算分析与设计，考虑土体黏聚力的影响，认为有限土体承受主动土压力时，其滑裂线仍可以认为是直线，考虑了既有建筑基础与有限体之间的相互作用力，推导成立了计算有限土体主动土压力的公式。

在有紧邻建筑的拟建基坑开挖过程中，会出现三类情况中的一种或两种，甚至会在同一个基坑开挖过程中同时出现三种情况，因此三类情况也可以理解为开挖过程中的三个阶段。

第一类情况，当基坑开挖深度在一定深度之内时，滑裂线未与紧邻建筑相交，虽然会受到既有建筑的影响，但影响很小，此时可以近似按半无限土体计算。

第二类情况，当基坑开挖达到一定深度，滑裂线与紧邻建筑打的地下室外墙或围护结构相交，此时为有限士体比较典型的情况。

第三类情况，此时基坑开挖到一定深度，滑裂线与既有建筑底板相交，情况特殊，推导得出土体滑裂角与不同因素关系式，滑裂角非定值，为与土体宽度、密度、内摩擦角等因素相关的系数。

3、粘性土主动土压力理论计算

3.1 相关研究方法

已有一些学者对于有限土压力进行研究，但多是在大量的假设的基础上得出相应的计算方法理论。

马平等基于极限平衡理论及平面滑裂面假定，考虑土体粘聚力，通过直接建立有限土体的静力平衡方程求出挡土墙上的土压力的表达式,得到相应的剪切破坏角及对应的土压力，运用极限状态建立有限土体计算模型，推导了有限土体滑裂面剪切破坏角的数学表达式，建立了有限土体主动土压力的计算公式，通过对有限土体状态下支护结构背部的梯形土体进行整体受力分析，推导出土压力合力E的表达式，认为E为θ的函数，对其求导，此时 E 取极值 E即为主动土压力合力，进而求得产生主动土压力时的剪切破坏角θ'值。若，支护桩 (墙) 后土体处于有限土体状态此时先计算剪切破坏角，然后计算总土压力，再采用差分形式进行主动土压力强度计算。[3]得到了有限土体土压力结果明显小于经典土压力结果，且有限土体土压力强度与开挖深度呈非线性关系，同时得到了以下公式：

式中:  

z--计算点的深度，m;

γ--土体重度，kN/m³，即有限土体宽度;

θ--滑裂角，即滑动破坏面与水平面的夹角，(°);

b-既有构筑物距拟建基坑的距离，m;

高印立基于土的塑性上限理论，按照相关联流动法则，推导出了有限土体主动及被动土压力强度的表达式：

式中:

，主动土压力系数；

>1时，取=1； 为有限土体主动土压力强度 (kPa)；

式中:

，被动土压力系数；

>1时，取=1；为有限土体主动土压力强度 (kPa)。

3.2规范建议方法

对有限土体，有些城市出台了相关的规定，地区规范对于有限土体的情况进行了如下的规定,该方法是以摩尔库伦破坏准则为基础发展起来的,按照此类方法的设想，当挡墙外的土体达到极限破坏状态时,大小主应力存在以下关系:

由于邻近建筑物基础的存在,使得有限土体土压力在计算过程中,滑裂面被既有建筑物的基础所截断。因此通过引人参数而来近似体现滑裂面被截断的影响。

由于滑移土体部分的重量减小至初始的倍,滑移线的长度也变为初始的加倍,故得出了规范中的公式。

当基坑的邻近建筑物的基础在基坑底面以下，并且外墙到支护结构的净距b小于时,采用以下方法计算土体的土压力:

1）计算深度或时，按照朗肯土压力理论计算。

2）计算深度时：

①黏性土、粉土以及碎石土和砂土时，土压力强度P采用以下方法计算：

；

②碎石土和砂土位于地下水位以下时，土压力强度P采用以下方法计算：

；

其中：

H--基坑深度，m;

    --邻近建筑物的基础埋深，m;

Z--计算点深度，m;

--系数，；

本计算方法未考虑既有构筑物基础对有限土体影响，假设滑裂角即滑移线与竖直面的夹角为，为近似取值法。

3.3 粘性土主动土压力理论计算

通过对挡土墙与既有建筑基础间的有限土体进行完整的受力分析，考虑既有建筑基础与有限土体间的法向及切向的相互作用力，建立了求解关于有限土体主动土压力的计算方程,推导出了有限土体主动土压力的计算公式,并进行了适当的简化。

通过比较分析并结合前期相关研究,发现两侧墙体上的土压力存在一定的数量关系,为计算有限土体两侧建筑墙体传递的压力 N、E 的数值关系，做以下近似假定:

1）假定作用在支护构件上的土压力沿墙高呈三角形分布；

2）假定两侧墙体在同深度处对有限土体作用力压强相同；

3）土体黏聚力 c 在一定深度范围内压力为零，计算公式同朗肯土压力。

通过以上的分析，N、E的大小关系可以通过上图的几何关系表示出来，有限土体达到主动状态时的受力情况所示。挡土构件与已有建筑基础的距离为b,挡土构件高度为H滑裂面与水平面夹角为θ，墙土摩擦角分别为δ1、δ2，土体黏聚力为c，土与墙体之间黏聚力分别为C1’、C2’，挡土构件作用于有限土体的水平力大小为E，有基础作用于有限土体的水平力大小为N，滑移土体重量为W,从图中几何关系可以求出土重W的表达式为:

考虑上部土体与墙背脱离，切向力扣减H’=H-Z0,，h’=h-Z0，根据朗肯理论计算，c、ϕ是土体强度参数，墙土界面的强度参数由相邻土体强度参数折减得出，折减后的黏聚力和内摩擦角分别为C、δ。由库伦强度理论可知两侧墙体施加给有限土体的切向力大小分别为Etanδ1+C1’H’和Ntanδ2+C2’h’。底部滑裂面处的正应力与剪应力存在相同的关系，只是强度参数为C、ϕ，在计算黏性土的土压力时，不仅应考虑滑裂面存在的黏聚力C以及墙土间的摩擦角δ，而且还应考虑墙土间的黏着力C1’，墙土间存在黏着力，这一点已经为一些工程的拔桩试验所证实。黏着力大小主要与填土的黏聚力有关,根据莫热菲基洛夫的研究，认为黏着力C’可采用，其中：。

根据力平衡条件建立两个平衡方程，求解N、E、R未知数。

引入参数：

建立平衡方程：

求解:

    根据土压力极值条件建立方程，求解θ未知数。

；

通过近似极限条件，计算土体滑动时土体与水平面夹角，令土体压力极限角度近似等于

。实际情况下，滑裂角θ并不是固定的，与计算深度、土内摩擦角、土粘聚力及有限土体宽度有密切关系，通过结合土体参数求解方程，计算滑裂角。[4]

4、有限土体压力理论计算

1）铁路侧有限土体压力理论计算：

主动土压力

朗肯理论计算：

参数计算：

土体压力极限角度近似等于：，m=-6.592;

求解得：E=-781.078KN;

2）建筑侧有限土体压力理论计算：

主动土压力：

朗肯理论计算：

参数计算：

土体压力极限角度近似等于：，m=9.036;

求解得：E=-320.527KN;

5、总结

通过对前人研究进行梳理分析，通过极限平衡法对基坑支护构件与既有基础(地下室)之间的有限土体进行受力分析，对项目实际有限土体压力进行理论实际计算，在考虑了既有建筑对有限土体作用力的情况下，建立相应的极限平衡方程，推导及计算有限土体土压力计算简化公式。

[1]K.Terzaghi,Large retaining wall tests. Ⅱ-pressure of dry sand[J]. Eng.News Record,1934,vol

[2]周应英，任美龙。刚性挡土墙主动土压力的试验研究[J].岩土工程学报，1990（02）：19-26.

[3]马平，秦四清，钱海涛.有限土体主动土压力计算[J].岩土力学与工程学报，2008（S1）;3070-3074.

[4]赵伯明，杨清源，王子珺，刘树亚.城市狭窄空间地下结构施工影响与控制。同济大学出版社，2018.8：224-238.