宣汉陈家咀码头对后河行洪的影响分析

宣汉陈家咀码头对后河行洪的影响分析

岑杰

机械工业第六设计研究院有限公司重庆院，重庆，401120

摘要：码头的修建势必对天然河流河道行洪造成一定的影响，本文以宣汉陈家咀码头为研究对象，建立二维数学模型，以P=10%的洪水流量作为计算工况，分析对后河工程河段行洪的影响。模拟结果表明，码头建设引起的过水面积最大缩窄率为0.01%，引起的最大壅水高度为0.05m，壅水影响局限在码头上游约 101m局部范围内，陈家咀码头不会对后河河道行洪产生不利影响；工程河段流速变化值在-0.05m/s~0.15m/s 之间，流速变化局限在码头上边界上游约63m，下边界下游约108m，说明码头修建前后流速影响有限。

关键词:行洪安全；内河码头；二维水流数学模型；影响分析；后河；河道行洪能力

0 前言

河流中修建码头会占据河道一定的过水面积，改变了工程河段河流状况，水流受到码头压缩，工程上游形成壅水，天然水面升高，对防洪可能产生影响；同时工程附近流场也会发生改变，加剧河床和岸坡的冲刷，影响河势稳定。因此为保障后河河道防洪安全，分析研究陈家咀码头对后河河道行洪能力影响是很有必要的。目前对于河道行洪能力分析方法主要有水文学、水力学方法，其中水力学方法[1]可以通过建立一维、二维水动力学模型分析不同频率和不同工况条件下河道行洪能力，是学者们普遍采取的一种方法。

李欣（2018）[2]采用曼宁公式法、能量方程法对小凌河河道行洪能力复核分析，认为复核的各河段行洪能力及对应的防洪标准与实际基本相符。王涛（2019）[3]等，采用了物理模型试验、数值模拟和经验公式方法分别模拟研究宽浅型河道糙率和桥墩壅水对行洪能力的影响，认为二维数学模型比经验公式和一维数学模型能较真实地反映行洪影响。金子嵩(2021)[4]基于MIKE21的二维潮流模型、SWAN波浪模型，研究港区建设对入海河流河道水力特性及行洪安全的影响。王玲玲（2021）[5]等，基于MIKE21 FM 建立工程区段二维水动力模型，采用 Moghadam 淹没植被明渠糙率公式模拟植被阻水作用，分析长江浦口段江滩复绿工程对河道行洪的影响。赖国友（2023）[6]等,构建了鉴江干流一维恒定水动力数学模型，计算洪水水位和流速变化对比分析采砂前后对行洪的影响。

因此，本文以达州市后河宣汉县河段陈家咀段为研究河段，采用资料整理、水文和水利计算分析以及工程附近二维水流数学模型相结合的方法，定量分析现状码头对河道行洪能力的影响。

1.河道概况

陈家咀码头位于后河宣汉县段左岸。后河是州河三大主要支流之一，为州河主要水源，发源于大巴山南麓(距万源45km)之大横山，海拔高程1480m，全长 154km，控制集水面积3634km2，河道平均坡降7.68‰。整个后河流域呈北高南低之势，由北向南西方向流动。后河上游地处大巴山暴雨区，流域上游为深山区，植被较好，两岸山高坡陡，相对高差在500～1000m以上，分水岭地带的海拔高程在2000m左右，中下游人类活动频繁，植被较差，水土流失严重，河道多沙洲漫滩，冲淤现象较重。工程河段为典型山区性河道，河谷切割较深，河床断面为不对称“U”型或“V” 型断面。受两岸地形控制，河道岸线规则，两岸岸坡较陡，全年河宽变化不大，河宽约120m~270m。

2 数学模型

2.1二维水流数学模型

；

；

。

上述三式中：u，v分别为x、y方向的流速分量； 为水深；g为重力加速度;t为动量方程的水平扩散系数（紊动粘性系数）；Sf ,x、Sf,y分别为x、y方向的河床阻力，可表示如下:

式中，n 为糙率系数。

2.2 计算区域以及网格的布置

根据工程河段所处河势条件以及工程河段实测1：2000江床地形图资料，并考虑计算需要进出口留有足够的长度，以便平稳地处理进、出口边界。模型选取的计算区域为：全长约2km，其中码头以上河段长1km、码头以下河段长 1km。进口边界采用流量控制，出口边界则由水位控制。在网格划分中，采用三角形网格离散计算区域，网格大小疏密沿河道河势宽窄变化不等。为提高模拟精度，报告对码头以上100m至码头以下100m范围内河段（共计200m长）进行网格的局部加密处理，最小网格间距为5m。

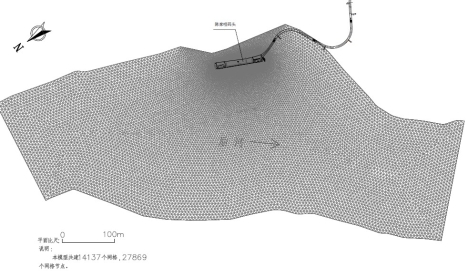
图1 数学模型计算网格

3 计算成果及分析

 3.1 壅水计算分析

由于陈家咀码头占据了一定的河道过水断面，从而导致工程河段水位发生改变。通常上游水位将有一定程度的壅高。本文最大壅水高度和壅水影响范围采用平面二维数模演算，各计算组合的最大壅水高度及其影响范围的计算结果见表1。

表1 工程河段最大壅水高度及影响范围

分析结果表明，尽管码头的存在会产生一定的壅水，但其壅水仅局限在码头附近范围，具有局部性质，说明码头的建设对河道的影响具有明显的局部性。

3.2 流速计算分析

为了研究码头的建设对工程河段航道条件的影响，采用二维数学模型分析了码头工程建设前后工程河段的航道条件及其变化。本文采用二维水流数学模型对码头建成前后各工况工程河段的流场进行了计算，本文取最大流量Q10%=6417m3/s时为计算流量。

图2 工程前工程河段流场图（Q=6417m3/s）

图3 工程前工程河段流场图（Q=6417m3/s）

根据计算结果表明，在P=10%洪水条件下，工程后码头上游局部区域流速有所减小，码头下游局部区域流速略有增大，其中：码头上游局部区域流速减小最大值为0.05m/s，码头下游局部区域流速增大最大值为0.15m/s。流速变化局限在码头上边界上游约63m，码头下边界下游约108m 范围内。

根据前面分析，码头在P=10%洪水工况下占据的最大过水面积仅0.01%，因此其阻水作用很小。从码头修建前后的流速等值线分布来看，在P=10%工况下洪水码头上游流速变幅为-0.05m/s～0m/s，码头下游流速变幅为0m/s～0.15m/s，流速变化幅度较小，不会引起河道发生大的冲淤变化。而码头前沿结构型式为直立挡墙，结构稳定，抗冲能力强。由此可见，工程建设后引起的挟沙力改变也局限在工程附近较小的范围内，产生的泥沙淤积和冲刷范围有限，加之工程河段河床组成较为坚硬，抗冲能力较强，基本不存在产生大范围强烈的普遍冲刷和淤积等河势改变的水动力条件和河床边界条件。综上所述，工程后不会导致附近水域的滩槽和河道岸线、平面流速及动力轴线发生大的变化，码头对所在河道的河势稳定影响较小。

4 总结

（1）结合二维数学模型分析，当遇P=10%洪水时，码头建设引起的过水面积最大缩窄率为0.01%，引起的最大壅水高度为0.05m，壅水影响局限在码头上游约101m局部范围内，因此，码头的建设不会对河道行洪产生不利影响。

（2）当遇P=10%洪水时，码头修建后，工程河段流速变化值在-0.05m/s~0.15m/s之间，流速变化局限在码头上边界上游约63m，下边界下游约108m，说明工程修建前后流速影响有限。由于本河段边界抗冲性较强，流速小幅度的改变不会引起后河工程河段河势发生明显的变化。

（3）码头不会对后河工程河段的防洪水位和河道泄洪产生明显不利影响，不会改变现有岸线状况，对河势条件和河床演变影响很小。

参考文献

[1]尹雄锐,胡春媛,王晓妮.嫩江河道围堤对行洪能力的影响分析[J].水电能源学,2022,40(10):78-81.

[2]李欣.河道行洪能力复核分析与计算[J].水土保持应用技术,2018,182(02):28-30.

[3]王涛,郭新蕾,李甲振等.河道糙率和桥墩壅水对宽浅河道行洪能力影响的研究[J].水利学报,2019,50(02):175-183.

[4]金子嵩.浅析港区对河流水力特性及行洪安全的影响[J].江西水利科技,2021,47(04):242-249.

[5]王玲玲,姜兆宇,韩建军等.长江浦口段江滩复绿对河道行洪能力的影响[J].河海大学学报(自然科学版),2021,49(04):316-321.

[6]赖国友,田甜,程香菊.鉴江采砂对行洪的数值模拟及影响分析[J].水利规划与设计,2023,234(04):38-41.