水箱液位控制PID的MATLAB参数整定及仿真

水箱液位控制PID的MATLAB参数整定及仿真

高金龙

（华北电力试验研究院，天津市河东区，300012）

摘要：PID控制器主要针对控制对象来进行参数调节。PID的归一参数整定法和试凑法费时，费力。针对这一问题，探讨MATLAB实现PID参数整定及仿真，同时观察控制参数对PID控制规律的影响。

关键词：PID；参数整定；仿真

1 引言

PID控制器又称为PID调节器，是按偏差的比例P、积分I、微分D进行控制的调节器的简称，它主要针对控制对象来进行参数调节。因为它算法简单、稳定性好、工作可靠、鲁棒性好，在工程上易于实现，但PID控制器的参数整定方法复杂，通常采用PID归一参数法和试凑法来确定，但较费时、费力。针对这一问题，文中探讨用MATLAB实现PID参数整定及仿真的方法及控制参数对PID控制规律的影响。利用MATLAB强大的计算仿真能力，解决了利用试凑法来整定参数浩繁的工作，可以方便、快速地找到使系统达到满意性能指标的参数。

2 PID控制器的原理与算法

图1是典型PID控制系统结构图。在PID调节器作用下，对误差信号分别进行比例、积分、微分控制。

PID控制算法的模拟表达式为

μ (t) =Kp [ + +Td de(t) dt ]

相应的传递函数为：Gc(s)= Kp(1 +S + TdS)

3 水箱水位调节系统：一个典型的水箱水位自动控制系统如下图所示。

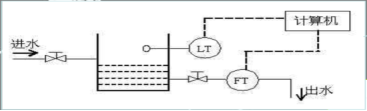
这个水位控制系统中，水池的进水量Q1来自手动控制开度的进水阀门，通过调节出水阀门调节出水量Q2，使水箱水位保持设定水位不变。这个系统是个典型单冲量自动调节系统，在该系统中：

系统中各组成单元的模型如下：

水箱对象模型：G(s)= 液位传感器：量程0~40cm

执行阀：对应0~100%开度

系统的方框图如图所示：

4 PID控制器的MATLAB仿真

PID控制器的参数Kp、Ti、Td分别对系统性能产生不同的影响。在控制过程中如何把Kp、Ti、Td 3参数调节到最佳状态，需要深入了解PID控制中3参数对系统动态性能的影响。下面讨论水箱水位调节系统中当一个参量发生变化，对应曲线的实时变化。

4.1 P控制作用分析

根据模型中的传递函数，给出初始积分时间Ki值为0.1，当P比例作用值依次为6、5、4、3、2、1时，对应的曲线变化。为了找出最佳的P值，采用了下列MATLAB仿真程序：

close all PID=[65,0.1,0;    55,0.1,0;    45,0.1,0;    35,0.1,0;    25,0.1,0;    15,0.1,0];%初始化PID参数

for pid=1:1:6  ts=0.005;  %采样时间=0.05s

sys=tf(20,[200,1]);   %建立被控对象传递函数，即传递函数

dsys=c2d(sys,ts,'z');      %离散化

[num,den]=tfdata(dsys,'v');  e_1=0;      %前一时刻的偏差     

Ee=0;       %累积偏差

u_1=0.0;    %前一时刻的控制量

y_1=0;       %前一时刻的输出

kp=PID(pid,1); ki=PID(pid,2); kd=PID(pid,3);

u=zeros(1,2000); time=zeros(1,2000);

for k=1:1:2000

    time(k)=k*ts;   %时间参数

    r(k)=500;      %给定量

    y(k)=-1*den(2)*y_1+num(2)*u_1+num(1)*u(k);

    e(k)=r(k)-y(k);   %偏差

    u(k)=kp*e(k)+ki*Ee+kd*(e(k)-e_1);  

    Ee=Ee+e(k);  u_1=u(k); y_1=y(k); e_1=e(k); end

subplot(2,3,pid);

p1=plot(time,r,'-.');xlim([0,10]);hold on;

p2=plot(time,y,'--');xlim([0,10]);

title(['Kp=',num2str(kp),' Ki=',num2str(ki),' Kd= ',num2str(kd)]);

hold on;end

结果下图所示

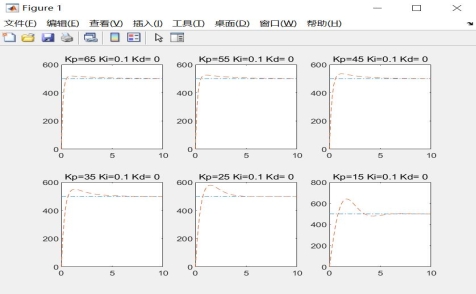
由上图可知Kp值为65时，调节效果最佳。

3.2 比例积分控制作用的分析

Kp值确定为65时，调节Ki的值依次为0.5、0.4、0.3、0.2、0.1时，观察曲线查看Ki值对PID调节的影响。程序如下：

   close all PID=[65,0.5,0;    65,0.4,0;    65,0.3,0;    65,0.2,0;    65,0.1,0;    65,0,0];%初始化PID参数

for pid=1:1:6 ts=0.005;  %采样时间=0.05s

sys=tf(20,[200,1]);   %建立被控对象传递函数，即传递函数

dsys=c2d(sys,ts,'z');      %离散化

[num,den]=tfdata(dsys,'v');  e_1=0;      %前一时刻的偏差     

Ee=0;       %累积偏差

u_1=0.0;    %前一时刻的控制量

y_1=0;       %前一时刻的输出

kp=PID(pid,1); ki=PID(pid,2); kd=PID(pid,3);

u=zeros(1,2000); time=zeros(1,2000);

for k=1:1:2000

    time(k)=k*ts;   %时间参数

    r(k)=500;      %给定量

    y(k)=-1*den(2)*y_1+num(2)*u_1+num(1)*u(k);

    e(k)=r(k)-y(k);   %偏差

    u(k)=kp*e(k)+ki*Ee+kd*(e(k)-e_1);  

    Ee=Ee+e(k); u_1=u(k); y_1=y(k); e_1=e(k); end

subplot(2,3,pid);

p1=plot(time,r,'-.');xlim([0,10]);hold on;

p2=plot(time,y,'--');xlim([0,10]);

title(['Kp=',num2str(kp),' Ki=',num2str(ki),' Kd= ',num2str(kd)]);

hold on;end

由运行该程序后系统的响应曲线可知,为了改善系统的动态性能,如减小超调量,缩短调节时间,水箱液位调节系统中 PID控制器的参数 Ti应选用 0.1。

结语：

1，利用MATLAB对PID参数进行整定和仿真，省去了传统方法反复修改参数，反复试运行，方便、快捷、省时、直观。

2，增大比例系数Kp将加快系统的响应，有利于减小静差，但是过大会使系统有较大的超调，使稳定性变坏；Kp取值过小，会使系统的动作缓慢。

3，增大积分时间Ti有利于减小超调，减小振荡，使系统的稳定性增加，但系统静差消除时间变长；若过小，系统的稳定误差将难以消除，导致系统不稳定。

参考文献：[ 1]　张圣勤. MATLAB7.0实用教程，机械工业出版社，2009-1.

[ 2]　 薛定宇. 控制系统计算机辅助分析—Matlab语言及其应用[M]. 北京: 清华大学出版社, 1996.

[ 3]　王建国，孙灵芳，张利辉 电厂热工过程自动控制，中国电力出版社，2009-8.