装配式框格梁边坡防护之稳定性分析评价

装配式框格梁边坡防护之稳定性分析评价

杨树坡1 ,周兴1 ,任永强1  ,魏浩2, ,徐振源2

1.贵州中交玉石高速发展有限公司;  2.中交路桥建设有限公司 ）

摘要：本文以某高速公路高边坡装配式框格梁坡面防护工作为背景，详细的分析了装配式框格梁边坡防护稳定性，通过对不同边坡高度、岩土参数以及防护支护参数的选择；为装配式坡面防护技术提供安全与质量保障。

关键词：边坡工程 装配式 框格梁 预制构件 稳定性分析

目前高速公路高边坡常见的锚固技术锚杆、锚索框格梁防护技术，一般是采用现浇钢筋混凝土框格梁的施工工艺，但是由于施工时需搭设支架和模板，工期长，受气候因素影响大，费工费料，安全风险点多。越来越多的工程考虑采用装配式框格梁防护技术。

本文以某高速公路高边坡装配式框格防护项目为依托，通过研究不同的边坡尺寸、岩土参数及支护参数对装配式框格坡面防护稳定性的影响，为装配式框格梁边坡防护技术提供重要的支撑与参照。

1工程概况

项目区域沿线地形地貌较为复杂，主要以冲积平原、丘陵、山岭重丘区等为主，该高边坡挖方最大高度为26.8m。山坡自然坡度为15～30度，山上植被发育，山下为丘陵间沟谷，沟谷开阔，走向与线位近平行。地层揭露如下：

黏土层（Q4el+dl）：褐黄色，少量灰褐色，可塑，切面稍有光泽，无摇振反应，韧性、干强度中等。该层层厚1.40～1.50m。

强风化砂质白云岩：灰白色，隐晶质结构，层状构造，主要矿物成分为白云石，混少量方解石、黏土矿物等杂质，组织结构基本被破坏，矿物成分显著变化，岩石多风化呈碎块状和砂土状。

中风化砂质白云岩：灰白色，隐晶质结构，层状构造，主要矿物成分为白云石，混少量方解石、黏土矿物等杂质，裂隙发育，沿裂隙面铁锰质浸染，岩石破碎，岩芯多呈碎块状。该层未揭穿，本次钻探最大揭露厚度19.10m。

2 稳定性分析

2.1 模型建立

此次计算软件选用理正岩土，进行二维平面分析，坡面段为6段，施工图设计为：第一级坡率：1:0.75，10m高，第二级坡率：1:1,10m高，第三级坡率：1:1.25,6.8m高，其中第一、二、三级边坡之间设2m平台，坡顶向后取25m宽度，为了控制变量，本次主要研究第一、二级边坡，第三级边坡按1:1.25坡率执行。具体简图如下：

2.2 岩土参数选择

本次设计主要考虑三种材料，分别为：黏土、白云岩、锚杆，主要考虑重度、弹性模量、泊松比、粘聚力、摩擦角，5个物理力学参数，具体详见下表（其中锚杆重度为：钢筋与M30水泥砂浆的综合重度）：

表1：材料参数一览表

2.3 不同参数对装配式边坡防护稳定性影响

2.3.1 坡率

此次研究，分别对坡率为1:0.5、1:0.75、1:1、1:1.5的四组（均为第一、二级边坡）进行了计算，为了控制变量，两级坡率均设为一致，且均未设置任何防护方案，第三级边坡按1:1.25控制。计算结果如下表所示：

表2：边坡坡率—安全系数关系表

图1：坡率-安全系数关系图

通过分析可以看出，坡率在1:1之前，边坡安全系数与边坡边坡坡率之间存在线性关系，在1:1坡率之后，安全系数增加趋势更大，1:1.5时，安全系数已达到1.323，为避免大开大挖，同时保证边坡的安全可靠，本次设计坡率选取在1:1附近。

故此次设计考虑第一级边坡坡率选取1:1，第二级坡率选取1:0.75。通过计算，该方案的边坡安全系数为1.17，其值介于坡率分别为1:0.75和1:1的安全系数之间的合理区间范围。

2.3.2白云岩参数C、φ值

此次土体参数分析，主要是对白云岩的C、φ值分别进行了10%、20%、30%三种情况，共计7种工况（均为无防护情况下），得出的结果如下所示：

表3：C、φ值—边坡安全系数关系表

图2 C值—安全系数关系图

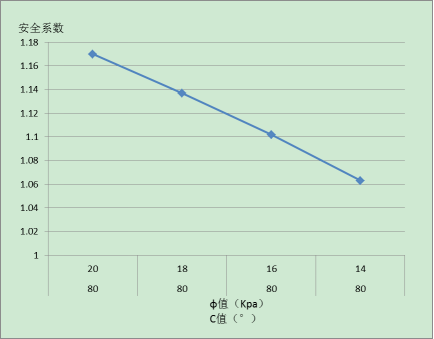
图3：φ值—边坡安全系数关系图

通过分析，总体上可以看出：（1）边坡安全系数随着白云岩C、φ值的折减，均呈现下降趋势，且近乎满足线性递减关系；（2）折减相同比例的前提下，C值对边坡安全系数的影响要大于φ值对边坡安全系数的影响，基本满足土力学中土的抗剪强度公式：τ=θtanφ+C。

故在边坡问题中，岩土体参数对边坡稳定有着重要影响，在天气等不利因素影响下，应尽量保证岩土体参数不弱化，若无法避免弱化，也亦优先保证岩土体的

C值不受影响，这就显得尤为重要！

2.3.3锚杆长度

本次工点设计采用的是钻孔直径90mm，锚杆直径32mm的全长粘结型锚杆，锚杆与水平面的夹角为20°。根据《岩土锚杆与喷射混凝土支护工程技术规范》（GB 50086-2015）中5.3.5点的要求，普通水泥砂浆锚杆的长度一般为1.5m～12m。

故此次研究选取长度分别为：6m、8m、10m、12m、14m，共计5组工况。计算所得结果如下所示：

表4：锚杆长度—边坡安全系数关系表

图4：锚杆长度—边坡安全系数关系图

通过以上数据分析，可以看出：随着锚杆长度的增加，边坡稳定系数逐步提高，且在锚杆长度12m之前，锚杆长度对于边坡安全的影响较大，在10m～12m之间的增量尤为明显；锚杆长度增加至12m继续增加后，边坡安全系数增长率速率放缓影响，且锚杆长度在12m时，安全系数已达到规范要求，若再进一步增加锚杆长度，意义不大。

2.3.4锚杆角度

在全长粘结型锚杆加固边坡的作用机理中，很重要的一点是，利用锚杆的抗剪作用阻止局部不稳定块体的滑落，锚杆作用形成开挖面的受力环区并将开挖面的高应力延伸到边坡面深处，改善“岩石混凝土结构体系”的承重效果，起到锁定岩石共同受力的作用，锚杆的这种作用效果类似于悬臂梁结构。这就显的锚杆的设计角度就显的尤为重要，如何实现锚杆体对边坡最经济最有效的防护效果是此次研究的目的。

此次锚杆角度研究，分别进行了0°、10°、20°、30°，共计4种情况下的安全稳定分析，计算结果如下所示：

表5：锚杆角度—边坡安全系数关系表

图5：锚杆角度—边坡安全系数关系图

从图5中可以看出，锚杆入射角在20°之前，随着入射角度的增大，边坡安全系数增大速率较大，增加20°后，随着锚杆入射角的进一步增大，安全系数增加不明显，基本可以判断出：当入射角＜20°时，锚杆可能并未完全贯穿滑动面；当入射角≥20°时，锚杆已完全贯穿滑动面。故此次设计中锚杆入射角度选定为20°。

2.3.5锚杆的粘结长度

非预应力锚杆的粘结长度是决定锚杆抗拔力的重要控制性参数，本次研究选取了粘结长度分别为0m、4m、8m、12m，合计四种情形，计算了各粘结长度下的受力情况。所得计算结果如下所示：

表6：锚杆粘结长度—边坡安全系数关系表

由计算结果可以看出，在同一计算模型中，当粘结长度大于4m以后（4m的粘结长度提供的抗滑力＞边坡下滑体的切向下滑力），粘结长度的增加对边坡的稳定及锚杆的受力情况不产生进一步的影响。

根据《岩土锚杆与喷射混凝土支护工程技术规范》（GB 50086-2015）中5.1.4点的要求：“非预应力锚杆杆体应全长用注浆料固结，应采取措施保证注浆饱满密实。”，对于多出部分的粘结长度可按安全储备进行考虑；同时，考虑施工单位在施工过程中的便捷性，使用全长粘结型锚杆，可谓是花了小的代价，获得了大的回报，达到了“事半功倍”的效果。

故此次设计按全长粘结型锚杆考虑，较为合理。

2.3.6锚杆的水平间距

此次研究选取了：“锚杆的水平间距”，这一参数对边坡的影响，分别进行了1m、2m、3m、4m、5m，共计5种情况下的计算。得到的计算结果如下所示：

表7：锚杆水平间距—边坡安全系数关系表

图6：锚杆水平间距—安全系数关系图

图7：锚杆水平间距—抗滑力关系图

通过图6、图7可以看出：（1）随着锚杆水平间距的增加，边坡安全系数呈现逐步递减的规律，且递减速率先快后慢，大约在水平间距为2m位置处为速率变化的拐点；（2）筋条上的抗滑力的变化规律呈现逐步递减的规律，且递减速率先快后慢：1m～3m时，逐渐递减，速率较大； 3m～5m时，逐渐递减，递减速率较小，水平间距在3m时，为该阶段的突变拐点，大致原因分析如下：当锚杆水平间距在0~3m范围时，岩土体产生了较为明显的“土拱效应”，增大了整体的抗滑移能力；当水平间距＞3m后，“土拱效应”明显减弱，故而出现了此次突变。因此本次设计所选的水平锚杆间距为3m，在合理利用岩土体自身材料特性的前提下，无需提高锚杆布设密度，达到了较为理想的支护效果。

2.4工程项目稳定性分析

通过以上最优参数的研究，拟通过运用

Midas GTS NX软件，在选用以上“最优”的参数后，进行边坡稳定性验证性计算。

2.4.1 模型建立

本次研究采用Midas/GTS进行辅助验证性计算，边界约束为：坡面顶面及坡面（右侧）为自由面，前后面限制y方向位移，底面与左侧面为固定端约束，同时，沿y轴扩展20m，最终形成三维实体，具体横断面尺寸详见下图（图中数据单位均以m计）：

图8：模型横断面图

图9：模型实体图

2.4.2参数选取

同2.2节，故此不再赘述。

2.4.3边坡失稳状态判别标准

当土体受力时，其内部的土颗粒受到挤压，移动，有的土颗粒甚至破坏并重新组合。土体的破坏是一个逐渐的过程，在破坏初期，某一部分土局部出现塑性应变区域，随着土体受力的增加或持续，塑性应变区域慢慢扩展，直到贯通整个边坡。在本次研究中，判断边坡是否破坏采用的是有限元数值计算不收敛时的安全系数以及结合塑性区的贯通程度。

2.4.4稳定性验算

1、天然状态（未做防护）：

本次模拟工况为按设计边坡坡率（第一级1:0.75，第二级1:1，第三级1:1.25）开挖完成后的边坡，未加固防护下的状态。计算得安全系数为1.12，最终形成的整体塑性应变图如下所示：

图10：整体塑性应变云图

通过上图可以看出，边坡整体稳定性较好，且坡脚处位移变形最大，坡顶位移最小，近乎为0。

2、开挖完成后（防护做好）：

本次模拟工况为按设计边坡坡率（第一级1:0.75，第二级1:1，第三级1:1.25）开挖完成后，同时按照设计要求，做完锚杆节点防护。计算得安全系数为1.3，最终形成的整体位移云图如下所示：

图11：整体位移云图

通过上图可以看出，边坡整体稳定性较好，在锚杆的支护下，边坡整体稳定性得到进一步加强，最大位移出现在坡顶，仅为3.4cm，较好地验证了此次设计的合理性。

3结论

此次进行的科学研究，主要运用了“控制变量”法，采用了理正岩土计算软件，开展了一系列参数的科学研究。同时，采用Midas GTS NX软件进行辅助验证，所得结论很好地验证了本次设计的合理性与经济性。主要得出结论如下：

（1）坡率在1:1之前，边坡安全系数与边坡坡率之间存在线性关系，在1:1坡率之后，安全系数增加趋势增大，本次设计中第一级坡坡率按1:0.75,第二级坡坡率按1:1，第三级坡率按1:1.25较为合理。

（2）在边坡稳定分析中，岩土体的C值对边坡稳定性的影响要大于φ值，在实际工程中应优先保证岩土体的C值不受环境影响。

（3）本次装配式锚杆框格梁设计中的锚杆最优的长度、角度、粘结长度、水平间距分别为：12m、20°、12m、3m。

参考文献：

[1]张颖钧.装配式锚杆框架护坡的研究和设计[J].岩土工程学报,1993(04):77-82.

[2]张立志,王殿波,黄承权.装配式钢筋混凝土框架毛石结构防洪堤护坡[J].东北水利水电,2003(08):30-37.

[3]陈宾,李旻航,潘泽忠,向蓉,张亮. 一种装配式锚杆框格梁[P]. 湖南：CN105200997A,2015-12-30.

[4]王闯，梁晓丹，宋宏伟.锚杆支护在土木工程中应用的现状与发展[J].安徽建筑，2002,12(01):71-73.

[5]程良奎.岩土锚固的现状与发展[J].土木工程学报2001,34(03):7-12,34.

[6]杜估峥，苗子臻，邱浩然.岩土锚固理论研究现状与发展[J].工业技术创新，2016,03(04):635-638.

[7]张季如，唐保付.锚杆荷载传递机理分析的双曲函数模型[[J].岩土工程学报，2002,24(02):188-192.

[8]尤春安.全长粘结式锚杆的受力分析[[J].岩石力学与工程学报，2000,19(03):339-341.

[9] R W James, C Delaguardia. C R Mccreary. Strength of epoxy-grouted anchor bolts inconcrete[J]. Journal of Structural Engineering-ASCE.1987,113(12):2365-2381.

[10] Delhomme F, Debicki G. Numerical modeling of anchor bolts under pullout and relaxationtests[J]. ConstrBuildMater.2010,24(7):1232-1238.

[11]尤春安，战玉宝.预应力锚索锚固段的应力分布规律及分析[J].岩石力学与工程学报，2005,24(06):925-928.