核电厂补水工况下管道三通应力强度与疲劳分析方法研究

核电厂补水工况下管道三通应力强度与疲劳分析方法研究

杨妍

国家电投集团电能核电设备有限公司 264000

摘 要：目前我国已是世界第三核电大国，核电在我国的清洁能源中具有重要的地位。在运行核电厂中，由于系统水容量要求，或者水化学浓度要求等，经常存在补水需求。当补水温度和原管道中的水温存在较大温差时，可能在管道中引起严重热分层，叠加冷冲击和温度不连续的影响，导致管道三通应力强度不满足规范要求且累积疲劳因子过大，影响管道的使用寿命和电厂的正常运行。本文研究了一种疲劳优化分析方法，对于存在严重热分层的管道，考虑分层温差沿管道截面非中心对称分布，使用ANSYS三维计算稳态力矩；对于存在局部温度不连续的部件建立其三维实体模型，分区域施加瞬态参数，精确考虑冷冲击和温度不连续效应；根据ASME规范NB-3200进行疲劳评定。本文的优化分析方法有效避免了热分层和局部温度不连续的过度保守量，使得部件应力强度满足规范要求，且累计疲劳因子较常规计算方法大幅减小。本文的研究结果可用于核电厂补水引起管道三通疲劳问题的处理，也为类似管道的疲劳分析提供了参考方法。

关键词：疲劳分析，热分层，局部温度不连续，三维计算。

1引言

管道三通是一种常用的管道配件，具有改变流体流向、混合不同介质的作用，广泛应用于核电厂管路中。三通管件总体结构不连续，受到介质流动、流体压力、管道热膨胀、冷热流体掺混等复杂边界的影响，易产生破坏或断裂，严重影响核电厂的安全运转。因此，三通管件的应力强度和疲劳问题受到了国内外学者的广泛关注。

薛林锋[1]针对厚壁Y型三通管件，基于ASME标准中的分析计算方法，开展了静强度分析、热应力分析和热-结构耦合分析，对三通管在循环载荷下的强度进行了评估。邹智鑫[2]等人利用 T型三通管冷热流体掺混数值模拟以及钱锦烨等人[3]研究了不锈钢T型三通的内壁疲劳开裂问题，发现部分裂纹穿透三通管壁。试验研究表明，管道内高温水注入低温水中会形成掺混区域，使三通下游管壁产生交变热应力，管道焊缝在残余应力和热应力共同作用下产生热疲劳开裂。Utanohara等人[4]和Miyoshi等人[5]为了精确评估高低温流体掺混对三通管件热疲劳的影响，提出了针对T型三通管的流固耦合数值仿真方法，能够有效计算三通管管壁的温度波动。基于计算得到的温度波动，分析了三通管热应力变化情况，并基于热应力波动的时间历程以及雨流计数法，评估了三通管件的累计损伤。Zhang等人[6]采用ANSYS分析软件，先利用计算流体动力学方法计算流体混合时的流体压力和管壁温度，然后将该结果作为输入条件进行三通管的热应力分析，定量评估了T型三通的高周疲劳强度。

核电厂存在一些高温管道布置在低温设备顶部的情况，当出于系统水容量要求，或者水化学浓度要求需要往设备中补充低温水时，设备中的低温水进入高温管道，会在整个管系中形成明显的热分层[7]，产生交变热应力；同时，在距离低温设备较近的三通处，由于低温设备的影响，会出现冷冲击和温度不连续现象。热分层、冷冲击、温度不连续等因素综合影响下，可能导致管道三通应力强度不满足规范要求，且累积疲劳因子过大，影响管道的使用寿命和电厂的正常运行[8]。

目前广泛采用的管道应力强度和累计疲劳因子分析方法中[9]，难以精确处理热分层、冷冲击、温度不连续等因素的影响。对于热分层，常规分析中假设管道三通所在的水平段存在最大温差，并且温度沿管道截面线性分布；对于冷冲击和局部温度不连续现象，认为主管侧温度阶跃变化，支管侧保持低温。以上的处理过于保守，得到的应力和累计疲劳因子往往远高于实际值，既不能准确表征管道三通的应力状态，还可能造成不必要的经济损失。

针对以上问题，本文提出了一种针对补水工况下管系热分层、冷冲击和局部温度不连续的优化分析方法，有效避免了常规分析方法中的过度保守估计，能够正确计算管道应力和累积疲劳因子。本文研究的优化分析方法也可推广至其他承受热分层、冷（热）冲击和局部温度不连续部件的应力强度和疲劳分析工作，具有重要的理论和工程意义。

2优化计算方法

管道三通在热分层、冷冲击和温度不连续等因素的作用下，受到稳态应力和瞬态应力。其中，稳态应力由三通所在管路系统的整体热变形引起，瞬态应力由温度、流体压力等瞬变参数引起。因此，影响管道三通应力和疲劳分析结果的有三个主要因素：稳态力矩项以及瞬态参数中的瞬态项、压力项。其中，压力项受热分层、冷冲击以及局部温度不连续等因素的影响很小，对应力强度和疲劳分析结果的影响可以忽略，主要针对稳态力矩项和瞬态项进行优化。

2.1稳态力矩项优化方法

在目前常用的分析方法中，根据保守原则，假设管道三通所在的水平段存在最大温差，且分层温差沿管道截面线性分布，将其作为温度边界条件开展关系的热应力分析，得到管道三通处的稳态力矩范围。然而，研究管道介质热分层数据发现，分层温差沿管道截面并非中心对称分布：在补水的初始阶段集中在管道下部，随着补水进行缓慢向上发展，后期稳定以后热分层主要集中在管道上部。为了准确得到热分层影响下管路三通的稳态力矩应力范围，建立管系的三维模型，将管道横截面分为4层区域，如图1所示，按照热分层温差沿管道截面非中心对称分布，即DT

i（i=1-4）不同进行计算，其中DTi的值由热分层监测数据得到。

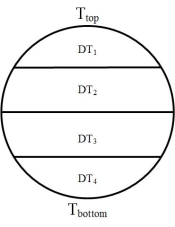
图1管道截面分区域示意图

2.2瞬态应力项优化方法

当管道边界条件比较简单时，可根据ASME NB-3600提供的分析方法评估三通处的瞬态应力[9]：

              (1)

公式中，、和为三通管件的二次应力指数，为管道外径，为管道截面惯性矩，t为管道名义壁厚，为使用压力范围，为设计机械载荷的组合产生的合成力矩，为室温下在总体结构不连续或材料不连续的两侧的平均弹性模量，和为a、b两侧的平均温度范围，和为室温下a、b两侧的热膨胀系数。

然而，管道三通受到冷冲击和局部温度不连续的影响，平均温度范围和难以精确计算。通常情况下，按照主管侧温度阶跃变化、支管侧保持低温进行计算，得到的瞬态应力远超实际值，既不能正确反应三通管的真实应力状态，还可能造成不必要的经济损失。为实现三通处瞬态应力的精确计算，建立三通的三维实体模型，并且将内表面分成五个区域，分别施加温度时程进行计算，利用得到的三维温度场开展热应力分析。

2.3疲劳损伤累积法则

根据疲劳损伤积累理论，若工件在k个应力水平Si作用下，各经受ni次循环，累积疲劳因子D为

                   (2)

公式中，ni是在应力Si的循环次数，可通过雨流法统计得到；Ni是在应力Si下循环到破坏的寿命，由S-N曲线确定。

根据线性累积损伤理论，破坏准则为

                           (3)

当D大于或等于1时，代表工件发生疲劳失效。

3方法验证

以某核电厂平衡管为例，建立管系的三维模型，根据现场监测数据，沿管道横截面施加不同比例的热分层温度分布，计算了管系热分层产生的稳态热膨胀载荷；然后建立了三通管的三维实体模型，分区域考虑补水瞬态的影响；叠加三维计算得到的热载荷，进行详细的三维应力计算，并根据NB-3200进行应力和疲劳评定。

3.1稳态力矩项计算

在ANSYS Workbench中建立三通所在管系的三维有限元模型，为了准确施加温度边界，将管系沿轴向分为七段，每段施加不同的温度工况，如图2所示；并沿管道截面分为四段，如图1所示，每段施加不同的DTi，并且每段内再划分5层，按照温度线性变化进行考虑。根据实际测量的热分层监测数据，取较为保守的温差分布工况，轴向分段的温度工况见表1，截面方向分段的工况见表2。从表1可以看出，冷却水在刚进入管道时有比较明显的热分层，随着冷热水的的混合，管道下游几乎不存在温差。

图2 管系三维模型及轴向分段示意图

表1 管道轴向的温度工况

表2 温差沿管道截面的分布比例

根据表1和表2的温度边界条件，开展管道的静力学仿真，管系的变形如图3所示，最大位移约为26 mm。在模型上取截面，截面1是三通管件与主管相连的面，计算该截面受到的载荷，如表3所示。

图3 补水工况下管系热变形云图

表3 截面1的载荷

利用表3得到的载荷，可以进一步计算三通管件的稳态力矩应力范围(Moment Stress Range, MSR)，将结果与优化前计算方法(假设管道三通所在水平段存在最大温差)进行对比，可以发现，采用优化后的计算方法得到的稳态力矩应力范围显著降低。

表4 稳态力矩应力范围计算结果

3.2瞬态应力项计算

简单工况下可以根据公式(1)计算管件的瞬态应力项，然而补水工况下的三通管边界条件复杂，难以准确评估平均温度范围和，只能按照主管侧温度阶跃变化、支管侧保持低温进行计算，得到的应力值远高于真实值。为了解决这一问题，建立三通管的三维实体模型，开展三通管的热分析，然后根据热分析得到的温度场计算三通管的瞬态热应力，从而得到准确的瞬态应力项。

利用ANSYS ICEM软件为三通管划分网格，为了保证计算结果的精度，全部采用结构单元，并将三通管的内表面分为五个区域，如图4所示。针对补水工况，根据实际监测结果，为三通管施加温度时程，如表5所示。

图4 三通管网格划分与分区示意图

表5 三通管件的温度时程

不同温度瞬态下三通管的温度分布如图5所示，当时间为200 s、即表5中第4个温度瞬态时，温差产生的热应力最大，应力分布如图6所示。

图5 不同温度瞬态下三通管温度分布 (a) t=10 s，(b) t=60 s，(c) t=200 s，(d) t=20000 s

图6 补水工况下三通管最大瞬态热应力

基于有限元分析得到的热应力，根据ASME NB-3200计算三通管的局部一次薄膜应力PL、一次弯曲应力Pb和二次应力Qm，并将其与优化前的结果进行对比，发现计算值显著降低。

表6 瞬态应力结果对比

根据以上计算结果，对管道三通进行疲劳分析。首先基于计算得到的交变应力强度，利用设计疲劳曲线确定允许的最大重复次数，即公式(2)中的Ni；其次采用雨流法，获得实际的应力循环次数ni；最后，根据公式(2)计算累积疲劳因子。在核电厂60年寿命周期中，需要进行320次补水，320次补水工况下累积疲劳因子为0.9252，满足设计需求。

4总结

本文从应力强度和疲劳分析的流程和主要影响因素出发，分析了补水工况下三通疲劳分析不满足规范要求的主要原因，解决了两个关键问题。一是通过管系的三维计算，模拟沿管道截面非中心对称分布的热分层温度，计算了管系整体热分层产生的载荷，在保证适当保守性的基础上，载荷小于按照中心对称的分层温度分布计算得到的结果；二是通过三维计算，将三通的三维实体模型分区域分别施加瞬态参数，避免了常规计算中由于无法精确考虑冷冲击和局部温度不连续而导致的过度保守量，同时保证了计算的准确性和正确性。

本文的研究结果已应用于核电厂正常运行期间补水引起的平衡管疲劳分析，保障了电厂正常运行期间补水的时间节点，避免了因应力不满足规范或者补水次数用尽而停堆。本文研究的优化分析方案也可推广至其他承受热分层、冷（热）冲击和局部温度不连续部件的疲劳分析工作，具有重要的工程意义。

参考文献

[1]薛林锋，基于ASME Ⅷ2-2017 Y型三通热-结构耦合分析及疲劳分析 [J]. 中国化工装备, 2019, 21(02): 20-23+27.

[2]邹智鑫, 王合旭, 蒋彦龙, 李泽伟. T型三通管冷热流体掺混数值模拟 [J]. 计算机辅助工程, 2019, 28(01): 46-52.

[3]钱锦烨, 关凯书. EO/EG装置不锈钢T型三通热疲劳开裂失效分析 [J]. 压力容器, 2019, 36(11): 51-57.

[4]Utanohara Y, Miyoshi K, Nakamura A. Conjugate numerical simulation of wall temperature fluctuation at a T-junction pipe [J]. Mechanical Engineering Journal, 2018, 5(3):

[5]Miyoshi K, Nakamura A, Utanohara Y, Kamaya M. Numerical simulation of thermal stress fluctuation at a mixing tee for thermal fatigue problems [J]. Mechanical Engineering Journal, 2018, 5(4):

[6]Garrido O C, El Shawish S, Cizelj L. Study of the quantitative assessment method for high-cycle thermal fatigue of a T-pipe under turbulent fluid mixing based on the coupled CFD-FEM method and the rainflow counting method [J]. Nuclear Engineering and Design, 2017, 318: 274-275.

[7]郭德朋;陆道纲;冯预恒. 核电厂管线中的热分层现象 [J]. 原子能科学技术, 2007, 5: 570-574.

[8]王昕;钱才富. 非锚固式大型立式熔盐储罐热疲劳分析 [J]. 压力容器, 2018, 035(004): 31-35.

[9]  1998 Edition through 2000 Addenda, ASME Boiler and Pressure Vessel Code, Section III