四川省西昌市凉山州民族中学 615000
在高中阶段,运用正、余弦定理构造关于三角形边角的方程,是求解三角形问题的基本方法。对于解三角形问题的客观题,如果借助平面几何知识,有时更为简单、直观有效,人教A版《必修5》1.1节的“探究与发现”运用几何法理解、解读结论,充分体现了数形结合的思想。我们可以通过对称变换、旋转伸缩变换,以及直线和圆的几何知识转化问题,以便实现求解三角形。
一、构造直线(射线)、圆
例1.在![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,则下列对三角形解的个数的判断正确的是( )
,则下列对三角形解的个数的判断正确的是( )
A.![]() ,
,![]() ,
,![]() ,有两解
,有两解
B.![]() ,
,![]() ,
,![]() ,有一解
,有一解
C.![]() ,
,![]() ,
,![]() ,无解
,无解
D.![]() ,
,![]() ,
,![]() ,有两解
,有两解
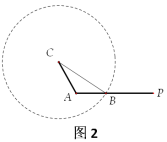
【分析】选项都是已知边![]() ,
,![]() 和角
和角![]() ,画出角
,画出角![]() ,取点
,取点![]() 满足
满足![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,判断圆
,判断圆![]() 与射线
与射线![]() 有几个公共点(不包括点
有几个公共点(不包括点![]() ).选项A,C,D情形如图1,选项B情形如图2.对选项B,因
).选项A,C,D情形如图1,选项B情形如图2.对选项B,因![]() ,则只有一公共点,故B正确.
,则只有一公共点,故B正确.

例2.在锐角![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
![]() ,则
,则![]() 的最大值是( )
的最大值是( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【分析】如图,在锐角![]() 中,过
中,过![]() 作直线
作直线![]() 垂直
垂直![]() 于点
于点![]() ,
,
因![]() ,
,![]() ,所以
,所以![]() ,在射线
,在射线![]() 上
上
取点![]() ,使得
,使得![]() ,则
,则![]() ,
,
所以![]() ,故D正确.
,故D正确.
例3.在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,则线段
,则线段![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
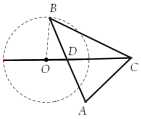 【分析】在
【分析】在![]() 中,设
中,设![]() ,由题意得
,由题意得![]() ,
,
根据阿波罗尼斯圆的定义,点![]() 在以射线
在以射线![]() 上一点
上一点![]() 为圆心,
为圆心,
![]() 为半径的圆上(如图),且
为半径的圆上(如图),且![]() 的面积为1,
的面积为1,
则![]() ,即
,即![]() ,故选C.
,故选C.
例4.设锐角![]() 的内角
的内角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() ,则
,则![]()
![]() 的取值范围为( )
的取值范围为( )
A.(1,9] B.(3,9] C.(5,9] D.(7,9]
 【分析】
【分析】
由正弦定理![]() (
(![]() 为
为![]() 的外接圆半径),
的外接圆半径),
再由余弦定理可得![]()
![]()
![]() ,
,
如图,由对称性可知当点![]() 位于劣弧
位于劣弧![]() (不含
(不含![]() )
)
时![]() 为锐角三角形,
为锐角三角形,![]() ,
,![]() ,则
,则![]()
![]() 的范围为(7,9],故选D.
的范围为(7,9],故选D.
例5.已知△ABC为锐角三角形,D,E分别为AB、AC的中点,且CD丄BE,则cosA的取值范围是
 A.
A.![]() B.
B.![]() C.[
C.[![]() D.
D.![]()
【分析】
设![]() 交于点
交于点![]() ,连接
,连接![]() ,延长交
,延长交![]() 于
于![]() ,则
,则![]() 为
为![]() 的
的
中点,由直角三角形与重心的性质可得![]() ,不妨设
,不妨设
![]() ,则点
,则点![]() 在以
在以![]() 为圆心,3为半径的劣弧
为圆心,3为半径的劣弧![]() (不含
(不含![]() )上(如图).
)上(如图).![]() ,
,![]() ,由对称性可知
,由对称性可知![]() 的取值范围为
的取值范围为![]() ,故选D.
,故选D.
二、对称、旋转构造
 例6.如图,已知
例6.如图,已知![]() 是半径为1,圆心角为
是半径为1,圆心角为![]() 的扇形,点
的扇形,点![]() 分别是半径
分别是半径![]() 及扇形弧上的三个动点(不同于
及扇形弧上的三个动点(不同于![]() 三点),则
三点),则![]() 周长的最小值是( )
周长的最小值是( )
A.![]() B.
B.![]()
B.C.![]() D.
D.![]()
【分析】
先根据对称性将边BC,边AC转移,再根据三角形三边在一直线时周长最小的思路即可解答.
作点C关于线段OQ,OP的对称点C1,C2.连接CC1,CC2.
 则C△ABC=C1B+BA+AC2≥C1C2.
则C△ABC=C1B+BA+AC2≥C1C2.
又∵C1C2=![]()
而∠C1OC2=∠C1OQ+∠QOC+∠COP+∠POC2
=2(∠QOC+∠POC)=2∠QOP=150°
∴![]()
 =
=![]() =
=![]() .
.
∴△ABC的周长的最小值为![]() .
.
故选B.
例7.如图所示,在平面四边形![]() 中,
中,![]() ,
,
![]() ,
,![]() 为等边三角形,则
为等边三角形,则![]() 面积的最大值为_______.
面积的最大值为_______.
 【分析】将
【分析】将![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 得
得![]() ,将
,将![]() 视为定
视为定
点,由题意可知点![]() 的轨迹是以定点
的轨迹是以定点![]() 为圆心,3为半径的圆.
为圆心,3为半径的圆.
故点![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,则
,则![]() 面积的最
面积的最
大值为![]() .
.
通过上述各例题的解答分析,发现从几何角度解决类似的三角形求解的客观题,能较为形象直观的获得正确答案,但对思维层面要求较高,设定相应的定点(三角形的部分角的顶点),确定动点(角的顶点)的轨迹的能力要求较高。在平常的教学中,应该引领学生用发散的眼光对问题进行观察、分析、探索、提炼,提高学生直观想象能力的核心素养。
第4页