基于杠杆法计算八速自动变速器的速比

基于杠杆法计算八速自动变速器的速比

江兴宝

130224197805216216

摘要：液力自动变速器采用行星齿轮结构，通过不同的构架获得不同的速比。行星齿轮机构的传动比的优化关系到传动系统的效率，并且决定了开发的难度以及成本的投入。本文通过某8AT对速比计算方法进行说明。

关键词：液力自动变速器  行星齿轮系 等效杠杆法  速比计算

一 引言

自动变速器在未来的几年里还将会保持相当大的市场占有率，其中最成熟，使用最为广泛的是液力自动变速器（AT）。AT采用了行星齿轮机构，从挡位来说已经由最初的4挡到目前的8挡、9挡甚至是10挡。随着档位的不断增加，行星排的数量以及连接方式都会改变，作为最基础的，速比的计算是很关键的。本文针对市场上某款8AT通过等效杠杆法进行速比的计算。

二 等效杠杆法的说明

(1) 行星排的构成：

行星排由太阳轮、行星轮、齿圈和行星架通过一定的关系组合在一起。

(2) 行星排的种类：

按排数不同可分为单排和双排行星齿轮系；按行星齿轮组数的不同可分为单级和双级行星排；

图1单排单级行星系       单排双级行星系

(3) 速比获得的方法

在行星系计算中有一个转速特性关系式：

单级：ns+KnR-(1+K)npc=0   （1）

双级：ns-KnR+(1-K)npc=0   （2）

以上K=ZR/Zs行星排特性参数

ns太阳轮转速ZS 太阳轮齿数

nR  齿圈转速     ZR   齿圈齿数

npc行星轮转速

由式（1）（2）可知，固定任何一个元件，指定输入输出，都能得到输入与输出的比值，即速比。比如单级行星排固定行星架，即npc=0，太阳轮输入，齿圈输出，便能得到速比值为：ns/nR=-K；

K为固定正值，“-”代表方向相反，此时档位为倒挡。为了直观通常把行星排通过传动简图形式表现出来：

图2  传动简图

通过转速特性关系式可得到不同的输入、输出及制动状态下的速比，

图3  (a)  （b）       （c）

    （d）   （e）      （f）

速比如下表：

（4）等效杠杆

杠杆法是将行星排等效为一根三（多）

点的杠杆，通过比例关系计算速比；

单级排的等效杠杆：

图4 a结构图 b简化图  c等效杠杆图

双级排的等效杠杆：

图5 a结构图 b简化图   c等效杠杆图

（5）计算速比

前文通过特性公式计算了一种形式的速比，即单级单排固定行星架，太阳轮输入，齿圈为输出。

         图6 单级单排行星排速比计算

上图，通过三角关系，得到：

          速比=n入/n出=K/1=K

方向与输入方向相反为倒挡。与通过特性公

式计算的结果相同。

（6）单级双排的等效杠杆

     分别将前排和后排等效为三支点的两个

杠杆，然后根据结合关系将节点连接并合并，

得到一个四支点单排杠杆。下图中前排K1和

后排K2都是单级排，K1行星架与K2齿圈连

接，K1齿圈与K2行星架连接。K1太阳轮为

输入，K2行星架输出，K2太阳轮制动。

图7 行星排简图

等效杠杆：

图8 杠杆图

（7）典型行星排的等效杠杆

    目前市场上很多行星系都是在辛普森

式行星排和拉维娜式行星排基础上构型的。

图9 a辛普森 b拉维娜

辛普森行星排等效杠杆如下图：

图10辛普森行星排杠杆图

拉维娜行星排等效杠杆如下图：

图11 拉维娜行星排杠杆图

三 多档AT速比的计算

现以一款8AT为例介绍速比的计算方法

       图12 结构剖视图

（1）结构分析

图13示意图

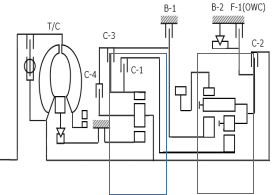将上图简化成如下图：

前排 后排

图14 结构简图

可知产品有四个离合器C1-C4，两个制动器B1，B2，单向离合器F-1及两个行星排组成。前排为单排双级、后排为前文介绍的拉维娜式行星排。整个机构输入为前排行星架，输出为后排的齿圈。

（2）速比计算

计算时把前排作为固定速比，根据不同结合状态与后行星排速比相乘。

①对行星排进行杠杆简化

  图15 简化杠杆图

  ② 各元件功能及动力流向

           图16 动力流向图

分析其结构，前太阳轮固定，前排行星架输入，后排齿圈输出。C1连接前齿圈和拉维娜后排太阳轮，C2连接前行星架和拉维娜行星架，C3连接前齿圈和拉维娜前排太阳轮，C4连接前行星架和拉维前太阳轮。B1固定拉维娜前太阳轮，B2和F-1连接拉维娜行星架。通过以上可得:

图17  简化杠杆图

③ 用直线连接各元件，得到与输出轴的交点

图18 元件连接图

上图可得到输出轴上10个交点，基准横轴上8个，轴下2个，考虑倒挡速比的大小，舍弃纵轴最下端的一点。这种结构是8个前进档，1个倒档。档位使用的元件如下：

④速比计算

              图19   速比图

上图以一档为例进行速比的计算：

已知K1=82/38;K2=74/34；K3=74/30,

假设nin=1,nout为一档转速

首先计算前排减速比：

nout/nin=LS1-R1/LS1-PC1

即nout/nin=（K1-1）/KI，

则：nout=（K1-1）/K1            （3）

然后计算后排速比，通过三角关系得：

n1/nout=1/K3，那么n1=1/K3×nout（4）

（3）（4）可得：

n1=1/K3×（K1-1）/K1             （5）

那么i1=K1K3/(K1-1)              （6）   

将K1,K3值带入（6）中可得一档速比i1=4.596

同样方法计算出其他档位速比:

以上转速可用excel计算得出。

四 结束语

(1)  采用等效杠杆法对8AT速比进行计算，

 结果与产品说明上的速比信息吻合；

(2)  在使用杠杆法时，行星排简化，动力流   

向分析尤为重要，一定要仔细确认，不然

很容易出现错误的结果。

(3) 本文更详细的说明了杠杆法的使用方法，更适合初学者进行参考。

以上，本文参考了一些前辈的著作和论文，在此特别感谢。

参考文献：

[1]高惠民. 杠杆法分析皇冠8速自动变速

器传动比. 汽车维修与保养.2018.3

[2]于杰、马朝锋、郭奶超、刘凯.基于杠杆

法的4行星排传动方案综合. 机械传

动.2019.5

[3]张鹏飞.基于杠杆法的拉维纳式变速器传

动方案分析.汽车零部件.