广东电网有限责任公司汕尾供电局
摘要：用电量增长是经济发展的晴雨表。从用电结构上看，一半以上的用电户，用电量随季节的波动性特别明显，尤其是对于居民用户来讲更如此。因此对于以居民用户为主的用电结构，一般来说，夏秋季用电量偏高，冬春季用电量偏低。并且大部分产业、行业的用电量也存在着较为明显的季度性特征。本课题根据前期多年的历史用电量数据，采用考虑长期趋势的回归方程法，预测出下一年度内各月度的用电量，并给出了详细的预测方法。
关键词：长期趋势;回归;用电量
一、背景
季节性是每年相同时间段出现相同幅度和方向的波动。由于气温季节、传统节假日等因素的影响，很多时间序列具有季节效应，比如某景点的旅客人数、每月的气温、每月的空气污染指数、每月的商品销售额等都会呈现明显的季节变动规律。
用电量增长是经济发展的晴雨表。从用电结构上看，一半以上的用电户，用电量随季节的波动性特别明显，尤其是对于居民用户来讲更如此。因此对于以居民用户为主的用电结构，一般来说，夏秋季用电量偏高，冬春季用电量偏低。并且大部分产业、行业的用电量也存在着较为明显的季度性特征。
二、技术方案
为了量化季节成分，本课题使用季节指数的概念，即用简单平均法来计算周期内各时期季节性影响的相对数。季节分析的方法很多，这里介绍两种方法，一种是不考虑长期趋势的季节指数法；另一种是考虑长期趋势的回归方程法消除法。
（一）不考虑长期趋势的季节指数法。以月度数据为例，给出季节指数的计算方法：第一，对各年相同月份的数据求平均，得到各月平均数。第二，计算所有月份数据的总平均数。第三，用各个月份的月平均除以总平均数就是各月的季节指数。季节指数反映了该月份与总平均值之间一种比较稳定的关系，如果这个比值大于1，说明该月份的值常常会高于总平均值，如果该比值小于1，说明该季度的比值常常低于总平均值，如果序列的季节指数都近似为1，说明该序列没有明显的季节效应。
（二）考虑长期趋势的回归方程法。如果序列中长期趋势特征非常明显，为准确反映现象随季节变动的特征，应先消除长期趋势的影响。长期趋势的消除方法很多，比如移动平均法、回归方程法等，这里仅介绍回归方程剔除法。这种方法假设乘法模型，即Yt=Tt×St×It。回归方程法的具体步骤如下：
第一，建立yt与t的线性回归模型，利用最小二乘法求出回归拟合值yˆt。
第二，用观察值yt除以拟合值yˆt剔除原时间序列中的长期趋势的回归方程；
第三，计算剔除长期趋势之后的时间序列yt/yˆt的同期平均值；
第四，用yt/yˆt的同期平均值除以yt/yˆt的总平均值，得到季节指数；
第五，根据回归方程，得到当期电量值，再乘以相应的季节指数，即可得到各期的预测电量。
本课题采用第二种方法，即考虑长期趋势的回归方程法。
三、数据分析过程
1、取得原始数据。使用H县2013年-2021年的每月电量（亿度）。
年度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
2013 | 0.8059 | 0.8075 | 0.6145 | 0.8295 | 0.8330 | 0.9303 | 1.0551 | 1.1540 | 1.2179 | 0.9936 | 0.9556 | 0.8442 |
2014 | 0.9382 | 0.6798 | 0.9464 | 0.9835 | 0.9500 | 1.0625 | 1.2259 | 1.4709 | 1.4569 | 1.3966 | 1.1502 | 0.9975 |
2015 | 1.0124 | 1.1472 | 0.8424 | 1.0574 | 1.1435 | 1.1883 | 1.4846 | 1.4998 | 1.5529 | 1.3471 | 1.1780 | 1.0686 |
2016 | 1.0511 | 1.1095 | 0.9220 | 1.2352 | 1.0981 | 1.2890 | 1.5310 | 1.7031 | 1.5345 | 1.4264 | 1.3029 | 1.1222 |
2017 | 1.1300 | 1.1947 | 0.9587 | 1.1926 | 1.2042 | 1.3438 | 1.5699 | 1.7243 | 1.9248 | 1.7529 | 1.6273 | 1.3131 |
2018 | 1.3327 | 1.4155 | 1.1352 | 1.4042 | 1.3959 | 1.8023 | 1.7212 | 1.7283 | 1.6872 | 1.4699 | 1.2420 | 1.1387 |
2019 | 1.1728 | 0.9594 | 1.2237 | 1.2495 | 1.3751 | 1.6425 | 1.8837 | 1.8970 | 1.7155 | 1.5040 | 1.2309 | 1.2894 |
2020 | 1.1594 | 0.9336 | 1.1950 | 1.1783 | 1.5812 | 1.8143 | 2.2061 | 1.9611 | 1.8503 | 1.5276 | 1.3752 | 1.5244 |
2021 | 1.4307 | 1.0463 | 1.4454 | 1.5091 | 2.0818 | 1.9573 | 2.3074 | 2.2554 | 2.2798 | 1.8235 | 1.5075 | 1.5485 |
2、分析原始数据的变化趋势。
可以看出，H县的各月份用电量非常有规律，有长期线性增长的趋势，而且季节性非常明显。
3、建立yt与t的线性回归方程，利用最小二乘法求出回归拟合值yˆt。在当前WPS、Excel中，都支持直接取得该回归方程。
根据历史数据，求出线性回归方程为yt=0.0077t-9.4632。
其中回归系数0.0077为正数，与拟合直线的趋势相符。
得出各月份拟合值电量（亿度）。
年度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
2013 | 0.9010 | 0.9087 | 0.9164 | 0.9241 | 0.9318 | 0.9395 | 0.9472 | 0.9549 | 0.9626 | 0.9703 | 0.9780 | 0.9857 |
2014 | 0.9934 | 1.0011 | 1.0088 | 1.0165 | 1.0242 | 1.0319 | 1.0396 | 1.0473 | 1.0550 | 1.0627 | 1.0704 | 1.0781 |
2015 | 1.0858 | 1.0935 | 1.1012 | 1.1089 | 1.1166 | 1.1243 | 1.1320 | 1.1397 | 1.1474 | 1.1551 | 1.1628 | 1.1705 |
2016 | 1.1782 | 1.1859 | 1.1936 | 1.2013 | 1.2090 | 1.2167 | 1.2244 | 1.2321 | 1.2398 | 1.2475 | 1.2552 | 1.2629 |
2017 | 1.2706 | 1.2783 | 1.2860 | 1.2937 | 1.3014 | 1.3091 | 1.3168 | 1.3245 | 1.3322 | 1.3399 | 1.3476 | 1.3553 |
2018 | 1.3630 | 1.3707 | 1.3784 | 1.3861 | 1.3938 | 1.4015 | 1.4092 | 1.4169 | 1.4246 | 1.4323 | 1.4400 | 1.4477 |
2019 | 1.4554 | 1.4631 | 1.4708 | 1.4785 | 1.4862 | 1.4939 | 1.5016 | 1.5093 | 1.5170 | 1.5247 | 1.5324 | 1.5401 |
2020 | 1.5478 | 1.5555 | 1.5632 | 1.5709 | 1.5786 | 1.5863 | 1.5940 | 1.6017 | 1.6094 | 1.6171 | 1.6248 | 1.6325 |
2021 | 1.6402 | 1.6479 | 1.6556 | 1.6633 | 1.6710 | 1.6787 | 1.6864 | 1.6941 | 1.7018 | 1.7095 | 1.7172 | 1.7249 |
4、用观察值yt除以拟合值yˆt剔除原时间序列中的长期趋势；
年度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
2013 | 0.8944 | 0.8886 | 0.6706 | 0.8977 | 0.8940 | 0.9902 | 1.1139 | 1.2086 | 1.2653 | 1.0240 | 0.9771 | 0.8564 |
2014 | 0.9444 | 0.6790 | 0.9382 | 0.9676 | 0.9275 | 1.0296 | 1.1792 | 1.4045 | 1.3810 | 1.3142 | 1.0746 | 0.9252 |
2015 | 0.9324 | 1.0491 | 0.7650 | 0.9536 | 1.0241 | 1.0569 | 1.3115 | 1.3160 | 1.3534 | 1.1662 | 1.0131 | 0.9130 |
2016 | 0.8921 | 0.9356 | 0.7725 | 1.0282 | 0.9083 | 1.0594 | 1.2504 | 1.3823 | 1.2377 | 1.1434 | 1.0380 | 0.8886 |
2017 | 0.8893 | 0.9346 | 0.7455 | 0.9219 | 0.9253 | 1.0265 | 1.1922 | 1.3019 | 1.4448 | 1.3083 | 1.2076 | 0.9689 |
2018 | 0.9778 | 1.0327 | 0.8235 | 1.0131 | 1.0015 | 1.2859 | 1.2214 | 1.2198 | 1.1843 | 1.0262 | 0.8625 | 0.7865 |
2019 | 0.8058 | 0.6557 | 0.8320 | 0.8451 | 0.9252 | 1.0994 | 1.2545 | 1.2569 | 1.1309 | 0.9864 | 0.8033 | 0.8372 |
2020 | 0.7491 | 0.6002 | 0.7644 | 0.7501 | 1.0017 | 1.1437 | 1.3840 | 1.2244 | 1.1497 | 0.9446 | 0.8464 | 0.9338 |
2021 | 0.8723 | 0.6349 | 0.8730 | 0.9073 | 1.2458 | 1.1660 | 1.3682 | 1.3313 | 1.3396 | 1.0667 | 0.8779 | 0.8977 |
5、计算剔除长期趋势之后的时间序列yt/yˆt的同期平均值
月度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
同期平均值 | 0.8944 | 0.8886 | 0.6706 | 0.8977 | 0.8940 | 0.9902 | 1.1139 | 1.2086 | 1.2653 | 1.0240 | 0.9771 | 0.8564 |
同时，可求出：总平均值=
=1.0245。
6、用yt/yˆt的同期平均值除以总平均值，得到季节指数。
月度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
季节指数 | 0.8631 | 0.8037 | 0.7792 | 0.8985 | 0.9602 | 1.0691 | 1.2229 | 1.2630 | 1.2458 | 1.0824 | 0.9436 | 0.8685 |
7、检验季节指数的可靠性。
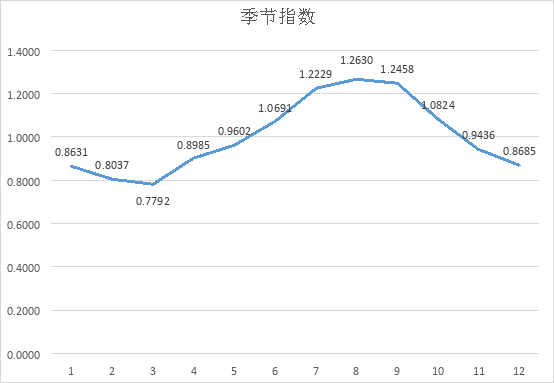
数据趋势基本上反映了电量变化趋势，因此此季节指数分析结果较为可靠。
8、预测未来12的电量。
将12个月的时间t代入回归方程y=0.0077t-9.4632来预测趋势成分；然后让趋势成分乘以1-12月的季节指数，就得到未来12个月的电量的预测值。
年度 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
2022 | 1.7326 | 1.7403 | 1.7480 | 1.7557 | 1.7634 | 1.7711 | 1.7788 | 1.7865 | 1.7942 | 1.8019 | 1.8096 | 1.8173 |
可以看出预测值较好的结合了历史数据，能够对未来做合理的预测。
四、总结
H县用电量增长数据具有较强的季节趋势，在近十年中，也具有明显的长期线性增长趋势，属于典型的周期性增长经济活动。
通过使用考虑长期趋势的回归方程法，能够比较合理地预测各个月度的用电量。
参考文献：
[1]王预.数据分类分析和预测技术的应用[J].高性能计算技术,2010,(4):37-41.
[2]杨正瓴,翟祥志,尹振兴,等.超过指数增长速度的年度用电量曲线拟合预测[J].天津大学学报,2008,(11).
[3]赵凯利.时间序列组合预测模型在我国居民消费价格指数中的应用[D].兰州交通大学,2016.61.
[4]汤成友,郭丽娟,王瑞.水文时间序列逐步回归随机组合预测模型及其应用[J].水利水电技术,2007,(6).
[5]于世刚,王利,杜鹏.大连市年用电量预测模型优化研究[J].资源开发与市场.2014,(12).
[6]丁屹峰,程浩忠,江峰青,等.不同增长趋势下中长期电量预测组合优化灰色模型[J].上海交通大学学报,2003,37(9):1355-1357,1371.
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网 琼ICP备2021005105号
