瞄准误差对金相显微镜物镜放大倍数误差不确定度的影响

瞄准误差对金相显微镜物镜放大倍数误差不确定度的影响

黄璐琦

陕西省计量科学研究院 710000

摘要：本文通过理论分析计算了在不同物镜放大倍率下的瞄准误差（对准误差和调焦误差）的大小，并以5X物镜放大倍率为例，具体分析计算了金相显微镜物镜放大倍率误差的不确定度，旨在为金相显微镜物镜放大倍数误差不确定度的评定提供参考。

关键词：金相显微镜、物镜放大倍数、瞄准误差、不确定度

1引言

金相显微镜具有稳定性好、成像清晰、分辨率高、视野大而平坦等特点，而被广泛用于各种金属和合金材料表面金相组织、微观结构以及热处理后相位组织的识别和分析，同时在化学领域中，对各种硫化物及氧化物的尺寸、粒径分布和数量大小的计算也发挥了极其重要的作用^[1]。因此，作为金相显微镜主要计量特性物镜放大倍数误差的准确与否对其在实际计算应用中就显得尤为重要。

本文主要通过研究瞄准误差对金相显微镜物镜不同放大倍数误差测量结果不确定度的影响，并结合具体的理论计算对其进行测量结果不确定度的评定。

2瞄准误差

在目视瞄准的测量系统中，测量人员目视对准产生的瞄准误差是其测量误差中的一个重要误差成分^[2]。在光学测量技术方面，瞄准误差分为对准误差和调焦误差。对准误差是指垂直于瞄准轴方向上，使目标和比较标记重合或置中过程中产生的误差，又称为横向误差。调焦误差是指目标和比较标记沿瞄准轴方向重合或置中产生的误差，又称为调焦误差。

2.1对准误差

依据JJF 1914—2021《金相显微镜校准规范》的规定，在对物镜放大倍数误差进行校准的过程中，需将标准刻线尺的刻线与10×十字分化目镜的刻线对齐重合读数（如下图1），但是由于人眼的极限，两条刻线不可能完全重合对齐，这就会在垂直于瞄准轴方向上引入一个对准误差^[3]。

图1两条刻线的压线对准

当通过放大倍率为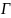 的金相显微镜观察时，对准误差 为：

（1）

式中： ——人眼的瞄准精度（′）；

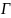——金相显微镜整体放大倍率；

由于采用压线瞄准，取瞄准精度 =1′，则在物镜不同放大倍率下的对准误差如下表1所示：

表1 物镜在不同放大倍数下的对准误差

2.2调焦误差

在进行校准读数前需调节合适的焦距，使得标准玻璃线纹尺在金相显微镜目镜视野范围内清晰成像，此时会在瞄准轴方向上引入一个调焦误差^[4]。

当通过放大倍率为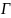 的金相显微镜观察时，对准误差 为：

（2）

式中： ——人眼的瞄准精度（′）；

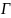——金相显微镜整体放大倍率；

n——金相显微镜物方折射率；

NA——金相显微镜物镜数值孔径；

——照明光波长（μm）；

这里，取人眼瞄准精度 =1′，物镜物方折射率n=1.5，照明光波长λ=0.555 μm，NA取物镜的实际标称值，则在物镜不同放大倍率下的对准误差如下表2所示：

表2 物镜在不同放大倍数下的调焦误差

3物镜放大倍数误差测量结果不确定度的评定

以下将以5X物镜放大倍率为例，来具体地分析计算物镜放大倍数误差测量结果的不确定度。

3.1测量方法

以1mm标准玻璃刻线尺和10×十字分划目镜组合进行金相显微镜物镜放大倍数误差的测量^[5]。将1mm标准玻璃线纹尺置于金相显微镜的载物台上，调节金相显微镜物镜与标准玻璃刻线尺间的像面距离，使得标准玻璃线纹尺在金相显微镜目镜视野范围内清晰成像。然后取下金相显微镜原有的目镜，换装上10×十字分划线目镜，以10×十字分划尺目镜刻线与标准玻璃刻线尺像的相应刻线不重合的偏差值与标准玻璃刻线尺所用间距的像对应目镜分划尺标称长度的比值，作为金相显微镜放大倍数误差。

3.2测量模型

金相显微镜物镜放大倍数误差的计算公式为：

（3）

式中： ——物镜放大倍数误差

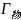——物镜放大倍数

——标准玻璃刻线尺所用间距的像在目镜分划尺上的实际长度

——标准玻璃刻线尺所用间距的标称长度

3.3方差和灵敏系数

由公式（3）得：

（4）

3.4标准不确定度一览表

表3 标准不确定度一览表

3.5标准不确定度的评定

3.5.1 10×十字分划目镜刻线误差引入的不确定度

使用10×十字分划目镜测量时， 其引入的不确定主要由分划目镜刻线的最大允许误差决定^[6]。分度值为0.1mm的十字分划目镜的MPE为5μm，，按照均匀分布，在5×物镜下所用刻度范围为5mm，其相对标准不确定度为：

（5）

3.5.2测量读数不准引入的不确定度

该项不确定度分量包含标准玻璃线纹尺刻线不准引入的不确定度、测量时对准误差引入的不确定度、调焦误差引入的不确定度以及相应被测刻线测量时的估读误差引入的不确定度。

①标准玻璃线纹尺刻线不准引入的不确定度

所用1mm标准玻璃线纹尺刻线的MPE为±2μm，按照均匀分布，在5×物镜下所用刻度范围为1mm，其相对标准不确定度为：

（6）

②对准误差引入的不确定度

由上文可知，对准误差为1.460μm，按均匀分布，在5×物镜下所用刻度范围为5mm，其相对标准不确定度为：

（7）

③调焦误差引入的不确定度

由上文可知，调焦误差为19.633μm，按均匀分布，在5×物镜下所用刻度范围为5mm，其相对标准不确定度为：

（8）

④估读误差引入的不确定度

估读误差为10×十字分划目镜刻线分度值的1/10，即1mm的1/10，即区间半宽度a=0.1mm，按均匀分布，在5×物镜下所用刻度范围为5mm，其相对标准不确定度为：

（9）

四项合并：

（10）

3.6合成不确定度的评定

（11）

3.7扩展不确定度的评定

取k=2，则扩展不确定度为：

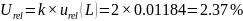（12）

4结论

当金相显微镜物镜放大倍率为5×时，其相对扩展不确定度为2.37%，包含因子k=2。

金相显微镜物镜放大倍数误差不确定度主要来自于目镜分划尺刻线误差、标准玻璃线纹尺刻线误差、对准误差、调焦误差以及刻线测量时估读误差。当物镜放大倍率为5X时，调焦误差对其结果不确定度的影响较大，该项误差不可忽略。而对准误差对其结果不确定度的影响较小，可忽略不计。

参考文献

[1]郭可信. 金相学史话(6):电子显微镜在材料科学中的应用[J]. 材料科学与工程, 2002.

[2]李建芳, 王君. 光学测量技术[M]. 西安电子科技大学出版社, 2013.

[3]陈家汉. 常用长度计量仪器的仪器误差与测量过程误差(五)[J]. 计量技术, 1999.

[4]朱耀升. 光学测量与仪器对准精度的基本公式[J]. 应用光学, 1983, 000(005):19-33.

[5] JJF 1914-2021 金相显微镜校准规范. 国家质量监督检验检疫总局.

[6] JJF 1950.1-2012 测量不确定度评定与表示. 国家质量监督检验检疫总局.