柱下独基与墙下条基相交处的基底面积设计研究

柱下独基与墙下条基相交处的基底面积设计研究

李遥扬

中船第九设计研究院工程有限公司 上海 200090

摘要：如果柱下独基和墙下条基相交处出现面积重叠导致基底面积减小，会直接影响到建筑物整体的稳定性，对工程质量产生影响。为解决此问题，下文对柱下独立基础的计算方法和墙下条形基础的计算方法进行简要说明，综合思路对柱下独立基础与墙下条形基础相交处的基底面积设计方案进行简要分析。

关键词：柱下独基；墙下条基；相交处；基底面积

前言：在目前砖混结构的建筑中，通常使用的是墙下条形基础，并且依照纵横墙体中所承受的荷载力对其宽度进行计算，但如果建筑物中存在柱下独立基础，则两者相连区域可能会出现互相重叠的情况，进而造成基底面积减小。

1.柱下独立基础验算方法

为方便体现柱下独立基础的计算方法，将柱下条形基础的受力情况虚构如图1。再利用倒梁方法将其计算方法进行简化。地基反力的计算过程为q=（FA+FB+FC+FD+FE）/L=(150+1300+2000+2000+1300)/25.55=265kN/m²。其中该条形基础的弯矩设计值为MA,MB,MC,MD，其中MA计算过程为0.5*ql²=65，MB计算过程为0.5*ql²/11=108.4，MC计算过程为0.5*ql²=590.2，MD计算过程为0.5*ql²=463.7。该柱下独立基础宽为150cm，地基梁宽为50cm，翼板外部厚度为25cm，采用C30号混凝土，HEB335钢筋。根据上述计算可得出基底净反力设计值应当在q/b=265/1.5=176.7.该设计值应当小于地基承载力。

柱下独立基础的斜截面抗剪强度应当根据净反力设计值进行计算，h=V/0.7f=176.7/0.7*1.43=176.5，该数值小于规范中的250，所以该柱下独立基础的翼板厚度可以满足抗剪强度。

图 1 柱下独立基础受力情况

2.墙下条形基础验算方法

墙下条形基础上方通常为砖混结构的墙体，所以条形基础的基底面积应当根据上方承重墙的荷载力F来决定，并且地面还会给墙下条形基础提供反方向的力P。P指的就是由上方承重墙给基底施加的反作用力，也叫净反力。如果将墙体长度设定为1m，那么净反力应当依照F/l*b进行计算，其中的F等于上述柱下独立基础的q=265，所以其受到的净反力P应当为176.7kpa。为方便对计算过程进行论述，将墙下条形基础的宽度虚构为150cm，梁宽为50cm，翼板外部边缘厚度为25cm，采用的也是C30号混凝土和HRB335钢筋。那么墙下条形基础的斜截面抗剪切力计算应当为P*(b/2)=176.7*1.5=132.5，其中的b为墙下条形基础的基础宽度，单位换算为m。再根据V/0.7F=132.5/0.7*1.43=132，该数值小于规范250，所以该墙下条形基础的翼板外部边缘厚度符合要求。

从计算流程来看，不论是柱下独立基础的基底面积还是墙下条形基础的基底面积都应当符合上述验算方式，只有在保证受力符合相关规范后，才能开始进行相交处基底面积的设计，下文就根据此标准，简要分析如何设计柱下独立基础和墙下条形基础相交处的基底面积。

3.柱下独立基础与墙下条形基础相交处基底面积设计方案

在对柱下独立基础和墙下条形基础相交处基底面积设计的过程中，必须要考虑到基底压力的重叠，通常双方的排列是纵横方向，由于墙体会受到竖向的荷载力，所以在墙下条形基础和柱下独立基础相交处会存在竖向应力扩散传递现象，并在相交处产生应力集中，远离相交处时，应力会恢复正常。根据此种特点，在对两者相交处基底面积进行设计时，应当对应力集中区域的面积进行修正，对于距离相交处较远的部位还是按照之前的方式进行设计。以此为思路，下文简要说明设计相交处基底面积的方案。

3.1尺寸设计

根据地基基础设计规范的要求，相交处设计应当满足公式

（1）

其中F为墙体上方传至相交面积处的竖向荷载力设计值。

其中G为该墙体和柱体自重设计值。

其中A为柱下独立基础和墙下条形基础相交处基底面积。

其中f为项目中的地基承载力设计值。

为最大限度保障工程质量，基底面积在符合公式（1）的条件下，还应当通过两种验算方法，进而保证基底面积完全符合地基基础设计规范要求。为方便体现计算过程，将埋置深度设置为d，回填土重度为γ，γ通常取值为20kN。则得出公式

（2）

将公式（2）带入至公式（1）中可以得出公式

（3）

对于柱下条形基础，为方便计算将长度取为1m，再将公式（3）转换为公式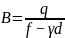 （4）

其中B指的是柱下独立基础的宽度。

其中q指的是柱下独立基础的竖向荷载力设计值。

由上述公式（4）可以得出，柱下独立基础宽度B和柱下独立基础的竖向荷载设计值q为正相关。根据上述中荷载力的扩散传递作用，将墙下条形基础宽度设置为B2，根据公式可以看出，B、B2的面积和荷载力q成正比，根据上述数量关系，可以将柱下独立基础和墙体条形基础的尺寸公式设计成：

（5）

其中l1和l指的是柱下独立基础和墙下条形基础相交面积的边长。

其中B1和B指的是柱下独立基础和墙下条形基础相交面积的宽度。

为修正常数。

3.2修正常数的确定

就以柱下独立基础和墙下条形基础的相交方式为L型为例，根据上述中的公式（4）和公式（5）可以得出相交部分的面积计算公式为

（6）

将L型相交的两侧受力位置设置为q1和q2。竖向力计算公式为

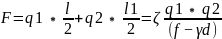（7）

将公式（6）和公式（7）带入到公式（3）中可以得出该修正常数为1。这代表的就是在墙体条形基础和柱体独立基础相交方式为L型时候，只要双方都能通过荷载力验算，符合相关地基规范可以不需要对其进行修正。

根据上述，如果是双方相交形式为T型或者十字型时，根据上述公式互相代入得出在T型相交时该常数值应当小于1.5。如果是十字型相交该常数值应当小于2。所以，在对柱下独立基础和墙下条形基础相交基底面积进行设计时，应当根据上述计算公式进行修正，最终依照公式（3）确定相交基底面积。

结论：综上所述，为最大限度保障工程质量，以荷载力扩散传递作为原理，确定柱下独立基础和墙下条形基础相交部分应符合哪些受力标准，上文中公式结果简洁明了，避免因基底重合导致受力不合理，进而对工程质量起到增强作用。

参考文献：

[1]明茂刚. 集中荷载下条形基础弹性地基梁法地基承载力计算及应用[J]. 工程技术研究,2020,5(13):257-258+262.

[2]吕玺琳,薛大为. 土体软化条件下条形基础地基承载力数值模拟[J]. 岩土工程学报,2019,41(S2):9-12.