武汉市常青第一中学
“立足基础,稳重求变,重在素养”是近几年高考的主要特征,在紧扣教材把握考纲要点的同时,平稳又不乏创新,在圆锥曲线的考察上,也是比较稳定,突出考核价值,重视数学素养,体现学科本质,本文主要将圆锥曲线中一类有关定值的问题进行方法探析。
在圆锥曲线问题中,学生更多的利用直线与圆锥曲线的关系通过联立解决问题,这是解析几何学生需要掌握的的基本的技能要求,圆锥曲线中的很多问题,是利用韦达定理得到两根之间的关系,来处理有关![]() 、
、![]() 或
或![]() 、
、![]() 的对应量。
的对应量。
我们知道韦达定理是![]() 、
、![]() 、
、![]() 、
、![]() 的整体关系,在解决问题是可利用设而不求的办法将问题转化为韦达定理的代入问题,但有些问题中,将问题转化为根的关系式之后,发现根并没有对称的出现,本文将这种问题称为非对称问题,对于非对称问题,本文将总结几种处理非对称问题的常见方法。
的整体关系,在解决问题是可利用设而不求的办法将问题转化为韦达定理的代入问题,但有些问题中,将问题转化为根的关系式之后,发现根并没有对称的出现,本文将这种问题称为非对称问题,对于非对称问题,本文将总结几种处理非对称问题的常见方法。
法一、利用方程解决问题
例1 ![]() 是椭圆
是椭圆![]() 的左右顶点,过点
的左右顶点,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,其中
两点,其中![]() 在
在![]() 轴的上方,设
轴的上方,设![]() ,证明:
,证明:![]() 为定值.
为定值.
解析:设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立消去
,联立消去![]() 可得
可得![]() ,又因为
,又因为![]() ,由
,由![]() 的代入化简之后的结果可以看出,直接利用韦达定理代入已不能解决问题,变量
的代入化简之后的结果可以看出,直接利用韦达定理代入已不能解决问题,变量![]() 与
与![]() 是不对称的,因为
是不对称的,因为![]() ,由椭圆方程可知,
,由椭圆方程可知,![]() ,则
,则![]() ,所以
,所以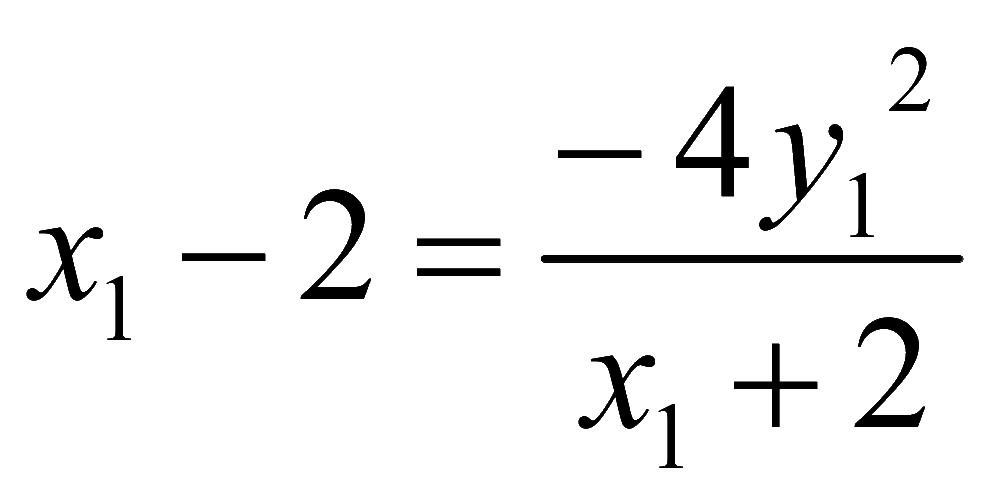 ,所以
,所以![]() 化简为对称式,可由韦达定理代入进行进一步的运算。
化简为对称式,可由韦达定理代入进行进一步的运算。
另解:利用椭圆方程还可以求![]() ,因为
,因为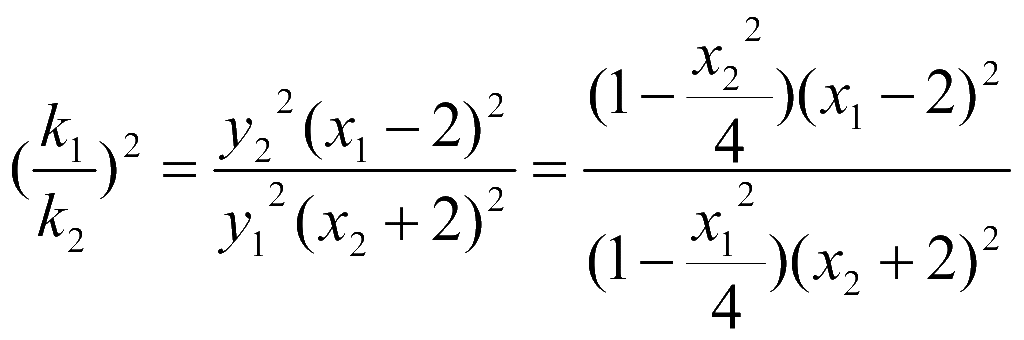 即
即![]() ,由韦达定理代入可证明为定值。
,由韦达定理代入可证明为定值。
变式 已知椭圆![]() ,
,![]() 为左右顶点,动直线
为左右顶点,动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,设点
两点,设点![]() 在
在![]() 轴上方,设
轴上方,设![]() 交于一点
交于一点![]() ,求证:点
,求证:点![]() 的横坐标为定值。
的横坐标为定值。
解析:联立直线与椭圆方程消去![]() 可得:
可得:![]() ,所以
,所以 ,直线
,直线![]() ,直线
,直线![]() ,所以
,所以![]() ,所以
,所以![]() ,因为点
,因为点![]() 在椭圆上,所以
在椭圆上,所以![]() ,故
,故![]() ,所以
,所以![]() ,至此,又回到对称型的韦达定理,可用直接代入解得定值为4
,至此,又回到对称型的韦达定理,可用直接代入解得定值为4
点评:此方法的关键是构造出因式分解的结构,利用椭圆方程,将不对称式子局部代换使其成为对称式。这种解法的优势是计算量较小,但是局限性也很明显,需要因式分解的结果与椭圆方程的变形结果相同才可使用,适用于与椭圆顶点相关的问题。
法二、整体代换消元
例2 已知![]() 分别为椭圆
分别为椭圆![]() 的右、上顶点,
的右、上顶点,![]() 在椭圆上,且
在椭圆上,且![]() .记直线
.记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值.
为定值.
解析:设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立可得:
,与椭圆方程联立可得:![]()
![]() ,可见结果非对称,需对结果再进行化简。消去
,可见结果非对称,需对结果再进行化简。消去![]() 得
得 ,化简到这个式子之后,就需要利用换元思想,将分子分母的统一的化简成由
,化简到这个式子之后,就需要利用换元思想,将分子分母的统一的化简成由![]() 表示,可得
表示,可得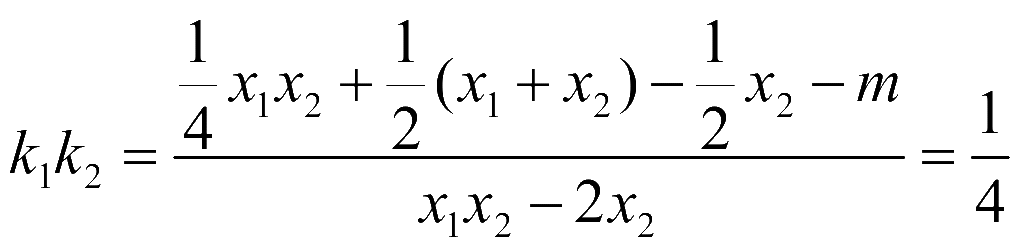
变式 对于例![]() ,同样可以整体代换,可得
,同样可以整体代换,可得![]() 即
即
点评 此方法的巧妙之处在于利用韦达定理消去变量![]() 留下
留下![]() ,整体对比发现分式上下成倍数,在处理证明恒成立问题时此方法可使用。特别适用于定值问题的处理,适用范围较广。
,整体对比发现分式上下成倍数,在处理证明恒成立问题时此方法可使用。特别适用于定值问题的处理,适用范围较广。
法三、配凑法化非对称为对称
例3 设椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 为倾斜角为
为倾斜角为![]() ,
,![]() ,求离心率的取值范围。
,求离心率的取值范围。
解析 设![]() ,由
,由![]() 可得,
可得,![]() ,构造
,构造![]() 及
及
![]() ,两式相乘可得
,两式相乘可得![]() ,再设直线方程,消去
,再设直线方程,消去![]() 得关于
得关于![]() 的一元二次方程,由韦达定理代入就可得到离心率与参数
的一元二次方程,由韦达定理代入就可得到离心率与参数![]() 之间的关系,可得离心率的取值范围。
之间的关系,可得离心率的取值范围。
变式 设直线![]() 过点
过点![]() ,和椭圆
,和椭圆![]() 顺次交于
顺次交于![]() 两点,求
两点,求![]() 的取值范围。
的取值范围。
解析:设直线![]() 的方程为:
的方程为:![]() ,联立椭圆方程消去
,联立椭圆方程消去![]() 得:
得:![]() ,则
,则
 ,由于
,由于![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,由
,由![]() 可得
可得![]() ,故有
,故有![]() ,从而有
,从而有![]() ,所以
,所以![]() 。
。
点评:![]() 经常出现在圆锥曲线的题型为:过顶点
经常出现在圆锥曲线的题型为:过顶点![]() 的直线与圆锥曲线交于
的直线与圆锥曲线交于![]() 两点,满足
两点,满足![]() 或者
或者![]() ,用坐标表示之后,构造韦达定理的结构,构建方程,便可解决问题。
,用坐标表示之后,构造韦达定理的结构,构建方程,便可解决问题。
法四、 统一变量法化解非对称问题
例4 已知椭圆![]() ,点
,点![]() 分别为椭圆的左右顶点,过点
分别为椭圆的左右顶点,过点![]() 的直线
的直线![]() 交椭圆与
交椭圆与![]() 两点,
两点,![]() 的中点为
的中点为![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ;求证:
;求证:![]() 为定值。
为定值。
解析:因为![]() 三点共线,设
三点共线,设![]() ,
,![]() ,则
,则![]() ,即
,即![]()
所以 ,解得:
,解得: ,又因为
,又因为![]()
又因为![]()
![]() ,代入
,代入![]() 式可得定值为
式可得定值为![]()
变式 对于例![]() ,因为
,因为![]() 三点共线,设
三点共线,设![]() ,代入坐标可得
,代入坐标可得![]() ,所以
,所以![]() ,又因为
,又因为![]() ,故
,故![]() ,又因为
,又因为![]() ,解得
,解得![]() ,
,![]() ,带入可得
,带入可得![]()
点评 统一变量法是利用参数,将多个变量划归为一个变量,是参数方程的解题思路,适用于直线过定点的问题,但计算量较大,综合计算能力要求较高。