基于BP神经网络的财务风险预测问题探究

基于 BP 神经网络的财务风险预测 问题探究

张莹

四川瑞鼎商品混凝土有限公司 617062

摘要：随着我国经济的快速发展，企业财务方面出现诸多问题，企业财务面临着巨大的风险，需要对于风险问题有及时的预测机制。企业发生财务危机是一个逐步显现、缓慢恶化的过程,它的发生具有一定的先兆,因此具有可预测性.为了规避和防范财务风险,企业有必要对财务风险进行充分的认识和分析。本文在深入分析财务预测面临的关键问题和比较各种财务风险预测方法的基础上，探讨利用BP神经网络对财务风险进行分析和预测的可行性。

关键字：BP神经网络、财务风险、预测

引言：投资越大风险越大，如何建立一个精确度和运算速度相对较高的股市预测模型对于金融投资者具有重大理论意义和实际应用价值。将人工神经网络应用到财务风险预测上面成为一个新的趋向。建立三层 BP 神经网络并且分析收敛速度，得到当选择的数据合理且具有很好的性质时，拟合效果会更加准确。从而说明BP神经网络对于财务风险的预测具有可行性和合理性，进而对提高企业的工作效益做出帮助。

一、构建BP神经网络

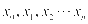神经网络中最基本的元素就是神经元了，中心位置的第 个神经元接收到了 个来自于其他神经元的信号 ，并且两两神经元之间的连接权重分别为 ，这些值要在神经元内部汇总求和，具体方式为 与相对应的 相乘求和。然后与神经元内部已经设置好的阈值进行比较，再通过激活函数 计算得出结果。

我们设置的BP神经网络隐含层只为一层，其中的输入端信号是 ，我们将这些需要研究的指标量 作为了输入层的输入之后，便可以设置隐藏层各个节点的函数输入：

；

而进入计算之后的函数输出可以表示为：

其中隐藏层中 是作用公式，具体表示为： ；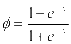

输出层的输入方程表示为：

；

输出层的输出方程表示为：

；

我们将 作为了隐藏层各结点的输入，那么可以通过它将输出值 表示为：

；

因为输出层的 ，所以输出层各结点的输出可以表示为：

；

我们由上诉的公式得到了预测的初始值 ，在前期几次得到的及结果不符合期望，我们又重新运用误差的反向传播对权值和阈值进行了一定的调整。

其中输出层的二次型误差函数： ；

全部的总误差： ；

在知晓误差计算后，我们随后分别对 进行带公式计算，我们可以求得对应的四个调整值：

；

输出层的权值调整公式为：

；

输出层阈值调整公式为：

；

隐藏层阈值调整公式为：

；

；

我们又因为知道

；

；

；

再通过各类不同的调整公式得到结果：

；

；

；

；

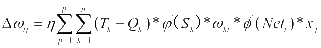经过了一系列的调整以及反复误差循环，我们便得到了预测值误差在期望范围内的预测值结果。

2. 利用BP神经网络预测风险

从财务风险预警方法的应用角度出发，建立BP神经网络模型，将已知时间区间的数据当作训练集，对模型的预估数据和实际数据相对比，得到对应的相对误差，计算变动趋势值。接着，针对训练集的结果，对测试集，也就是后续预测的区间进行模拟仿真，以此我们可以得到消除了原本有滞后影响的预测值，并使得预测结果不断地通过神经网络学习进一步更新。

建立好了BP神经网络之后，作者随机选取了1500家上市公司的财务数据作为仿真实验的数据源﹐利用Matlab软件工具进行仿真实验,实验结果表明,当BP神经网络的隐含层数从一层增加到三层时﹐神经网络的学习精度﹑学习速率都有较为明显的改善﹐说明本实验建立的具有三个隐含层的多层BP神经网络模型具有较为合理的网络结构,其收敛速度﹑精准度都有较大提升。

2. BP存在的问题

3.1局部最小化

从数学角度看，传统的 BP神经网络为一种局部搜索的优化方法，它要解决的是一个复杂非线性化问题，网络的权值是通过沿局部改善的方向逐渐进行调整的，这样会使算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。加上BP神经网络对初始网络权重非常敏感，以不同的权重初始化网络，其往往会收敛于不同的局部极小。

3.2算法收敛速度慢

由于BP神经网络算法本质上为梯度下降法，它所要优化的目标函数是非常复杂的。由于优化的目标函数很复杂，它必然会在神经元输出接近0或1的情况下，出现一些平坦区，在这些区域内，权值误差改变很小，使训练过程几乎停顿。BP神经网络模型中，为了使网络执行BP算法，不能使用传统的一维搜索法求每次迭代的步长，而必须把步长的更新规则预先赋予网络，这种方法也会引起算法低效。

参考文献

1. 杨水燕.企业财务风险预警方法应用浅析[J].行政事业资产与财务,2021,(16):100-101

2. 王海峰.试论企业财务管理中的风险预测及处理——基于优化的BP神经网络算法[J].中国注册会计师,2018,(09):103-106

3. 赖茂涛.基于BP神经网络算法的企业财务风险预测方法研究[J].微型电脑应用,2021,37(12):155-157