福建省晋江市子江中学 362261
摘要:构造函数是解决抽象不等式的基本方法,根据题设的条件,并借助初等函数的导数公式和导数的基本运算法则,相应地构造出辅助函数。通过进一步研究辅助函数的有关性质,借助函数与方程思想,转化与化归思想,给予巧妙的解答。
引言
抽象函数不等式的求解及求参数的取值范围是的一类重点问题,解决这类问题的主要方法是根据条件与结论间的结构特征,联想到基本初等函数的导数和导数的四则运算法则,“构设”出相应的抽象函数,然后求导,利用抽象函数的单调性、奇偶性以及相关的性质进行求解. 下面就高中数学一些常见的、典型的数学例题作简单归纳。
【例1】(2021天津二模)设f(x),g(x)在[a,b]上可导,且f'(x)>g'(x),则当a
A.f(x)>g(x) B.f(x)
C.f(x)+g(a)>g(x)+f(a) D.f(x)+g(b)>g(x)+f(b)
【解析】 ∵f'(x)>g'(x)
∴[f(x)-g(x)]'>0, ∴f(x)-g(x)在[a,b]上是增函数.
∴f(a)-g(a)g(x)+f(a).
【点睛】(1)若已知xf'(x)+f(x)的符号,则构造函数g(x)=xf(x);一般地,若已知xf'(x)+nf(x)的符号,则构造函数 。
。
(2)若已知xf'(x)-f(x)的符号,则构造函数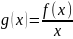 ;一般地,若已知xf'(x)-nf(x)的符号,则构造函数
;一般地,若已知xf'(x)-nf(x)的符号,则构造函数 。
。
(3)若已知f'(x)+f(x)的符号,则构造函数 ;一般地,若已知f'(x)+nf(x)的符号,则构造函数
;一般地,若已知f'(x)+nf(x)的符号,则构造函数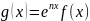 。
。
(4)若已知f'(x)-f(x)的符号,则构造函数 ;一般地,若已知f'(x)-nf(x)的符号,则构造函数
;一般地,若已知f'(x)-nf(x)的符号,则构造函数 。
。
【例2】f(x)是定义在(0,+∞)上的非负可导函数,且满足xf'(x)-f(x)≤0,对任意正数a,b,若a
A.af(b)≤bf(a) B.bf(a)≤af(b)
C.af(a)≤bf(b) D.bf(b)≤af(a)
【解析】设函数 ,则
,则
∵ x>0,xf'(x)-f(x)≤0,
∴ F'(x)≤0,故函数F(x)在(0,+∞)上为减函数或为常值函数.又由0 ,则bf(a)≥af(b).
【例3】(2021南昌第二次调研)已知函数f(x)是定义在R上的偶函数,设函数f(x)的导函数为f'(x),若对任意的x>0都有2f(x)+xf'(x)>0成立,则( ).
A.4f(-2)<9f(3) B.4f(-2)>9f(3)
C.2f(3)>3f(-2) D.3f(-3)<2f(-2)
【解析】根据题意,令g(x)= ,则g'(x)=2xf(x)+
,则g'(x)=2xf(x)+ f'(x),
f'(x),
因对任意的x>0都有2f(x)+xf'(x)>0成立,
则当x>0时,g'(x)=x[2f(x)+xf'(x)]>0恒成立,
即函数g(x)在(0,+∞)上为增函数.
又由函数f(x)是定义在R上的偶函数,
则f(-x)=f(x),则g(-x)= f(-x)=
f(-x)= f(x)=g(x),
f(x)=g(x),
即函数g(x)也为偶函数,
则g(-2)=g(2),且g(2)
故选A.
【例4】已知定义域为R的函数f(x)满足f(4)=-3,且对任意的
x∈R总有f'(x)<3,则不等式f(x)<3x-15的解集为 .
【解析】令g(x)=f(x)-3x+15,则g'(x)=f'(x)-3<0,
∴ g(x)在R上是减函数.又g(4)=f(4)-3×4+15=0,
∴ 不等式f(x)<3x-15的解集为(4,+∞).
【点睛】 利用导数比较大小或解不等式的常用技巧
利用题目条件,构造辅助函数,把比较大小或求解不等式的问题转化为先利用导数研究函数的单调性问题,再由单调性比较大小或解不等式。
【例5】(本题为多项选择题)(2021新泰市第二中学高三模拟)已知定义在 上的函数f(x),f'(x)是f(x)的导函数,且恒有
上的函数f(x),f'(x)是f(x)的导函数,且恒有
cosxf'(x)+sinxf(x)<0成立,则( ).
A. B.
B.
C. D.
D.
【解析】根据题意,令g(x)= ,
,
则g'(x)= ,
,
又 ,且恒有cosxf'(x)+sinxf(x)<0,
,且恒有cosxf'(x)+sinxf(x)<0,
则g'(x)<0,即函数g(x)在上单调递减.
由于  ,故有
,故有  , 即
, 即  ,
,
化简可得  ;
;
又由于  ,故有
,故有 ,即
,即  ,
,
化简可得  .
.
综上可知,选CD.
【例6】(2021石家庄第一次质检)已知函数f(x)=ln x,
 (a≠0).
(a≠0).
(1)若函数h(x)=f(x)-g(x)存在单调递减区间,求实数a的取值范围;
(2)若函数h(x)=f(x)-g(x)在[1,4]上单调递减,求实数a的取值范围.
【解析】(1)由题意得 ,x∈(0,+∞),
,x∈(0,+∞),
所以h'(x) ,
,
由于h(x)在(0,+∞)上存在单调递减区间,
所以当x∈(0,+∞)时, 有解,
有解,
即  有解.
有解.
设 ,所以只要a>G(x)min即可.
,所以只要a>G(x)min即可.
而G(x)min= .
.
所以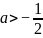 .
.
又因为a≠0,所以a的取值范围为( ,0)∪(0,+∞).
,0)∪(0,+∞).
(2)因为h(x)在[1,4]上单调递减,
所以当x∈[1,4]时,h'(x) 恒成立,
恒成立,
即 恒成立.
恒成立.
由(1)知 , 所以a≥G(x)max,
, 所以a≥G(x)max,
而G(x)max (此时x=4),
(此时x=4),
所以a≥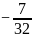 ,
,
又因为a≠0,所以a的取值范围是 ∪(0,+∞).
∪(0,+∞).
【点睛】根据函数单调性求参数的一般思路
(1)利用集合间的包含关系处理.函数y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集.
(2)函数f(x)为(a,b)上的增函数的充要条件是对任意的x∈(a,b)都有f'(x)≥0且在(a,b)内的任一非空子区间上,f'(x)不恒为零,应注意此时式子中的等号不能省略,否则漏解.
(3)函数在某个区间上存在单调区间可转化为不等式有解问题.
【例7】定义:设函数 在
在 上的导函数为
上的导函数为 ,若
,若 在
在 上也存在导函数,则称函数
上也存在导函数,则称函数 在
在 上存在二阶导函数,简记为
上存在二阶导函数,简记为 .若在区间
.若在区间 上
上 ,则称函数
,则称函数 在区间
在区间 上为“凹函数”.已知
上为“凹函数”.已知 在区间
在区间 上为“凹函数”,则实数
上为“凹函数”,则实数 的取值范围为
的取值范围为
【解析】根据“凹函数”的定义,对任意x∈(﹣1,+∞),
f''(x)=m +lnm﹣ln(x+1)﹣1>0都成立,
+lnm﹣ln(x+1)﹣1>0都成立,
同构为  ,
,
利用g(x)= 在(﹣∞,+∞)是增函数,
在(﹣∞,+∞)是增函数,
得不等式  ,
,
即  对任意x∈(﹣1,+∞)都成立,
对任意x∈(﹣1,+∞)都成立,
令 g(x)=ln(x+1)﹣x ,x∈(﹣1,+∞)
则  ,
,
 ,
, 单调递增;
单调递增;
 ,
, 单调递减,
单调递减, ,
,
即lnm>0,所以m>1,
【点睛】注意同构法在解题中的应用,对于常见形式的同构要熟练运用,如 。
。
总之,以抽象函数为背景,题设条件或所求结论中具有“f(x)±g(x),f(x)/g(x),f(x)g(x)”等特征式,旨在考查导数运算法则的逆向,变形应用能力的客观题,是近几年高考试卷中的一位“常客”,常以压轴题的形式出现,解答这类问题的有效策略是将前述式子的外形结构特征与导数运算法则结合起来,合理构造出相关的可导函数,然后利用该函数的性质解决问题。
参考文献
[1] 胡彬 一道不等式问题的释题解析[J];语数外学习(高中版高二年级);2007年11期
[2] 陈枫 解证不等式的常用方法[J];中学生百科;2009年14期
[3] 侯善领 浅析不等式性质在解题中的正确运用[J];高中数理化;2014年12期
2