江南机电设计研究所 贵州贵阳 550000
江南机电设计研究所 550000
摘要:针对目前导弹控制系统参数设计时完全依靠设计师主观经验,对所选取特征点的控制系统参数进行逐个‘试凑’整定的耗时、主观、不规范设计问题,本文研究了将粒子群算法(PSO)应用于导弹稳定控制回路参数自动化设计的方法,且针对标准粒子群算法在导弹稳定控制回路参数寻优中表现出收敛快、成功率低的问题,通过引入遗传算法中选择、交叉思想对标准粒子群算法进行了改进,形成粒子群-遗传算法(PSO-GA),扩大了解空间范围,成功解决了标准粒子群算法存在的缺点。通过对PSO算法及PSO-GA算法的研究,实现了导弹稳定控制回路的规范化、自动化设计,具有一定的实用价值。
主题词:粒子群算法 粒子群-遗传算法 稳定控制回路 自动化设计
引言
导弹稳定控制系统的设计,一般是在整个飞行空域内取一定数量的特征点,然后根据线性化数学模型,对每个特征点逐一进行控制回路参数设计。目前工程设计中,多采用人工‘试凑’的方法,进行多次循环反复设计和校验,直到凑出满足设计指标要求的控制器参数。这种依赖设计师工程经验,参杂了人为主观因素在内的设计,不仅不规范且耗时,若选取的特征点数量太多,仍然采用传统的人工设计方法,是一件非常繁杂且不可完成的任务。
本文研究了粒子群算法及其改进算法在导弹侧向稳定控制回路参数自动化设计中的应用,分别将PSO算法和PSO-GA算法用于某型导弹侧向稳定控制回路自动化设计,并将设计结果在六自由度中进行仿真验证,并与传统人工设计结果进行比较,证实了粒子群优化算法及其改进算法在导弹侧向稳定控制回路中设计的可行性。
粒子群算法及其改进
标准PSO算法
设在![]() 维目标搜索空间中有
维目标搜索空间中有![]() 个粒子,粒子
个粒子,粒子![]() 的空间位置为
的空间位置为![]() ,将
,将![]() 代入目标函数就可以计算出其适应度值,根据适应度值的大小衡量粒子
代入目标函数就可以计算出其适应度值,根据适应度值的大小衡量粒子![]() 的优劣。单个粒子所经历过的最优位置记为
的优劣。单个粒子所经历过的最优位置记为![]() ,整个粒子群经历过的最优位置记作
,整个粒子群经历过的最优位置记作![]() ,粒子根据公式(1)来更新自己的速度和位置:
,粒子根据公式(1)来更新自己的速度和位置:
![]() (1)
(1)
式中![]() 为加权系数也称动力常量,为非负数,代表了前一速度对当前速度的影响,本文采用自适应调整方法进行
为加权系数也称动力常量,为非负数,代表了前一速度对当前速度的影响,本文采用自适应调整方法进行![]() 设计,如式(2);
设计,如式(2);![]() 和
和![]() 为学习因子见式(3);
为学习因子见式(3);![]() 为第
为第![]() 个粒子的飞翔速度,
个粒子的飞翔速度,![]() ;
;![]() 为第
为第![]() 个粒子的位置;
个粒子的位置;![]() 为相互独立的随机数,服从
为相互独立的随机数,服从![]() 的均匀分布。
的均匀分布。
 (2)
(2)
 (3)
(3)
式中![]() 分别为当前迭代次数和最大迭代次数。
分别为当前迭代次数和最大迭代次数。
由于导弹侧向稳定控制回路参数设计具有多约束条件,计算结果表明:标准粒子群算法在对这种多约束条件下的复杂系统进行控制参数寻优时,由于其‘早熟’收敛特性,容易陷入局部极值,成功率低。
粒子群-遗传算法(PSO-GA)
遗传算法中交叉是以二进制码的形式进行,这样的操作需要进行二进制码生成和二进制解码操作,操作精度高,但额外增加了计算量。本文直接采用十进制数进行交叉操作,如式(4)。
式中,![]() 为标准PSO寻优结果,作为两个父代粒子,
为标准PSO寻优结果,作为两个父代粒子,![]() 、
、![]() 为经过选择的两个父代粒子进行交叉后得到的两个新粒子,
为经过选择的两个父代粒子进行交叉后得到的两个新粒子,![]() 为
为![]() 间的随机数。
间的随机数。
系统模型与目标函数
侧向稳定控制回路结构
本文采用复合稳定回路的结构形式,如图1:

稳定控制回路结构图
图中![]() 为控制指令,
为控制指令,![]() 为过载响应,
为过载响应,![]() 为侧向角速度,
为侧向角速度,![]() 、
、![]() 、
、![]() 和
和![]() 为调参参数。
为调参参数。
 (5)
(5)
舵偏角![]() 到角速度的传递函数为:
到角速度的传递函数为:
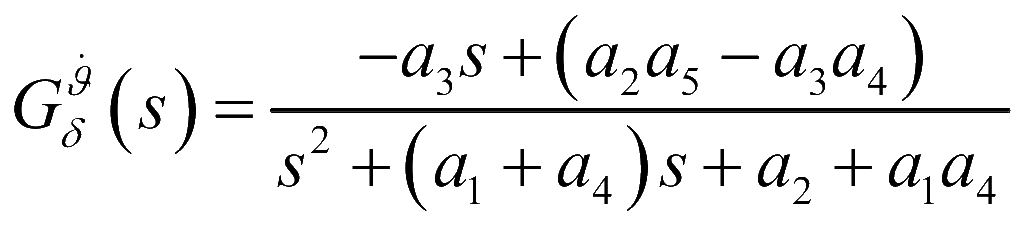 (6)
(6)
三阶期望特征多项式为:
![]() (7)
(7)
其中,参数![]() 、
、![]() 、
、![]() 为设计参数,本文利用PSO算法和PSO-GA算法进行自动寻优,从而解出调参系数
为设计参数,本文利用PSO算法和PSO-GA算法进行自动寻优,从而解出调参系数![]() 、
、![]() 、
、![]() 和
和![]() 。
。
目标函数
本文定义包含侧向稳定控制回路单位阶跃过载响应的超调量、上升时间、稳态误差、幅值裕度、相位裕度、侧向角速、舵偏角、舵偏角速度,来评价侧向稳定控制系统的综合性能,得到下述目标函数:
 (8)
(8)
式中,![]() 是过载响应上升时间,
是过载响应上升时间,![]() 是过载响应的超调量,
是过载响应的超调量,![]() 为过载响应稳态误差,
为过载响应稳态误差,![]() 分别为阻尼回路幅裕度、幅裕度期望值、阻尼回路相裕度、相裕度期望值、阻尼回路穿越频率、阻尼回路穿越频率最大允许值、加速度回路幅裕度、幅裕度期望值、加速度回路相裕度、相裕度期望值,
分别为阻尼回路幅裕度、幅裕度期望值、阻尼回路相裕度、相裕度期望值、阻尼回路穿越频率、阻尼回路穿越频率最大允许值、加速度回路幅裕度、幅裕度期望值、加速度回路相裕度、相裕度期望值,![]() 、
、![]() 分别最大侧向角速度、最大舵偏角、最大舵偏角速度及分别对应的指标值,
分别最大侧向角速度、最大舵偏角、最大舵偏角速度及分别对应的指标值,![]() 是加权系数,可进行适当调整。
是加权系数,可进行适当调整。
仿真验证
以某一特征点为例,分别采用PSO和PSO-GA完成对导弹侧向稳定控制回路控制器参数的自化设计。
算法初始化
算法迭代次数![]() :120;种群规模:30;粒子位置上下边界值
:120;种群规模:30;粒子位置上下边界值![]() ,
,![]() ;粒子飞翔速度上界
;粒子飞翔速度上界![]() 。目标函数权重值:
。目标函数权重值:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;裕度要求:
;裕度要求:![]() 、
、![]() ;
; ![]() 、
、![]() ,遗传交叉概率
,遗传交叉概率![]() 。表1为该特征点参数情况:
。表1为该特征点参数情况:
特征点参数
序号 | | | | | | | | | |
| | 2.49 | 258.7446 | -203.0137 | 0.5850 | 0.0087 | 612.15 | 123638.8 | 1.94 | 9.7423 |
特征点定点设计仿真结果
表2为在PSO算法和PSO-GA算法下该特征点控制参数自动寻优设计结果。
两种算法的控制参数优化结果
序号 | 算法 | | | |
| | PSO | 11.517465 | 0.73831717 | 0.026537256 |
PSO-GA | 16.863501 | 0.69685713 | 0.024 |
在对该型导弹所选取特征点的定点设计中,PSO算法在某些特征点下出现最多的寻了4次才成功的情况,而PSO-GA算法均一次性成功。
两种算法的设计结果比较
序号 | 算法 | 幅值裕度(dB) | 相裕度(°) | 穿越频率(rad/s) | 上升时间 (s) | 超调量 (%) | 侧向角速度最大值(°/s) | 舵偏角速度最大值(°/s) |
| | PSO | 10.2344 | 58.6538 | 6.7085 | 0.2330 | 10.0004 | 97.3482 | 194.4088 |
PSO-GA | 8.9423 | 59.8023 | 7.0947 | 0.2160 | 10.0001 | 107.4536 | 205.7907 |
从表3可知,标准PSO与PSO-GA算法参数寻优结果满足设计指标要求。图2为单位阶跃指令下过载响应曲线。

单位阶跃响应曲线
六自由度仿真验证
为验证PSO算法和PSO-GA算法下自动设计得到的结果在导弹六自由度中同样适用,将设计结果带入到导弹六自由度模型中进行仿真,并与传统设计的仿真结果进行比较。
从图3可以看出,采用PSO算法和PSO-GA算法自动化寻优结果在六自由度仿真中的性能与传统人工设计结果相当,控制效果良好,可直接用于导弹稳定控制回路设计。

指令-过载响应曲线
结语
PSO算法和PSO-GA算法自动设计结果满足指标要求,在导弹六自由度中进行了仿真验证,控制效果良好,与传统设计结果相当,证实了本文算法在导弹侧向稳定控制回路设计中的可行性,能有效实现导弹稳定控制系统参数的自动化设计,具有一定的工程应用价值。
参考文献
[1] 张民,陈欣,陆宇平.基于改进PSO算法的导弹控制参数优化.南京航空航天大学学报,2009.
[2] 沈永福,李呈良,邓方林.基于改进遗传算法的导弹高度控制回路自动化设计.弹箭与制导学报,2002.
[3] 邱亚男,王建琦,贾晓洪.基于PSO算法的自动驾驶仪控制参数设计.航天控制,2009.