沈阳航空航天大学
摘要;化学及工业制备的效率和纯度往往受到多种影响因子的干扰,在这种条件下对于最优解的选取和研究就显得尤为重要,本文以C4烯烃的催化制备为例,分析环境温度和催化剂类型对于反应的影响,综合考虑催化剂中各种成分浓度和反应副产物,建立了乙醇偶合催化制备C4烯烃实验的多元非线性回归拟合模型,该模型可用于计算在多种影响因素共同作用下反应的相关参数,并预测出相关反应条件的最优解。
首先对已知的实验数据进行分析处理,考虑催化剂成分参数和环境温度的影响,建立多元非线性回归拟合方程,并对自变量与因变量的相关性进行讨论分析,得出最终回归方程系数的同时发现了乙醇在反应过程中产生的其他副产物浓度会随时间的变化由升高变为降低。然后基于灰色关联分析模型,研究了各个变量与乙醇转化率和C4烯烃选择率之间的关联度。基于以上分析中得出的相关性结论,分别求出4个催化剂参数变量和温度与C4烯烃收率之间的关系方程,然后运用构造函数的方法建立整体构造函数模型,基于XGBoost回归预测算法对建立的构造函数进行了五折交叉验证,最终求出反应参数的最优解。
综上所述,本文综合分析了在多种影响因子的情况下乙醇偶合催化制备C4烯烃反应的反应过程,得到了有效预测和分析反应现象以及研究反应影响因素的方法,并且该方法还可以通过排列组合的方法迭代出反应所需的最优解参数,具有较好的准确性和适应性。
关键词:多元非线性回归,灰色关联分析,XGBoost回归预测,最优解
一、问题重述
1.1 背景
C4烯烃目前广泛的被应用在化工产品和医药科学等领域,目前C4烯烃的来源基本分为两种,一是通过高温的催化裂化,这种方法制备的C4烯烃大约占总产品的52.5℅;二是通过乙烯裂解的方式[1]。而这两种方式对传统的化石能源都有很高的依赖性,不是长远之计,所以利用乙醇偶合制备C4烯烃可能成为烯烃生产的未来趋势,拥有巨大的开发前景和经济效益(图1.1)。

图1.1 各国乙醇产量占比图[2]
而在催化反应过程中总会因受到多种因素的影响而导致乙醇转化率偏低,或者C4烯烃的纯度较差,而大量的实验又会导致财力人力的浪费,所以利用数学分析求出多影响因素下催化反应的最优解就成了大家普遍研究的方向。
二、实验数据及影响因素选取
针对四组变量选取四组催化剂实验数据如下:
催化剂组合 | 温度 | 乙醇转化率(%) | 乙烯选择性(%) | C4烯烃选择性(%) | 乙醛选择性(%) | 碳数为4-12脂肪醇选择性(%) | 其他生成物的选择性(%) |
200mg 1wt%Co/SiO2- 200mg HAP-乙醇浓度1.68ml/min | 250 | 2.07 | 1.17 | 34.05 | 2.41 | 52.59 | 9.78 |
300 | 14.97 | 3.02 | 46.94 | 4.71 | 35.16 | 9.17 | |
350 | 36.80 | 12.46 | 47.21 | 18.66 | 9.22 | 10.76 | |
200mg 2wt%Co/SiO2- 200mg HAP-乙醇浓度1.68ml/min | 250 | 4.60 | 0.61 | 18.07 | 0.94 | 72.99 | 7.39 |
300 | 38.92 | 0.85 | 19.6 | 2.21 | 67.5 | 9.84 | |
350 | 67.88 | 2.76 | 39.1 | 4.2 | 36.92 | 15.15 | |
200mg 1wt%Co/SiO2- 200mg HAP-乙醇浓度0.9ml/min | 250 | 9.7 | 0.13 | 5.5 | 1.23 | 85.09 | 4.08 |
300 | 29.3 | 0.71 | 17.01 | 3.63 | 66.9 | 8.57 | |
350 | 48.9 | 2.85 | 36.85 | 7.23 | 38.29 | 11.27 |
三、模型的建立与求解
3.1 研究乙醇转化率、C4 烯烃的选择性与温度的关系
为直观的展现出反应过程中温度与对应的C4烯烃选择性、乙醇转化率之间的变化关系,我们对上述催化剂组合,分别制定了相对应的多元非线性回归曲线图,以及对应变量的变化折线图。
表3.1 不同催化剂的分析图像
催化剂 | 多元非线性回归曲面图 | 对应变量变化折线图 |
200mg 1wt%Co/SiO2- 200mg HAP-乙醇浓度1.68ml/min | | |
200mg 2wt%Co/SiO2- 200mg HAP-乙醇浓度1.68ml/min | | |
200mg 1wt%Co/SiO2- 200mg HAP-乙醇浓度0.9ml/min | | |
为了确定反应温度与C4烯烃选择性、乙醇转化率之间的变化关系,我们选择C4烯烃选择性或者乙醇转化率作为因变量,其他变量作为自变量,建立多元非线性回归预测模型[3],模型为:

(1)

式中 y是C4烯烃选择性,x1是乙醇转化率,x2是温度。
分析给定温度下实验中不同时间的测试结果,我们需要将自变量与因变量的相关性分开讨论,即强相关性和弱相关性。为了明显的展示变量之间的相关性,绘制6*6的矩阵热力图[4](图3.1)和在不同时间下因变量的变化条形图(图3.2)。

图3.1 相关性矩阵热力图
从上图中我们发现,大部分变量随时间成单调性变化,但有几种因变量随时间并不是单调变化的,例如其他生成物的选择性随时间的变化先升高而后又降低。
根据相关实验数据对建立的多元非线性回归预测模型求解,求出参数β0,β1,β2,β3。(表3.2)
表3.2 预测模型参数值求解
| β0 | β1 | β2 | β3 |
催化组1 | 133.1316856 | 1.995744022 | 4.352811957 | -0.027619333 |
催化组2 | 295.754128 | 1.526991293 | -4.184980173 | 0.074950596 |
催化组3 | 202.1638237 | 3.820419537 | 0.740181489 | -0.052507635 |
实验数据中其他生成物的选择性随时间的变化先升高而后又降低的现象是由于反应前期会有其他副产物的出现,但随着时间的变化,反应越来越充分,其他生成物含量逐步降低,所以导致因变量不随时间单调性变化[5]。
3.2 不同催化剂组合及温度对乙醇转化率以及 C4 烯烃选择性大小的影响的探究
针对实验数据建立灰色关联分析模型[6],具体建立步骤如下:
步骤1:确立母序列
在此需要分别将四种催化剂种类以及温度与乙醇转化率比较计算其关联程度,故母序列为乙醇转化率。
步骤2:无量纲化处理
在此采用均值化法,及将各个序列的实验数据与整条序列的均值作比值,进行数据的无量纲化处理。
步骤3:计算每个子序列中各项参数与母序列对应参数的关联系数
根据公式:

(2)

其中 表示第i个子序列的第k个参数与母序列(即0序列)的第k个参数的关联系数。
表示第i个子序列的第k个参数与母序列(即0序列)的第k个参数的关联系数。
步骤4:计算关联度
利用MATLAB求解公式计算关联度:

(3)
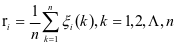
根据关联度计算结果我们发现:
1、HAP浓度与乙醇转化率之间的关联度最大,为0.7415;即乙醇转化率受HAP浓度的影响最大。
2、温度与C4烯烃选择性之间的关联度最大,为0.7745;即C4烯烃选择性受温度的影响最大。
3.3 选择催化剂组合与温度
根据前文我们得出的相关性结论,将温度、Co负载量、HAP含量、Co/SiO2和HAP装料比,以及乙醇的倒入速度这四个变量做自变量,以C4烯烃收率做因变量,分别求出五个变量与C4烯烃收率之间的相关系数(表3.3)。
表3.3 各自变量与因变量之间的拟合系数
| 常数项 | 一次项系数 | 二次项系数 |
温度 | 0.108432099 | -57.50718308 | 7667.014611 |
co | -0.00378755 | 5.506961048 | 118.9345322 |
co/sio2 | -33.05489722 | 156.0976044 | 500.7508501 |
HAP | -0.003628597 | 5.467362878 | 120.5086699 |
乙醇浓度 | -444.3831475 | 671.9813269 | 708.4637644 |
则根据表格可得出相关函数关系:

(4)

然后在将得出的五个函数关系构造成为一个总的函数表达式,最终建立构造函数关系的模型[7]:

(5)

我们选择用XGBoost算法求解所建立的构造函数,通过五折交叉验证的方式按着一定步长进行排列组合最终求出最优解。其中XGBoost集成算法公式可表示为:

(6)

设目标函数为:

(7)
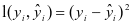
则可利用下列函数[8]求出最优解:

(8)

最终得出最优解(表3.4):
表3.4 XGBoost模拟预测结果
C4烯烃收率 | 温度 | HAP(mg) | Co负载量 | 乙醇浓度 | Co/SiO2 |
4452.064941 | 400 | 200 | 200 | 0.9 | 1 |
4309.157715 | 450 | 200 | 200 | 0.9 | 1 |
4309.157715 | 565 | 197 | 34 | 0.96 | 1.3 |
4309.157715 | 524 | 285 | 293 | 0.72 | 1 |
4309.157715 | 536 | 292 | 323 | 1.2 | 0.9 |
4309.157715 | 534 | 273 | 326 | 0.75 | 0.9 |
根据预测结果我们发现在温度为400℃,催化剂中HAP200mg,Co负载量200,乙醇浓度0.9ml/min,Co/SiO2为1时C4烯烃收率最高,为4452.064941。
四、模型的推广
本文中所建立的三种模型适合对于包含多个自变量问题的讨论和分析。例如,在疫情防控工作中对于病毒感染率的影响因素有很多种,包括地区人流量、政府宣传力度、交通、医疗情况等,当讨论这些影响因素中一种或几种与病毒感染率的关系和相关性,以及研究疫情防控工作最优化落实问题时都可以运用本文中所使用的模型。
参考文献
[1]吕绍沛. 乙醇偶合制备丁醇及C_4烯烃[D].大连理工大学,2018.
[2]张扬健,向威达,周涛,雷家骕.我国燃料乙醇发展现状和趋势分析[J].中国能源,2009,31(01):31-33+42.
[3]董大校.基于MATLAB的多元非线性回归模型[J].云南师范大学学报(自然科学版),2009,29(02):45-48.
[4]纪连恩,高芳,黄凯鸿,陈宗艳.面向多主体的大学课程成绩相关性可视探索与分析[J].计算机辅助设计与图形学学报,2018,30(01):44-56.
[5]江思祺. 生物质乙醇制备异丁烯工艺路线的探究[D].北京化工大学,2019.
[6]曹明霞. 灰色关联分析模型及其应用的研究[D].南京航空航天大学,2007.
[7]潘琦,路线.构造法在数学分析中的应用[J].吉林工程技术师范学院学报,2017,33(05):93-96.
[8]赵征,冯事成,宋梅雯,胡莉,陆莎.基于XGBoost的航空器动态滑行时间预测方法研究[J/OL].航空工程进展:1-10[2021-09-12].
课题名称及编号:出版/文献/信息传播/知识产权事务费21312007306

1