浅析表面修饰调控单层ZnS电子结构和光学性质

浅析表面修饰调控单层 ZnS电子结构和光学性质

肖建峰

江苏金陵机械制造总厂 江苏南京 21000

摘要：文章以单层ZnS为研究对象，在对F修饰以及H修饰相关结构进行建立的基础上，利用DFT法对不同二维材料对应稳定性和晶体结构进行了计算，同时分析了表面修饰给ZnS光学性质、内部电子结构所产生影响，供相关人员参考。

关键词：光学性质；电子结构；单层ZnS；表面修饰

前言：作为具有直接宽带隙特征的半导体，ZnS在电致发光、荧光效应还有红外透过性等方面均有极为突出的表现，加之ZnS在室温条件下较为稳定，现已被广泛用于对短波发光器以及光传感器进行制造的领域。但现有研究普遍集中在三维ZnS方面，二维ZnS鲜有涉及，鉴于此，本文选择以密度泛函理论为依据，对F、H给ZnS所产生影响进行研究，希望能为日后制备优质二维材料的工作提供理论依据。

1建立模型

单层ZnS的结构为六元环，对称群是 ，出于弱化相邻各层间所存在范德华力影响的考虑，研究人员选择沿轴方向对真空层进行设置^[1]。单个分子及原子所发生吸附反应，可被视为杂质引入，经过表面修饰的ZnS，其性质还有内部结构均与初始ZnS不同。

本项目中研究人员决定分别对氟基、氢基进行修饰，并利用二者对ZnS进行半表面修饰。在同时对F、H进行修饰时，若F位于S侧且H位于Zn侧，则将其记成hH-ZnS-hF，若F位于Zn侧且H位于S侧，则将其记成hF-ZnS-hH。对各项数值进行计算所使用软件为CASTEP，综合应用PBE、GGA等算法对电子间所存在关联能进行处理，将平面波阶段能设为500eV，收敛精度为 ，同时保证各原子受力在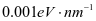 以下，对应收敛精度为^[2]。

2结果分析

2.1电子结构

对二维材料进行研究的切入点，通常为实验可行性以及稳定性，除特殊情况外，均可以声子谱所呈现出软化程度为依据，对结构是否稳定进行判断。通过计算可知，fH-ZnS以及ZnS不存在虚频，剩余体系则在G点周围存在微弱虚频，可忽略不计，这说明本项目所选用材料在动力学稳定性方面的表现可达到预期。

对修饰所得ZnS对应能带图进行分析可知，ZnS导带底、价带顶均处于G点处，这表明ZnS的本质是直接带隙的半导体，对应计算能隙取值是2.635eV。对其进行修饰后，可使能带结果出现明显变化，hH-ZnS-hF、hF-ZnS-hH对应价带顶均从最初的G点更改为K点，这表示半导体从早期的直接带隙更改为间接带隙，同时fH-ZnS对应能隙有所增大。剩余修饰体系仍属于直接带隙，但能隙均有所减小。此外，修饰所得ZnS，其价带顶所具有局域化程度较初始ZnS更强，通过分析可知，F原子以及H原子具有极强的电负性，由于上述原子的存在，使得S、Zn对应轨道电子逐渐向F、H偏移，二者所表现出电负性的差别越明显，其离子属性自然越强，此时，电子态的局域化程度自然更突出。

要想对各原子给对应轨道所作出贡献加以明确，通常需要先对电子分波态的真实密度进行计算。通过分析可知，ZnS价带所包含电子以S-3p为主，导带所包含电子则以Zn-4s为主，需要明确的是，虽然Zn-3d给价带所产生影响往往可忽略不计，但Zn-3d具有和S-3p大致相同的变化趋势，使得两个轨道间产生明显的杂化效应。Zn-4s和S-3s同样存在杂化效应。在利用F、H对ZnS进行修饰时，原子对应分波态密度通常会发生大幅波动，具体表现为价带顶周围电子分布较修饰前更强。另外，F-2p、H-1s所处区域以浅处能级为主，对ZnS进行修饰后，其价带顶周围将出现明显的局域化情况，促使上价带电子朝低能方向持续移动，使得电子态呈现出显著的低能化特征。此外，导带定周围能量的分布情况同样存在一定程度的变化，其中，fH-ZnS、ZnS以及hF-ZnS-hH均出现了由Zn-4s所构成微弱峰值，而fH-ZnS还有hH-ZnS-hF的存在，使导带顶周围出现了由F-2p、S-3p所构成强烈峰值，相应地，导带底所分布量子态有所增多，这也是其具有较初始ZnS更为理想的吸光效果的原因所在。

研究表明，载流子质量和迁移速度间的关系多为负相关，即：空穴、光生电子质量越小，对应迁移速度越大。对载流子质量进行计算的公式如下：

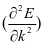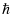在上述公式中， 的单位是 ，其中，a所描述对象为晶格常数，即 。 的取值为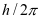 。由此可见，载流子质量往往由导带底、价带顶对应二次微分所决定。考虑到空穴多处于价带顶周围，而电子在导带底周围较为常见，通常只需对二者对应二阶导数进行计算，便可获得空穴、电子质量的相关数值。计算所得结果见表1：

表 1 载流子质量计算结果

在该表中，m_h所描述对象为空穴质量。m_e所描述对象为光生电子质量。而m₀所描述对象为电子质量。对表1所记录数据进行分析可知，ZnS对应m_h取值通常较m_e略小，这表示其电子迁移率较空穴更小，符合p型半导体相关特点。而修饰所得ZnS，其价带顶对应色散曲线较修饰前更为平滑，表明E、k对应二阶导数较小，相应地，其质量自然有所增加，简单来说，就是修饰所得半导体对应空穴质量较初始半导体更大。综上，对ZnS进行修饰，可使其空穴质量有所增加，与n型半导体相关特点相符，同时不同修饰体系对应m_h还有m_e数值间存在显著差异，表明修饰期间，ZnS空穴、光生电子对应迁移速率均发生了明显变化，载流子分离程度加剧，空穴和电子所具有复合率随之降低。

2.2光学性质

出于对初始ZnS和修饰后ZnS所表现出光学性质进行分析的考虑，研究人员决定先对介电函数进行计算，再结合直接跃迁、色散关系，对其吸收系数和其他光学常数进行推导，相关表达式如下：

在上述表达式中，ω所描述对象为频率。ε₁(ω)所描述对象为实部。ε₂(ω)所描述对象为虚部。对吸收系数、光子能量间的关系进行分析可知，单层ZnS对应吸收边取值在1.7eV左右，未达到能隙值，由此可见，ZnS为重电子、轻空穴半导体，其空穴具有较电子更高的迁移率，使得空穴复合速率显著降低，可被用来对小能隙能量所携带光子进行吸收。经过修饰所得ZnS各吸收边与能隙值相符，而出现上述现象的原因，主要是吸收边极易被光学带隙所影响，只有最大程度缩小能隙值、光子能量间所存在差距，才能获得相应的耦合效应，确保电子可在导带、价带之间合理跃迁。

综上，F修饰及H修饰均会促使ZnS对应吸收边出现蓝移情况，其中，F修饰会直接影响ZnS吸收值，使其在2.5eV以下的吸收值较修饰前略低，同时使2.5eV~4eV间的吸收值显著增加，利用其吸收短中波紫外线，通常可取得较为理想的效果。而H修饰给ZnS所产生影响，主要是使其整体吸收效果下降，有关人员应对此有所了解。

结论：研究人员利用DFT法对ZnS进行了计算，结果表明作为准平面的单层ZnS，在经过相应的修饰后，结构转变成了褶皱六元环，同时F、H在吸附期间均发生了放热反应，这表示修饰所得ZnS可通过实验进行合成，其化学稳定性基本能够达到预期。对电子结构进行分析可知，单层ZnS为直接带隙，利用H对其进行修饰，会使其能隙有所增大，从而变成间接带隙。而ZnS所表现出光学性质传递了以下信息：价带顶所发生空穴复合反应较为滞后，使得浅处能级在带间进行合理跃迁成为可能，ZnS对应吸收边较能隙值略小，表示修饰期间其吸收边存在蓝移情况，这一改变赋予ZnS较以往更为理想的吸收性能，应引起重视。

参考文献：

[1]郭佳,张鹏程,刘春景,等.表面修饰调控锑烯SbX(X=-CN,-NC)的电子结构与光学性质[J].华中师范大学学报：自然科学版,2020,54(6):8.
[2]王骏齐,张衍敏,陈天弟,等.不同浓度Ag掺杂ZnS的电子结构及光学性质的第一性原理研究[J].材料导报,2019,33(A01):4.