点到平面距离的几种证明方法

点到平面距离的几种证明方法

周明旺

连云港师范高等专科学校 数学与信息工程学院 ,江苏 连云港 222006

摘要：分别利用点线面之间的关系、多元函数求极值的相关知识，从四个不同视角给出点到平面距离的不同证明方法，以培养学生几何空间观念以及提高分析问题、解决问题并综合应用知识的能力。

关键词：解析几何；平面；距离

中图分类号：Ｏ182 文献标志码：A

基金项目：国家自然科学基金资助项目（10771182）

1．引言

解析几何是师范教育专业的一门重要的基础课程，点到平面的距离是解析几何的重要研究内容之一，也是非师范专业高等数学的重要教学内容之一。寻求点到平面的距离公式的来龙去脉不仅可以激发学生学习数学的兴趣，而且也是有效培养学生思维发散的有效途径，进一步培养学生几何空间观念，提高分析问题、解决问题并综合应用知识的能力。

2．预备知识

引理1 向量 在向量上 的射影 .

定义1 如果自点 到平面 引垂线，其垂足为 ，那么向量 在平面 的单位法向量 上的射影叫做点 与平面 间的离差，记作 。

引理2 点 与平面 间的离差是

，其中 是原点到到平面 的距离。

引理3 点 到平面 间的距离 等于点与平面间离差 的绝对值，即 。

3．主要结果

以下就不同的视角证明点到平面的距离公式。

定理 点 到平面 间的距离为 。

证法1 将平面 的左右两端同乘以法式化因子

其中的正负号选取一个，使它满足 ，

得到平面 的法式方程 ，则点 与平面 间的离差为 ，由引理3，点 到平面 的距离为 。

证法2 过点 引平面 的垂线，垂足为 ，则 为点 与平面 间的距离。

平面 的法向量为 ，过点 且以 为方向向量的直线 的参数方程为 ，直线 与平面 垂直相交。把直线 的参数方程代入平面 方程得 ，求得参数 ，代入直线 的参数方程，求得直线 与平面 的交点坐标为

由两点间的距离公式求得 ，即点 到平面 的距离为 。

证法3 平面上的任意点 ，则 在平面 的法向量 上的射影的绝对值即为点 与平面 间的距离。

在平面 上任取点 ，易知 ，

，平面 的法向量 。则 与平面 间的距离为

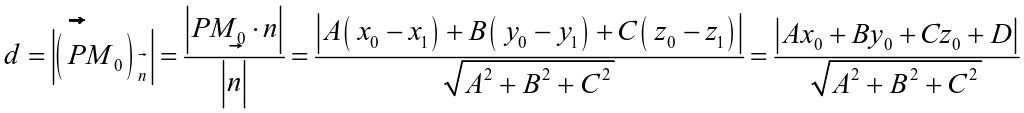
证法4 利用多元函数条件极值的拉格郎日乘数法证明。

点 与平面 间的距离是平面 上的点与点 之间距离的最小值。

设平面 上任意点 ，构造目标函数 ，限制条件为

，其中 。

设辅助函数

令

，解出 ，代入

，得

从而点 与平面 间的距离为：

特别地，对坐标面 上的点 ，则点 与平面 间的距离 恰是平面解析几何中的点 到直线 的距离公式。

4．结束语

厘清点、线、面之间的位置关系与对应的几何量之间的数量关系是空间解析几何学习的关键。从以上证明点到平面的距离的不同方法可以看出思路虽然有差异，却是殊途同归，这正是数学的美妙之处，对于培养学生思维发散性，加深对几何空间观念的理解、提高分析问题、解决问题并综合应用知识的能力意义重大。

作者简介：周明旺(1969-)，男，江苏赣榆人，副教授，硕士，主要从事量子群研究与几何类课程的教育教学。

参考文献：

[1]吕林根,许子道.解析几何[M].第5版.北京:高等教育出版社,2019:73-74

[2]同济大学数学系.高等数学:上册[M].第4版.北京:高等教育出版社.1996:417-423

[3]同济大学数学系.高等数学:下册[M].第4版.北京:高等教育出版社.1996:61-71