山东协和学院 山东 济南 250107
摘要:为了以最少的原材料满足结构强度、刚度要求,利用ANSYS对一个横截面为矩形的钢梁进行了优化设计,得到了弯矩、最大挠度和最大应力等计算结果。通过分析比较有限元计算结果与理论结果,验证了有限元计算结果的正确性;并对比分析了优化设计截面与矩形截面的计算结果,证明了优化截面的优势,为改善梁截面形状优化设计提供了参考。
关键词:优化设计;ANSYS;矩形截面梁
目前在工程领域,建筑的安全与投资的效益是评价建筑是否合理的两个主要方面,即如何保证建筑的安全生产,又能最大程度的减少建筑的造价。结构优化设计就是从这一思考方向向前发展的,结构的优化是在众多的设计方案中求出最为经济的截面尺寸,使设计既满足强度和构造要求又最为经济合理的设计方案[1]。梁在土木工程中作为重要的基础构件之一,应用广泛,为土木工程专业大学生主要学习构件,故本文选取了梁为研究对象,探索截面的优化,在保证安全的前提下,减少材料的使用。
随着计算机的发展,ANSYS作为一种强大的有限元力学分析软件,成为结构设计分析中常用的有限元分析软件之一。利用ANSYS模拟建筑结构受力情况进行数值分析,能够为设计人员在结构优化方面大大减少繁冗的计算过程,方便设计人员对比分析不同的优化设计方案,为设计人员赢得了宝贵的时间。ANSYS与大学生建筑类专业密切相关,结合ANSYS对梁构件进行横截面优化设计,可以辅助大学生理解、掌握力学相关专业知识,有利于提高大学生综合素质,强化专业能力,利于在后续工作中做到游刃有余。
一、梁计算模型
本文分析计算模型为等截面外伸梁,原截面形状为矩形,材料为钢。原梁矩形截面尺寸、材料弹性常数如表1所示;梁的支座及加载情况如图1所示,采用对称加载,中部为纯弯曲段。
在进行截面优化设计时,根据构造要求和强度要求进行设计,目标为减小梁所受的最大正应力及挠度,从而提高梁的承载力与刚度。结合《材料力学》中合理选取截面形状提高梁强度与刚度的力学知识,在优化截面时,采了尽可能使横截面面积分布在距中性轴较远的地方的设计思路,达到优化截面的目的。
表1 原截面梁的有关参数
宽度b | 高度h | 跨度l | 支座与作用点距离a | 弹性模量E | 泊松比μ | 最大弯矩M |
20mm | 40mm | 700mm | 125mm | 206GPa | 0.26 | 31250N·mm |

图1 梁支座与加载位置
二、 矩形外伸梁截面分析
两外力在该梁中关于中心对称,在梁荷载中间为纯弯曲,且存在最大弯矩,最大的正应力位于该段梁横截面上距中性轴最远处。原矩形截面时梁理论计算分析结果如下:
1.最大正应力


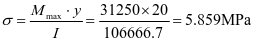
2.最大挠度

三、外伸梁优化截面分析
1.优化的横截面形状
优化的梁截面形状如图2所示。根据构造要求,圆形内壁与矩形边界连接的最薄处在承受力及力偶作用时,易发生弯折导致结构破坏,所以在截取圆形截面时不应半径过大,要保证该薄弱处满足一定的强度、刚度等承载力要求。过矩形中心剪切半径为10mm的圆形,使截面尽量远离中性轴,降低梁截面所承受的最大弯矩与应力,从而达到提高梁的截面有效利用率的效果。
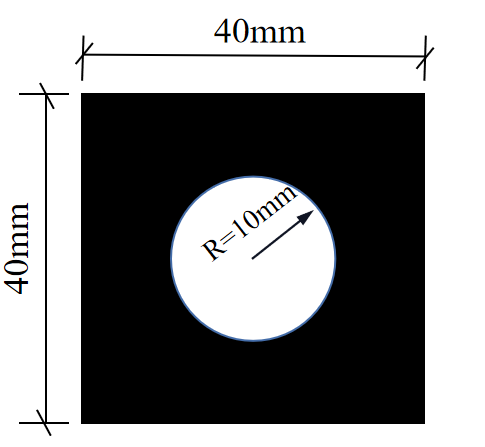
图2 优化截面形状
2.优化截面理论分析
(1)最大正应力
在计算梁截面的截面惯性矩时,圆形截面与矩形截面有共同的中合轴,可直接用矩形的截面惯性矩减去圆形的截面惯性矩得到优化后的梁截面惯性矩。



(2)最大挠度

3.优化截面ANSYS数值分析
(1)有限元模型
利用ANSYS软件对优化后的梁进行有限元分析,选用的单元为BEAM188,设置单元长度为5mm,与原矩形截面梁加载条件相同,进行了网格划分后,建立的有限元分析模型如图3所示:

图3 ANSYS有限元分析模型
(2)有限元分析结果
对受两个集中力作用的外伸梁构件进行了有限元分析,最大正应力为3.04MPa,最大挠度为0.03mm。
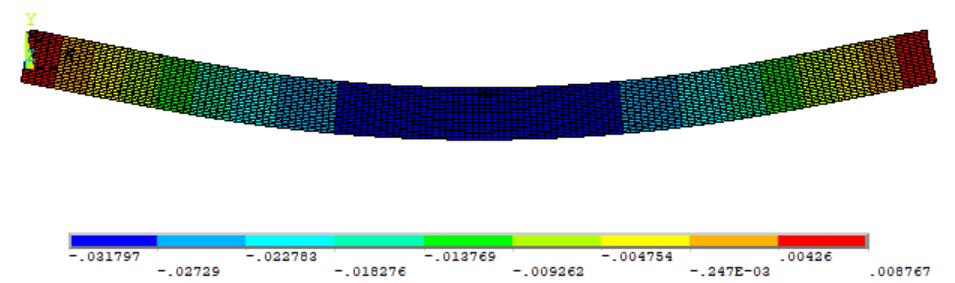
图4 ANSYS挠度云图

图5 ANSYS应力云图
(3)与理论分析对比
对受两个集中力作用的外伸梁构件优化截面进行了有限元分析,与理论值相比应力有一定的增大,挠度接近,具体如表1所示。ANSYS模型建立时单元的大小个数对实验结果具有一定影响,挠度与应力大小变化在误差范围内,所以优化结果是合理的。
有限元优化设计能够为工程技术人员提供结构概念性优化设计方法,其分析计算过程不再依赖人工结构分析,减少了结构设计过程中不断重复设计所消耗的时间,缩短了设计开发的周期,而且精度也大大提高,从而提高产品质量,增强企业的竞争力[2]。
四、优化截面与矩形截面结果对比
通过优化截面与矩形截面分析,如表2可得出在该优化截面下,与原试件矩形截面相比,WZ与截面面积A之比提高了24%;最大挠度由减小了50%;最大正应力减小了49%左右。优化后的梁截面利用率明显提高且所承受的最大正应力与挠度明显降低,承载力提高。
表2 优化对比分析
梁的截面形状 | W/A (mm) | 最大正应力(MPa) | 最大挠度 (mm) |
矩形截面梁 | 6.67 | 5.859 | 0.06 |
优化截面梁理论分析 | 8.28 | 2.94 | 0.03 |
优化截面ANSYS分析 | 8.28 | 3.04 | 0.03 |
理论/ANSYS分析 矩形与优化截面结果对比(%) | 24.14/24.14 | -49.82/-48.11 | -50.00/-50.00 |
该实验以等截面外伸钢梁为研究对象,分别从构件强度、位移、构造方面对结构进行设计,考虑矩形横截面外伸梁的受力特征进行形状优化,以等截面钢梁造价为优化目标,通过大型通用有限元软件ANSYS对优化截面梁建立模型并分析计算。
1.运用了有限元法得到了梁最大应力和最大位移等计算结果,与理论值进行对比,从而可知结果与理论值非常接近,说明了有限元优化结果是有理论基础的。
2.钢梁设计在满足强度和构造条件下,可有多种截面尺寸的组合,本文优化的截面与矩形截面相比,挠度、应力降低,承载力提高,对于梁的工程应用有极大的促进作用。
参考文献:
[1]龙华.钢筋混凝土矩形梁正截面优化设计[J].水利规划与设计,2011(04):58-59
[2]张黎明,张长平.基于ANSYS的变截面悬臂梁形状优化设计[J].牡丹江大学学报,2009,18(09):111-115
基金项目:2021年山东协和学院实验室开放项目《基于ANSYS的矩形钢梁截面形状的优化设计》(项目编号:2021SYKF30)