毫米波雷达汽车盲区监测系统波形选择

毫米波雷达汽车盲区监测系统波形选择

熊递恩 重庆机电职业技术大学 ，重庆 400054

摘 要：为了提高毫米波盲区监测系统性能，选择一种适合雷达盲区监测系统的体制，文章提出一种多频移键控调制方式。首先，分析其测速测距原理以及频域特性。然后借助MATLAB软件，根据模糊函数图，与常规线性调频连续波进行对比，仿真结果显示，多频移键控调制波形具有更高的距离和速度分辨能力，而且能够解决线性调制频谱匹配问题，同时满足测量多目标、无虚假目标。最后实验室测试以及室外实时路测，采集数据分析，实现目标距离的测量在2m至60m范围内测量，其误差在1m以内，误报率为2.436%，漏警率为2.79%，系统平均误差为4.904%，并且可同时探测多个目标。

关键词：汽车盲区监测；多频移键控调制；模糊函数

中图分类号：TN958 文献标志码：A

1 引言

近年来，我国汽车保有量逐渐上升，交通事故的死亡人数逐年增加^[1]。奔驰汽车公司对各类交通事故的研究表明：若驾驶员能够提早1s意识到事故危险并采取相应的正确措施，则绝大多数的交通事故都可以避免，因此汽车防撞雷达系统运用而生^[2]。美、日、德、瑞典等国对汽车防撞雷达技术研究较早，已有产品部分产品已安装在高档车辆上。国内对汽车雷达的研究起步较晚^[3]，主要有微系统研究所、各汽车公司、高校和部分创新性企业等机构。毫米波传感器因受天气影响小，精准度高，抗干扰能力强、探测距离远，穿透能力强等优势被广泛应用在车载雷达上^[4-5]。

道路是一个复杂环境，需要设计一种具有较好的距离分辨率和速度分辨率的汽车防撞雷达的波形。线性调频波（LFMCW）调制具有计算简单，分辨率较好的优点，但是在多目标的情况下，会出现虚假目标^[6-8]；变周期锯齿波的调制具有简单地目标匹配算法，但是采用最小耦合距离差的匹配方法可能导致多普勒频移大的目标丢失和虚假目标的产生^[9]；自适应波束控制的相控雷达，提高系统的测量范围和精度，但复杂的硬件系统和高昂的成本使其应用受限^[10]；多进制数字频率调制（MFSK）结合了频移键控（FSK）与LFMCW的优点，MFSK既解决LFMCW频谱匹配的麻烦，降低恒虚报警率，又解决FSK无法区分同速目标的困难。本文主要研究一种适合汽车防撞系统的MFSK波形，对其进行了MATLAB仿真，以及实验测试，结果表明满足测量多目标、测量时无虚假目标的要求。

2 系统测速测距原理

MFSK调制雷达实现原理是交替发射两种具有固定频差波形，并且两种频率均是线性阶梯步进，其实质是FSK与LFMCW的结合^[11]，如图1所示， 、 表示两种不同频率发射波形，其固定频率为 ，每种波形步进频率间隔为 ，频率带宽为 。

设发射N个频率步进信号,第i个信号为：

（1）

其回波信号为：

（2）

图1 MFSK调制波形

混频之后N个采样差频信号进行FFT变换和理论推导，可得距离R和速度V存在以下关系：

（3）

（4）

式中f为差频频率， 为A、B相位差，根据公式（3）（4）可知，如果知道f、 即可求得目标的距离和速度信息，而且f、 与距离R和速度V一一对应。

图2（a）LFMCW距离速度匹配

图2（b）MFSK体制速度距离匹配

根据图2可知，MFSK调制方式不存在交叉混叠，有效地解决了LFMCW调制上下扫频存在虚假目标问题。而且弥补2FSK不可以区别同速移动目标的问题，其常见调制方式的优缺点如表1所示。

表1 常见调制方式对比

3仿真分析

3.1 模糊图仿真分析

雷达系统性能的好坏直接影响工作探测指标，而模糊函数可以表示出雷达系统固有分辨率和模糊度，也可以表示出雷达采用该信号后可能到达的距离、速度测量精度和杂波抑制方面的能力，所以可以根据模糊函数定性分析雷达系统体制选择的好坏^[12-14]。模糊函数的定义为：

式中 表示两个目标的延迟时间差， 表示两个目标多普勒频移之差， 为雷达信号瞬时表达式。 表示两个目标信号回波复包络的时间-频率复合自相关函数。模糊函数的模值 给出了两个相邻目标距离-速度联合分辨能力的一种度量，如果 随 和 的增加而下降的越迅速，则两个目标就越容易分辨，也就是模糊度越小。不同雷达信号，参数的选取以及调制方式的应用均不同，生成的信号形式也各不相同。从模糊函数图的形状划分，雷达信号可分为正刀刃形、斜刀刃形、图钉形和钉床形四种类型^[15]。而且模糊函数图原点处的主瓣尖面越窄，则具有越高的距离和速度分辨能力。MATLAB仿真条件如表2所示。

表2 MFSK与LFMCW模糊函数仿真条件

图3（a） MFSK调制模糊函数

图3（b） LFMCW调制模糊函数

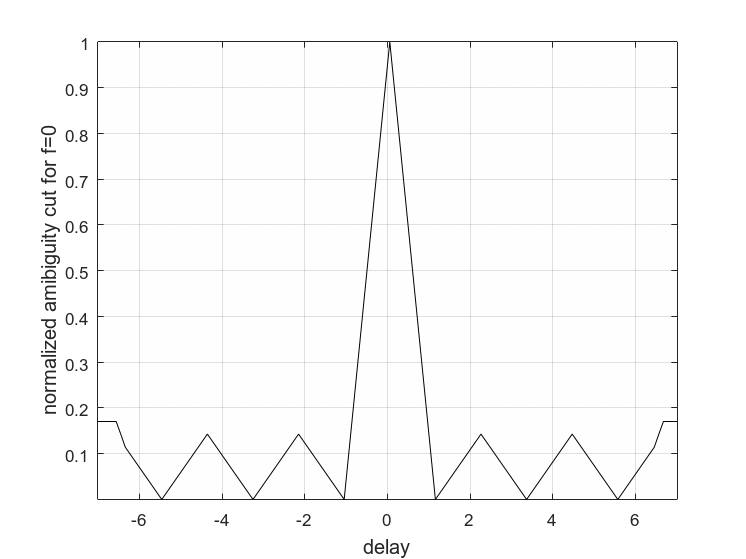
图4（a）MFSK距离模糊函数图

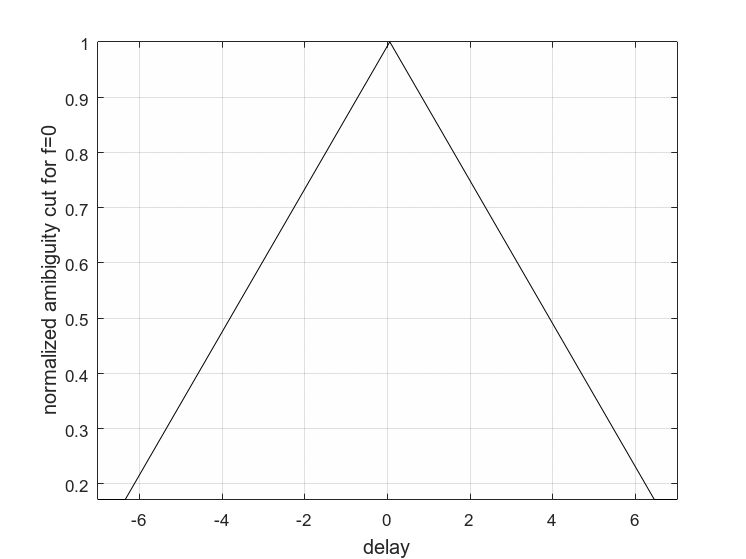
图4（b）LFMCW距离模糊函数图

从图3（a）（b）对比可以看出，在相同带宽和相同发射周期的条件下，MFSK的三维模糊函数图更接近“图钉”形状，LFMCW的三维模糊函数图是“斜刀刃”形状较，所以MFSK信号有很大的提高，MFSK优于FSK区分两个目标。从图4（a）（b）对比可以看出，MFSK距离模糊函数图原点处的主瓣尖面宽度要小于LFMCW信号主瓣宽度，所以MFSK要优于LFMCW距离分辨能力，所以本次设计采用MFSK调制。

3.2 多目标仿真分析

道路环境复杂，往往存在多目标情况，因此系统不仅需要探测出危险目标还需要有区别出多目标能力，本文就系统多目标情况进行仿真实验，其仿真条件如表3所示，为了更贴切真实路况，这里分别设定了静止目标和运动目标、相同距离不同速度目标，相同速度不同距离的目标，目标的速度距离参数如表4所示。

表3 系统仿真参数

表4 目标距离速度参数

仿真输出结果如图5所示，其中蓝色圆圈为给定数据，黑色雪花型为测量结果，横坐标为速度值，纵坐标为距离值。

图5 不同速度距离目标

统计仿真数据，结果具体误差分析如表5所示。从图5可知能够检测到所有的目标，没有目标丢失，而且均在理想目标附近，目标1和目标3对比仿真结果表明了系统分别能够检测到运动目标和静止目标，目标4和目标6对比仿真结果表明了系统能够分辨出相同速度的目标，目标1和目标2对比仿真结果表明了系统能够分辨出相同距离的目标，其距离误差在1.056m左右，速度误差在0.487m/s左右，所以MFSK调制符合要求系统假设指标。

表5 目标距离速度统计

续：

4 路测分析

本系统首先通过下位机（雷达板）对回波信号进行数据采样、预处理，然后通过SPI经过USB转SPI板将数据送到上位机（电脑）。为了保证采集数据的实时处理，上位机采用串口中断方式接收数据，通过上位机视频窗口观测目标检测情况，如图5（a）（b）（c）所示。

图5（a） 正后方有目标的路测情况

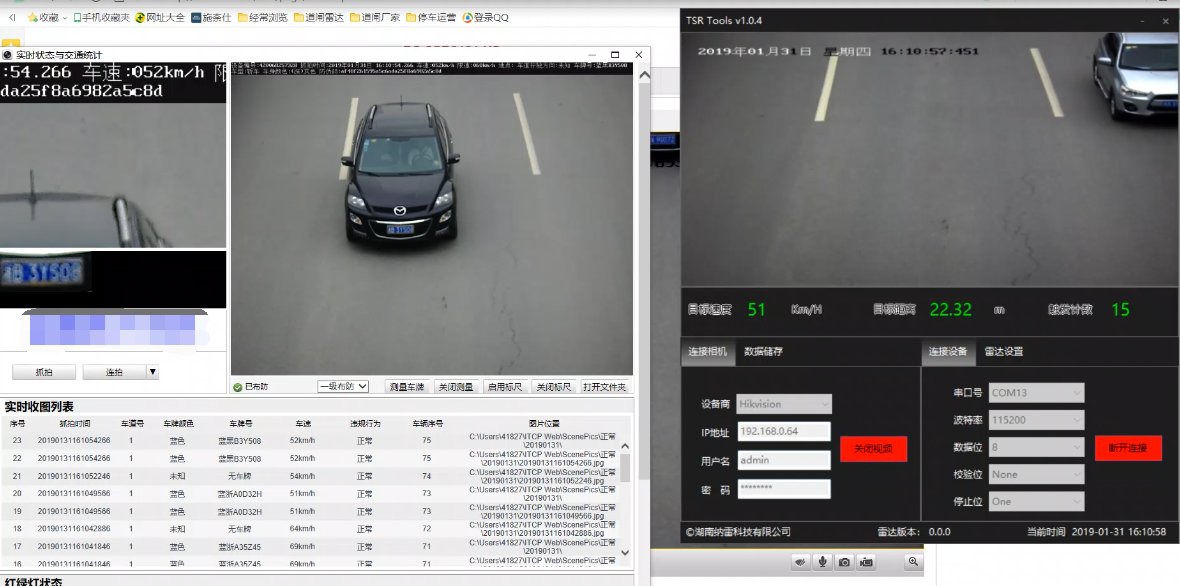
图5（b） 侧右后方有目标时的路测情况

图5（c） 侧左后方有目标时的路测情况

由图5路测情况显示结果图可知当正后方60米之内有车靠近，则别判断为存在目标，那么雷达防撞系统正确捕捉到目标，并且实时正确测出目标的距离以及此时对应的目标速度，此时在上位机的视频窗口将显示出来，如图5（a）所示，目标为黑色小轿车，当前距测试小轿车22.14米，以相对测试车速度51

靠近。从图5（b）路测情况显示结果图可知，如果车侧右后方有车行驶，不在正后方的探测范围，则不会视为目标障碍物，即使距离可能在探测距离范围，所以上位机视频框没有显示出该车辆。同样从图5（c）路测情况显示结果图可知，如果测试车左后方有车靠近，不会被判断为移动目标，上位机视频窗口同样没有显示该车辆。在道路上的实时测试共测五组数据，且规定每组总的显示车辆数为100，然后记录每组的漏报车辆数和误报车辆数，记录路测试验结果如表6所示。

表6 路测试验结果统计表

从表6的路测统计可知，汽车防撞雷达系统，其漏报率为2.79%，误报率为2.436%，系统误差最大概率为8.1%，最小误差概率为3%，本次测试的平均误差为4.904%。

5 结论

本文主要围绕雷达系统体制进行了研究与分析，主要研究MFSK调制系统测速测距原理。根据模糊函数图，借助MATLAB软件仿真，对比定性分析MFSK调制和LFMCW调制固有分辨率和模糊程度，结果图显示MFSK调制系统分辨能力要优于LFMCW调制。而且对于汽车雷达防撞系统，在道路的复杂环境中，雷达系统应该具有准确识别多个目标的能力。就目前而言，车载雷达多采用LFMCW方式，但是LFMCW存在很大缺点就是在多目标的情况下，会出现虚假目标。通过MATLAB搭建多目标复杂环境，仿真验证MFSK调制能够解决虚假目标问题，本文最终采用MFSK调制方案。最后将该系统安装在汽车上进行实时路测，从上位机视频窗口的测试结果显示，能够正确测得在测试范围内（汽车正后方，盲区）的所有目标车辆，验证了MFSK调制系统设计的可行性，根据路测数据统计，汽车防撞雷达系统其漏报率为2.79%，误报率为2.436%，系统误差最大概率为8.1%，最小误差概率为3%，本次测试的平均误差为4.904%。

参考文献

1. 赵海存.道路交通事故数据统计分析系统研究[D]．长安大学，2005．

2. Lee M S，Kim Y H．Design and Performance of a 24-GHz Switch-Antenna Array FMCW Radar System for Automotive Applications[J]．IEEE Transactions on Vehicular Technology，2010，59(5)：2290-2297．

3. Pourmottaghi A，Taban M R，Norouzi Y，etal．A robust.CFAR detection with ML estimation[C]．Radar Conference，2008．RADAR'08．IEEE．IEEE，2008：1-5．

4. Haikun Jia，Baoyong Chin，Lixue Kuang．A 77 GHz FMCW radar transmitter with power amplifier in 65 nm CMOS [J]．Microelectronics Journal．2014：898-903．

5. 徐小剑，黄培康．雷达系统及其信息处理队[M]．北京：电子工业出版社，2010：69-83．

6. FAULKNER S，BEE P.Experiences，perspectives and priorities of people with schizophrenia spectrum disorders regarding sleep disturbance and its treatment：a qualitativestudy[J].BMC Psychiatry,2017,17(1):158-175．

7. 张发华，舒琳，邢晓芬．头皮脑电采集技术研究[J]．电子技术应用，2017，43(12):3-8．

8. MILES H M，DOLS J D，DILEO H A．Improving provider AASM guideline adherence for adult obstructive sleep apnea[J].Journal.for Nurse Practitioners，2017，13(6)：277-281．

9. MARINO M，LI Y．Measuring sleep：accuracy，sensitivity，and specificity of wrist actigraphy.compared.topolysomnography[J].Sleep,2013,36(11):1747-1755．

10. 谢宏,李亚男,夏斌,等.基于ADS1299的可穿戴式脑电信号采集系统前端设计[J].电子技术应用，2014，40(3):86-89．

11. 宋永坤，蒋留兵，车俐.MFSK雷达系统设计与实现[J]．电子技术应用,2018,44(08):69-72+77.

12. 吴鱼榕.车防撞雷达预警系统中关键技术的研究[D]．电子科技大学，2009．

13. 汤家俊．24GHz调频连续波雷达前端的研究和设计[D].安徽大学,2017．

14. 姜文刚．汽车防撞雷达信号处理及电路设计[D]．电子科技大学，2014．

15. 刘军辉，陈宏滨．基于FMCW雷达测距的车辆防碰撞系统[J]．桂林电子科技大学学报，2016，36(05)：349-354．