武警警官学院 基础部,四川 成都 610213
摘 要:正态总体在教学科研和社会统计活动中都有重要的应用,对正态总体参数的假设检验的深层探讨显得尤为重要。对正态总体参数![]() 的单边假设检验问题,运用理论分析、论证推导、案例解析相结合的方法,解决在检验统计量的分布不确定的情况下,分析如何确定拒绝域的形式,讨论调换原假设和备择假设可能产生相互矛盾的检验结果,并应用结果到具体的例子中,对从事相关理论研究的人员有一定的启发作用。
的单边假设检验问题,运用理论分析、论证推导、案例解析相结合的方法,解决在检验统计量的分布不确定的情况下,分析如何确定拒绝域的形式,讨论调换原假设和备择假设可能产生相互矛盾的检验结果,并应用结果到具体的例子中,对从事相关理论研究的人员有一定的启发作用。
关键词:正态总体;检验统计量;拒绝域.
1 引言
正态分布在生产生活、工程技术、医学、军事等领域都有广泛的应用,假设检验是基于实际推断原理引出的一套理论,在统计学中占有重要地位,对正态总体参数的假设检验在教学中是重点问题,是必须要讲授的知识点。当总体![]() 的分布服从正态分布
的分布服从正态分布![]() ,但其中含有参数
,但其中含有参数![]() 时,需要对未知参数进行参数估计和假设检验,从总体中抽取样本容量为
时,需要对未知参数进行参数估计和假设检验,从总体中抽取样本容量为![]() 的简单随机样本
的简单随机样本![]() [1],通过对样本的统计分析,达到对参数的估计和检验。
[1],通过对样本的统计分析,达到对参数的估计和检验。
姚小娟等人研究了正态总体方差的假设检验与总体均值的联系[2]。本文围绕参数![]() 的情况讨论均值
的情况讨论均值![]() 的假设检验这个主题展开,在具体的教学过程中,存在几个问题:(1)检验统计量的选取,及检验统计量的分布是否确定;(2)拒绝域的形式;(3)原假设和备择假设的确定,及能否随意调换。本文针对这些问题进行探讨,争取达到拨云见日的效果,相关讨论方法可以应用到正态总体方差的单边假设检验中。
的假设检验这个主题展开,在具体的教学过程中,存在几个问题:(1)检验统计量的选取,及检验统计量的分布是否确定;(2)拒绝域的形式;(3)原假设和备择假设的确定,及能否随意调换。本文针对这些问题进行探讨,争取达到拨云见日的效果,相关讨论方法可以应用到正态总体方差的单边假设检验中。
2 问题分析
一、当总体的标准差![]() 已知的情况
已知的情况
当总体![]() ,对于均值
,对于均值![]() 的单边检验问题,分为两种,即右边检验和左边检验,我们以右边检验为例。
的单边检验问题,分为两种,即右边检验和左边检验,我们以右边检验为例。
一般式为:![]() ,
,![]() 为原假设,
为原假设,![]() 为备择假设。
为备择假设。
由于样本均值![]() 是总体均值
是总体均值![]() 的无偏估计,所以当
的无偏估计,所以当![]() 为真的前提下,犯第一类错误(弃真错误)的概率不能超过事先给定的
为真的前提下,犯第一类错误(弃真错误)的概率不能超过事先给定的![]() [3],即
[3],即![]() ,其中
,其中![]() 取值很小,一般取0.05。
取值很小,一般取0.05。![]() 为显著性水平,接下来需要确定
为显著性水平,接下来需要确定![]() 的取值。
的取值。
由于样本![]() 是相互独立的,且与总体
是相互独立的,且与总体![]() 同分布,故
同分布,故![]() ,对
,对![]() 进行标准化得
进行标准化得![]() ,则
,则![]() [4]。根据标准正态分布上分位点的定义 ,得
[4]。根据标准正态分布上分位点的定义 ,得![]() ,其中
,其中![]() 为标准正态分布的上
为标准正态分布的上![]() 分位点。
分位点。
当![]() 为真时,有下列事实成立
为真时,有下列事实成立 ,则
,则
 ,
,
那么 ,
,
通过上述的分析, 的分布虽然不确定,但是可以作为检验统计量。在显著性水平
的分布虽然不确定,但是可以作为检验统计量。在显著性水平![]() 下,该问题的拒绝域为:
下,该问题的拒绝域为: ,即检验统计量
,即检验统计量 的观察值
的观察值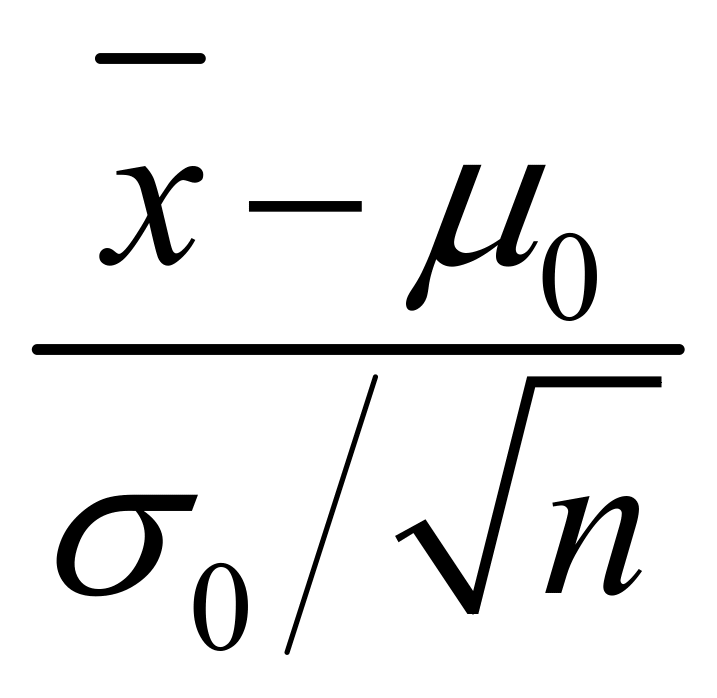 落在
落在![]() 内。若满足则拒绝原假设,接受备择假设。最终决策正确的可能性是
内。若满足则拒绝原假设,接受备择假设。最终决策正确的可能性是![]() ,作出错误决策的可能性为
,作出错误决策的可能性为![]() 。
。
二、当总体的标准差![]() 未知的情况
未知的情况
同以上第一步分析,当总体的标准差![]() 未知时,由于
未知时,由于![]() [5],其中
[5],其中![]() 是自由度为
是自由度为![]() 的
的![]() 分布,
分布, 为样本标准差。
为样本标准差。![]() 分布所对应的连续型随机变量的密度函数曲线在平面直角坐标系中也是单峰且关于纵轴对称,与标准正态随机变量的密度函数类似。同理虽然
分布所对应的连续型随机变量的密度函数曲线在平面直角坐标系中也是单峰且关于纵轴对称,与标准正态随机变量的密度函数类似。同理虽然 的分布不确定,但是可以作为检验统计量。
的分布不确定,但是可以作为检验统计量。
在显著性水平![]() 下,该问题的拒绝域为:
下,该问题的拒绝域为: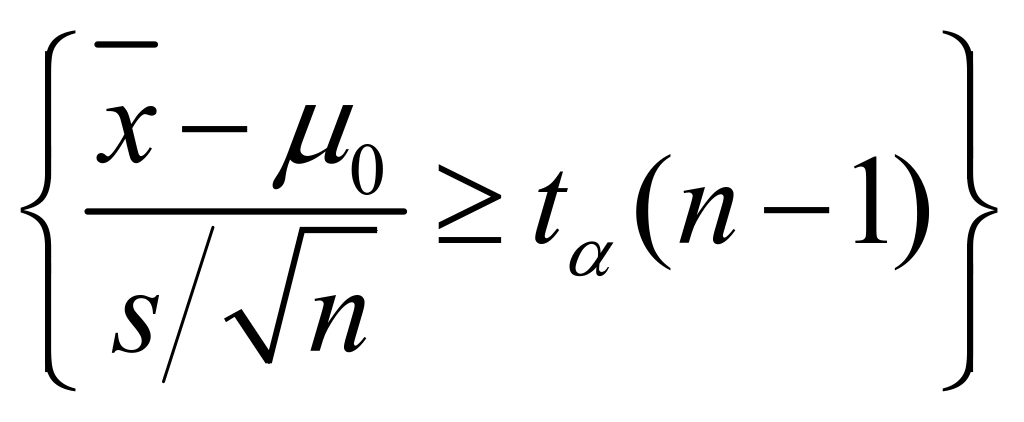 ,其中
,其中![]() 为自由度为
为自由度为![]() 的
的![]() 分布的上
分布的上![]() 分位点,拒绝域也就是检验统计量
分位点,拒绝域也就是检验统计量 的观察值
的观察值![]() 落在
落在![]() 内。若满足则拒绝原假设,接受备择假设。
内。若满足则拒绝原假设,接受备择假设。
三、原假设和备择假设的确定
假设检验的原理是实际推断原理,即在一次试验中,小概率事件几乎不会发生。一个大概率事件发生了,人们认为是正常的,但是一次试验中一个小概率事件发生,人们就认为是不正常的。在显著性水平![]() 下进行假设检验,是通过控制犯第一类错误的概率不超过
下进行假设检验,是通过控制犯第一类错误的概率不超过![]() 而获得拒绝域。即在原假设成立的条件下,拒绝原假设,
而获得拒绝域。即在原假设成立的条件下,拒绝原假设,![]() 。我们有
。我们有![]() 的把握拒绝
的把握拒绝![]() 是正确的决策,反过来接受原假设就显得没有说服力。双侧假设检验针对的是一些参数指标过大和过小都不符合要求的问题,在这类问题中主要证明总体的某个参数是否等于某个特定值。思路是把等号放在原假设中,其基本形式为:
是正确的决策,反过来接受原假设就显得没有说服力。双侧假设检验针对的是一些参数指标过大和过小都不符合要求的问题,在这类问题中主要证明总体的某个参数是否等于某个特定值。思路是把等号放在原假设中,其基本形式为:![]() 。
。
在应用假设检验解决一个具体的单边检验问题中,用同样的方法,同一组样本观察值,有时结论与原假设的形式无关,有时有关。在与原假设的形式有关时,随意调换原假设和备择假设后,最终决策都是接受原假设,而调换前后原假设是对立的,这时候就会出现相互矛盾的检验结果。若在一次检验中,调换前后都是通过接受![]() 获得的,此时都没有很高的可信度,此时选择哪个结论取决于经验和意愿。
获得的,此时都没有很高的可信度,此时选择哪个结论取决于经验和意愿。
根据以上的分析,做原假设和备择假设的问题应该重点放在备择假设上面[6],是在显著性水平![]() 下针对
下针对![]() 检验
检验![]() ,基本原则是:在进行单侧检验时,把我们希望证明的结果放在备择假设
,基本原则是:在进行单侧检验时,把我们希望证明的结果放在备择假设![]() 上,而把不愿接受期待拒绝的假设放在原假设
上,而把不愿接受期待拒绝的假设放在原假设![]() 上,现在进行一次试验,事件
上,现在进行一次试验,事件![]() 就发生了,这与实际推断原理相矛盾,从而就拒绝原假设
就发生了,这与实际推断原理相矛盾,从而就拒绝原假设![]() 。
。
解决问题
例:设某省2020年普通高等学校自主招生考试全体理科考生的总成绩服从正态分布,从中随机抽取某地区1000名考生的成绩,测得平均成绩为447.59分,标准差为90分,问在显著性水平0.05下,是否可以认为本次考试全体考生的平均成绩高于435分?
解:设该省2020年普通高等学校自主招生考试全体理科考生的总成绩为总体![]() ,
,![]() 为未知,在显著性水平
为未知,在显著性水平![]() 下,检验以下问题:
下,检验以下问题:
![]() 分,
分,
该问题的拒绝域为: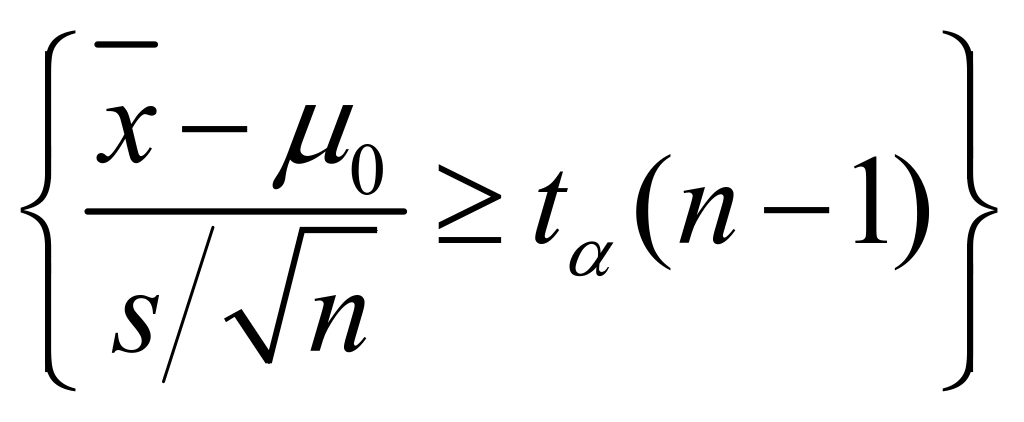 ,其中
,其中![]() ,
,![]() 分,
分,![]() 分,
分,![]() ,代入数据计算得:
,代入数据计算得: ,通过Matlab软件计算
,通过Matlab软件计算![]() ,检验统计量的观察值落入拒绝域,则拒绝原假设,接受备择假设,即认为全体考生的平均成绩高于435分。
,检验统计量的观察值落入拒绝域,则拒绝原假设,接受备择假设,即认为全体考生的平均成绩高于435分。
4 小结
本文对正态总体均值的单边假设检验进行了全面的分析,并把结果运用在具体题目上,注重将应用能力的培养融入到课程教学中,希望本文对广大读者有所帮助和启发。
参考文献
[1] 盛骤,谢式千,潘承毅. 概率论与数理统计(第四版)[M] . 北京:高等教育出版社, 2008.
[2] 姚小娟, 吕陇. 浅谈正态总体方差的假设检验与总体均值的联系[J]. 河北北方学院学报(自然科学版), 2011(05):28-30.
[3] 贾俊平,何晓群,金勇进. 统计学(第7版)[M] . 北京:中国人民大学出版社, 2018.
[4] 陈世高. 对单侧U—检验统计量的讨论[J] . 襄樊学院学报, 2004(02):87-89.
[5] 曲中宪, 武文华. 2个正态总体参数的一类单边检验研究[J] . 吉林林学院学报, 2000, 16(3):168-170.
[6] 黄发贵. 单侧假设检验中备择假设的设定依据[J]. 统计与决策, 2006(7).
王治(1987—),男,山西太原市人,讲师,硕士,从事工程数学教学研究