影响边坡稳定因素分析

影响边坡稳定因素分析

魏明星 1 谷明宇 2

1 西藏自治区水利电力规划勘测设计研究院 西藏 拉萨 850000

2 内蒙古自治区赤峰市林西县应急管理局 内蒙古 赤峰 024000

摘 要： 基于Geo-slope软件，采用摩根斯特-普莱斯（Morgenstern-Price）法求解不同参数条件下的49个均质边坡的安全系数。计算出各影响因素变化与边坡稳定系数变化的大小, 从而确定各因素对均质边坡稳定系数变化的敏感性大小。结果表明, 土体的粘聚力、内摩擦角对边坡稳定性的影响最为敏感, 坡角、坡高的影响次之, 为实际边坡工程的合理有效设计及边坡治理提供了参考。

关键词： 边坡安全系数;参数影响; 摩根斯特-普莱斯（Morgenstern-Price）法

1 引 言

在边坡工程中，影响边坡稳定除了有岩土性质、风化作用、水的作用等地质物理参数，还有地形地貌的几何形状的影响，比如临空面的存在及其坡度的的陡缓都直接与边坡的安全系数直接相关。它们对边坡安全稳定敏感程度有的敏感大, 有的敏感小，但在这些几何、地质物理参数由于量纲不一样，不可能直接比较出这些参数对边坡稳定贡献程度。

边坡稳定系数影响因素的敏感性分析 , 是指定量地分析影响边坡稳定的各因素与边坡稳定系数之间的相关性 ,即分析各因素的变化对于边坡稳定安全系数的变化幅值。在本文中通过在均质边坡众多的影响因素中，依次改变单个因素找出导致边坡失稳的主导因素 。

目前,关于边坡稳定影响因素的敏感性研究 ,许多学者作了大量的工作^{[ 1-5]} ,取得了不少成果。但对各因素敏感性分析结果却存在一定的差异 ,如文献^{[ 2]} 中认为土体内摩擦角为主要影响因素 ,粘聚力及 地下水以及高度次之;文献^{[ 3]}中认为土质边坡破坏形式沿某一圆弧滑移破坏时(包括线形滑动破坏)最重要的影响因素为坡高和坡角 ,在排除边坡线形破坏的特殊情况后 ,最重要的影响参数才是粘聚力和坡角;文献^[4] 中认为参数的敏感性由大到小为粘聚 力、内摩擦角;文献^{[ 5]} 中认为参数敏感性由大到小为粘聚力、重度、内摩擦角 。

本文基于Morgenstern-Price法,对某一土质边坡求解稳定系数, 然后将其中的一个影响因素在基准值附近变化 ,同时保持其他因素水平不变,计算出该因素不同取值条件下的边坡稳定系数。按照同样的方法, 再计算出其他影响因素变化时所对应的稳定系数值。最后利用灰色系 统理论中灰色相关联分析, 得到影响边坡稳定因素的关联序,比较敏感性大小,进而得到影响土质边坡 稳定的主导及次要因素。

2 摩根斯特-普莱斯（Morgenstern-Price）法

在众多的极限平衡法中，摩根斯特-普莱斯法充分满足条块间力和力矩平衡，是严格的极限平衡分析方法，且滑动面形式不限，同时这一方法可以回归到大部分稳定分析的简化计算方法。摩根斯特-普莱斯法首先对任意曲线形状的滑裂面进行分析，导出满足力的平衡及力矩的平衡微分方程。假定相邻条块间的法向力与剪切力之间存在一个对水平方向坐标的函数关系，根据整个滑动土体的边界条件求解，相对Bishop方法只考虑水平力的计算结果相对保守，于一般认为若无数值分析问题，计算结果是精确的。即

X=Ef(x) （1）

式中f(x)--条块间的法向力与剪切力之间存在水平方向的函数关系式，f(x)=c为相当于Spencer方法;f(x)=0为相当于Bishop方法,如图1-1所示。

图1-1 摩根斯特-普莱斯法表示的任意形状的土坡

3 灰色关联分析的基本原理和方法

灰色关联分析是灰色系统理论的一个组成部分，灰色系统理论由我国学者邓聚龙教授在1982年创立,是一种研究少数据、贫信息不确定性问题的新方法^[6] 。这种方法在有限数据条件下可以比较精确的寻找到各种比较因素与参考因素之间的关联程度，关联度越大表明比较因素与参考因素的相关性越强，具体步骤是:首先将影响边坡稳定性的因素定义为比较列 X, X =[ X 1 , X2 , …, X m] ^T ,相应的边坡稳定系数作为参考列Y ,Y =[ Y 1 , Y 2 , … ,Y m ] ^T 。然后对各序列进行数据无量纲化,使得序列具备可比性,最后求得灰关联系数矩阵与灰关联度^{[ 4]} 。

3.1 比较列矩阵与参考列矩阵的定义

首先以影响边坡稳定性的各因素（如粘聚力c 、内摩擦角φ、土体重度γ、坡角θ、坡高 h 等）定义比较列 X:

X= （2）

相应边坡安全系数参考列Y:

Y= 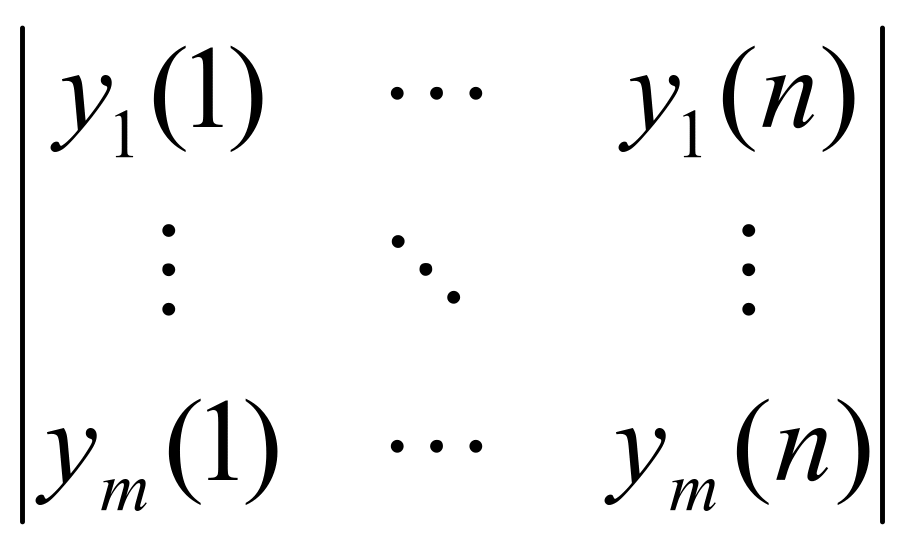（3）

式中:m 为影响边坡稳定因素数目;n为各因素变化值数目。

3.2 矩阵的无量纲化

由于比较列 X 及相应参考列Y 中的各量纲不同且可能相差较大, 无法进行直接比较 ,故需对原始数据作处理转换,使得具有可比性,即需进行矩阵的无量纲化。本文采用初值化法对数据矩阵进行无量纲化处理后上式(2)、式(3)变为：

X i′=[ X i′(1), X i′(2), … , X i′(n)] (4)

Y i′(1)=[ Y i′(1), Y i′(2), …, Y i′(n)] (5)

式中： ; ( i=0，1，……7;j=1,2……7)

3.3 求灰关联系数及灰关联度

灰关联分析的实质是数列曲线间几何形状的相 似程度,曲线越接近 ,相应的数列之间的关联程度就越大 ,因此 ,以曲线间差值的大小作为关联程度的衡量尺度。关联系数的计算公式为:

(6)

为分辨系数, 取值在0与1之间, 越小，关联系数差异越大，区分能力越强，通常情况下取值0.5 。

由于相对于各因素的变化关联系数数目较多,且相对比较分散,为了便于比较,常采用各相关因素的关联度进行比较。关联度的计算公式为。

(7)

影响边坡稳定因素的关联度值在［0，1］之间，值越大说明该影响因素对边坡稳定系数的影响越大,即其敏感性越大;反之,则越不敏感。通过得到各影响因素的关联度,进而得到关联度大小顺序,则可得到相应于各影响因素的关联序列 ,从而得到影响边坡稳定的主要因素。

5 结论

通过计算结果分析,在影响边坡稳定系数的诸多因素中,土体的粘聚力、内摩擦角对边坡稳定性的影响最为敏感,即为影响边坡稳定的主导因素；坡角、坡高的影响为次要因素。

参考文献：

[ 1] 刘立鹏, 于红杰.力学、几何参数对土质边坡稳定的敏感性分析[ J] .岩土工程技术, 2008 , 26(3) .

[ 2] 陈志波, 简文彬.边坡稳定性影响因素敏感性灰色关联分析[ J] .防灾减灾工程学报, 2006 , 26(4):473- 477.

[ 3] 肖桃李, 李新平, 米 健.土质边坡稳定性影响因素的 研究[ J] .地质灾害与环境保护, 2007 , 18(2):89-93 .

[4] 张鲁渝, 郑颖人, 赵尚毅, 等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[ J] .水利学报, 2003(1):21-27 .

作者简介：第一作者魏明星（1987-），男，重庆巫山县 硕士生，工程师，主要从事水工结构设计及其岩土工程计算工作。