四川省广安第二中学校 四川 广安 638000
摘要:所谓面积法,就是运用面积关系解决平面几何的方法.在初中几何题中的线段长度、线段相等(不等)、角相等、比例式或等积式等,虽然几乎都可以用其他方式来解决,但是有时面积法无疑是一种简单,直接,有效的方法.
关键词:面积法;平行四边形;几何;解题;
面积法实际上是数形结合的范畴,渗透于初中数学教学和解题中.面积法可以把已知和未知量用面积公式联系起来,从而将几何元素之间的关系变成数量关系,以形补数,以数推形,数形结合的方式让问题化繁为简.
利 用面积法求线段的长
用面积法求线段的长
例
图1
1.如图1,AC和BD是 ABCD的对角线,相交于点O,AE和BC垂直,垂足为E,AB=
ABCD的对角线,相交于点O,AE和BC垂直,垂足为E,AB= ,AC=2,BD=4,求AE的长.
,AC=2,BD=4,求AE的长. 分析:通过平行四边形的性质可推出AO,BO的长度,根据勾股定理逆定理可以得到三角形ABO是直角三角形,联系平行四边形的面积公式即可
得到AE的长.
解析:∵四边形ABCD是 ,
,
∴AO=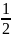 AC=
AC= 1,BO=
1,BO=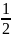 BD=
BD= 2. ∵AB=
2. ∵AB=
∴ , ∴∠BAC=
, ∴∠BAC= .
.
∴在 BAC中,
BAC中, =
=
 ,
,
∴ , ∴AE=
, ∴AE= .
.
评析:上述面积法用到了等量转化思想,利用同一个图形面积算两次,构成一个方程,将几何代数化,抽象具体化.
二、利用面积法求线段的最值问题
例
 2.如图2,在
2.如图2,在 ABC中,∠BAC=
ABC中,∠BAC= ,且BA=3,AC=4,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M, DN⊥AC于点N,连接MN,求线段MN的最小值.
,且BA=3,AC=4,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M, DN⊥AC于点N,连接MN,求线段MN的最小值.
图2
图2-1
分析:三个角都是直角可证得四边形ABCD是矩形,由矩形对角线相等得出MN=AD,把问题转化为求AD的最值,根据点到线之间垂线段最短和面积法即可得到AD的最小值,即MN的值.
解析:连接AD,MN(如图2-1),
∵DM⊥AB,DN⊥AC,∠BAC= ,
,
∴四边形DMAN是矩形,∴MN=AD,
当AD⊥BC时,AD的值最小.
在 ABC中,根据勾股定理可得:
ABC中,根据勾股定理可得: ,
,
∴ =
=
由 可得AD=
可得AD= ,
,
即MN的最小值为 .
.
评析:上述将MN转化为AD,是解题的关键之处,经过这样的转化后,利用AD与BC的垂直关系即可和面积公式联系起来.
三、利用面积法求线段的和
例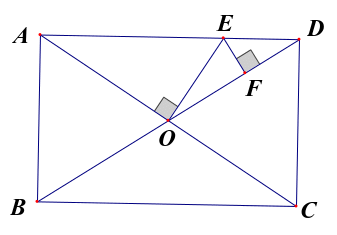 3.如图3,在矩形ABCD中,AB=6,BC=8,过点O作OE⊥AC,交AD于点E。过点E作EF⊥BD,垂足为F,则OE+EF的值.
3.如图3,在矩形ABCD中,AB=6,BC=8,过点O作OE⊥AC,交AD于点E。过点E作EF⊥BD,垂足为F,则OE+EF的值.
分
图3
析:△AOD可以看作被OE,EF分为的△AOE和△EOD,由OE垂直AO,EF垂直OD,把△AOD的面积分割成△AOE和△EOD的面积和,即可转化成线段OE,EF的和.解析:∵四边形ABCD是矩形
在 ABC中,根据勾股定理:
ABC中,根据勾股定理:

∴AO=DO=5
∴
∵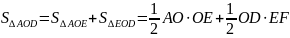


∴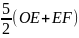 =12 ∴
=12 ∴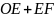 =
=
评析:本题面积法的巧用,相比设未知数根据勾股定理等求解的方法更为简单易算,可谓出奇制胜.
四、利用面积法求菱形中最值问题
例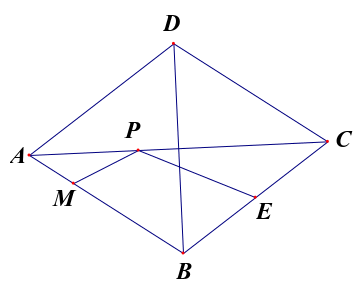
 4.如图4,在菱形ABCD中,AC=
4.如图4,在菱形ABCD中,AC= ,BD=6,E是BC边的中点,P、M分别是AC、AB上的动点,连接PE、PM,则PE+PM的最小值.
,BD=6,E是BC边的中点,P、M分别是AC、AB上的动点,连接PE、PM,则PE+PM的最小值.
图4-1
图4
分析:在点P,E和M这三点中,E为定点,故首先考虑点E,根据点E位置的特殊性,可作点E关于AC的对称点 ,由对称性可得,P
,由对称性可得,P 所以PE+PM=P
所以PE+PM=P +PM,问题转化为:两线
+PM,问题转化为:两线 三点
三点 两点
两点 一线一点,根据垂线段最短,即将问题转换为求
一线一点,根据垂线段最短,即将问题转换为求 M,结合菱形的两种面积公式即可解决.
M,结合菱形的两种面积公式即可解决.
解析:如图4-1,根据对称性得:PE+PM=P +PM=
+PM= .当P、M、
.当P、M、 三点共线且
三点共线且 M⊥AB时,PE+PM取得最小值.易得AB=3
M⊥AB时,PE+PM取得最小值.易得AB=3 ,又
,又 即
即 ,解得
,解得 ,即PE+PM的最小值是
,即PE+PM的最小值是 .
.
评析:上述整个解题思路多次用到了转化思想,平行四边形和最短路劲相结合,这也是本题中不易想到的一步,结合条件和辅助线利用面积法,使得问题迎刃而解.
面积法求两线段最值问题不仅局限在平行四边形、矩形或菱形中,也可以迁移到等腰三角形或者三角形中.
变式训练:△ABC中,AB=AC=5,BC=8,点P在BC边上,过点P作PD垂直AB,垂足为D,PE垂直AC,垂足为E,则PD+PE的长是.
面积法求两线段最值问题不仅局限在菱形中,也可以迁移到等腰三角形中
其实不难看出,以上几类题中给出的条件和解法都有“垂直”这一共同特点,而无论是三角形面积中的“底”和“高”,平行四边形面积中的“底”和“高”,还是矩形面积中的“长”和“宽”,菱形面积中的两对角线,它们之间的关系也都是“垂直”的关系.这种“垂直”自然而然地成为了面积法和几何题之间的纽带。由此可以归纳得到,在解决一些关于垂直的线段问题中,除了常用的方法之外,还可以考虑到用面积法求解.
面积法的运用是广泛的,不仅仅是在初中数学几何解题中,乘法公式、整式的乘法和勾股定理等教学中也都有面积法的参与,甚至在“重建三角”视域下,
 也是用面积法来定义的以及一系列对面积法的巧用.
也是用面积法来定义的以及一系列对面积法的巧用.
参考文献:
[1]刘晓东.面积法在几何解题中的应用[J].初中数学教与学,2013,{4}(15):28-30.
[2]覃秀芬.巧用面积法突破几何题[J].中学教学参考,2020(11):14-15.
[3]侯京周.面积法在解题中的运用[J].初中数学教与学,2020(07):24-25+39.
[4]马先龙.例谈如何利用面积法解几何题[J].数理化学习(初中版),2020(01):16-18.