高德地图API及Floyd算法在通勤路径优化中的探索

高德地图 API及 Floyd算法在通勤路径优化中的探索

孙杨 徐剑桥 刘净含 潘维运

沈阳工业大学理学院数学系 辽宁 沈阳 100870

摘要：通勤路径优化问题研究中，大多数文献采用目标乘车点之间的线性距离之和最短作为最优解的求解结果。但在实际道路中，乘车点之间存在诸多因素，使得通过线性距离之和最短作为最优路径结果和实际场景存在一定偏差。因此本文提出了结合高德地图API和Floyd算法将理论运用于实际情形，利用高德地图获取的目标乘车点之间的适时实际驾车距离并通过Floyd算法将进行最优路径求解。通过实验结果分析表明，本文的方法具有一定的可行性和实用性。

关键词：Floyd算法；高德地图API；满意度；最优解；

1 引言

随着社会经济的发展，许多单位面临着通勤的问题，，企业有效地安排车辆并让职工尽量满意是个十分重要的问题。而通勤路径优化问题研究中，大多数文献采用目标乘车点之间的线性距离之和最短作为最优解的求解结果。但是在实际的道路目标乘车点之间会存在诸多因素导致与目标乘车点之间的线性距离相差甚远。由此我们以研究沈阳市铁西区经济开发区某单位的通勤问题为例，提出了一种首先通过高德地图API^[1]获目标乘车点之间的适时实际驾车距离，再由Floyd算法进行优化得到最优解，从而有效地将理论与实际通勤路径相结合，具有一定的可行性和实用性。

2 通勤路径优化的数学模型及其求解

我们以沈阳市铁西区经济开发区某单位为研究对象，我们利用高德地图API得到职工住址的经度和纬度并利用高德地图API做出职工住址分布图（见图1），本文采用Floyd算法将住址分布图划分为40个区，得到各区的距离表与各区人员分布表。

2.1 Floyd算法简介

Floyd算法是弗洛伊德提出的一种解决每对节点之间最短路径问题的的算法。

算法的基本思想：直接在图的带权邻接矩阵中，用插入顶点的方法依次构造出v个矩阵D⁽¹⁾、D⁽²⁾、…、D^(v),使最后得到的矩阵D^(v)为图的距离矩阵，同时也求出插入点矩阵以便得到两点间的最短路径。通过Floyd算法得到最短路距离矩阵B^*(i,j)。

2.2 模型的建立

在上述最短路距离矩阵B^*(i,j)的基础上，分析建立n个乘车点的情况：由于每个区的职工都选距离本区最近的乘车点乘车，引入变量 ，表示第个k区域到最近乘车点的距离,然后，求出40个区域到各自最近乘车点的驾车最短距离之和

2.3 建立满意度函数

如果车站就建在自己的区，则职工就非常的满意，如果离自己区最近的车站比较远，则职工就不满意。职工对车站点的满意度取决于自己区到最近乘车点的距离。为此我们建立满意度函数_k的值越大，满意度就越大。由于每个区职工的满意度不同，每个区的人数也不同，我们不可能使每个区职工的满意度都最大，因此关注的是全体职工的平均满意度^[2],

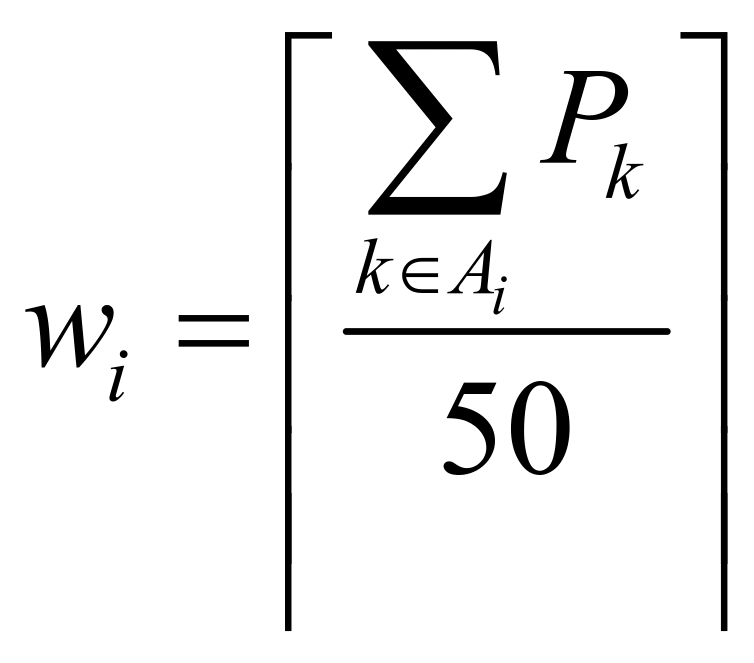所需车辆数w_k的分析。设到第 个乘车点的区域的子集合为_,，由于每个站点的人数不恰好是车辆满载（核载50人）职工数的整数倍，每个站点就有可能有一辆车不能满载，所以当站点数越多，不能满载的车辆数就越多，从而导致所需车辆总数的增加。

2.4最优乘车点和车辆数

通过Matlab仿真运行得到如下结果（仅以n 取2，3，4为例），设立2个乘车点，最优解为区域7和29，平均满意度为0.095，所需车辆数为5；设立3个乘车点时，最优解为区域7、18和35。平均满意度为0.755，所需车辆数为6；设立4个乘车点时，最优解为区域7、17、26和36，平均满意度为0.786，所需车辆数为7.由此可见满意度增加的同时，车辆数也在增加，故企业应该根据通勤成本的预算情况下，合理地按排乘车点及车辆数。我们建议乘车点数目设置为

3至6个．这样既能满足职工的满意度大，又能最有效的进行车辆安排，节省运行成本。

图1：职工住址分布图

参 考文献

[1]刘庆华,汪晶.高德地图及改进 ACA 在车辆路径寻优中的应用[J].计算机与数字工程.2020.48(6) 1354-1359.

[2]杨豪,刘云.校车的最优化安排问题.城市建设理论与研究.2012(20)