叶城县第三中学 新疆 叶城
摘要:圆锥曲线问题是高考的必考内容,且难度很大,属于高考中的难题,用传统方法非常繁琐,本文采用伸缩变换,解决圆锥曲线问题借助单位圆达到化繁为简,化难为易的目的,在此基础上推导了一系列椭圆和双曲线的性质,具有很大的推广价值和意义。
关键词:圆锥曲线;伸缩变换;圆;放射变换
其实很多人的脑海中曾经出现过这样的疑问:椭圆到底是不是圆?它们到底有什么关系?面对圆锥曲线很多神奇有趣的结论和性质,我们非常好奇这些结论的来历。我们知道高考中的圆锥曲线题目的难度比较大,很多人不寒而栗,知难而退,直接放弃这类题,难道这类题真的这么难吗?高考中往往考察比较多的是椭圆问题,而双曲线和椭圆出现的少之甚少,难道这是巧合吗?
我们虽然在选修4-4里学过伸缩变换,但是学的比较肤浅,很多人学的只是在表面上了解,没有深入研究学习过,只停留在三角函数的伸缩变换上,其他方面基本不怎么用。其实我们容易想到通过伸缩变换可以把椭圆化成单位圆,甚至把双曲线和椭圆也可以利用伸缩变换和放射变换来转化成圆来处理,是一个非常不错的方法。
我们知道伸缩变换就是放射变换,而放射变换是一种二维坐标到二维坐标的线性变换,因此伸缩变换也保持二维图形间的相对位置关系不发生变化: 将平行线变为平行线,直线变为直线,并且保持同一条直线上的点的位置顺序和长度的比例关系不变, 对应直线的斜率比保持不变,以及对应图形的面积比保持不变等等。所以我们只要引入一个伸缩变换就可以达到把圆锥曲线转化成圆的目的。
伸缩变换:
对于曲线方程 ,作如下变换
,作如下变换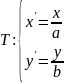 ,则曲线的C的方程变为
,则曲线的C的方程变为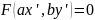 ,点A
,点A 经上述变换为变
经上述变换为变 ,,由上述的变换T的作用下椭圆可以变成单位圆,同样引入伸缩变换
,,由上述的变换T的作用下椭圆可以变成单位圆,同样引入伸缩变换 ,或
,或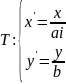 也可以把双曲线转换成单位圆。为了方便约定,变换前后的像用
也可以把双曲线转换成单位圆。为了方便约定,变换前后的像用 区分开,比如线段
区分开,比如线段 变换后的像为|
变换后的像为| ,几何图形面积
,几何图形面积 变换后的像为
变换后的像为 等。
等。
伸缩变换的性质:
在放射变换的基础上我们很容得出下面伸缩变换的性质。
1.点、直线、曲线变换后仍然是点、直线、曲线。
2.直线和曲线的位置关系保持不变。
3.平行直线变换后仍平行、相交直线变换后仍相交。
4.若直线l的斜率为k,缩变换后变换后直线 的斜率为
的斜率为 ,则
,则 ,若斜率
,若斜率 不存在则
不存在则 也不存在。
也不存在。
证明:直线 上任取两点A,B则
上任取两点A,B则 =
=

5.线段 和变换后的线段
和变换后的线段 之间的关系是
之间的关系是
证明:

6.伸缩变换后平行线段比例不变,即若 则
则
证明: 

且
7.几何图形的面积为 ,变换后的面积为
,变换后的面积为 ,则
,则
证明:
所以
8.若曲线 ,则
,则
三、伸缩变换的应用:
1.位置关系判断。
例题1.判断直线 和椭圆
和椭圆 的位置关系。
的位置关系。
解:引入变换 ,其中
,其中 ,则
,则
直线 :
: 在
在 的作用下变为
的作用下变为
 的圆心到直线
的圆心到直线 的距离为
的距离为
所以圆 和直线
和直线 相交,所以椭圆
相交,所以椭圆 和直线
和直线 也相交。
也相交。
2.弦长问题。
例2.若直线 和椭圆
和椭圆 相交于A,B两点,求
相交于A,B两点,求
解: 引入变换 ,其中
,其中 ,则
,则
直线
圆 的圆心到直线
的圆心到直线 的距离为
的距离为 ,
,
则 ,直线
,直线 的斜率
的斜率 ,直线
,直线 的斜率
的斜率
因为
3.面积问题
例3.已知点 ,直线
,直线 和椭圆
和椭圆 相交于B,C两点,求
相交于B,C两点,求 的面积。
的面积。
解: 引入变换 ,其中
,其中 ,则
,则
直线 ,点
,点
圆 的圆心到直线
的圆心到直线 的距离为
的距离为 ,
,
则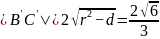 ,点
,点 到直线
到直线 的距离
的距离
 的面积
的面积
所以 的面积
的面积
4.由伸缩变换得到的椭圆的一些重要性质
我们知道在圆中有很多性质,我们可以通过伸缩变换得到椭圆中跟圆类似的性质。
(1)若 是椭圆的长轴或者短轴端点,点
是椭圆的长轴或者短轴端点,点 椭圆上异于
椭圆上异于 的任何一点
的任何一点
则
若 是双曲线的实轴端点或虚轴端点,点
是双曲线的实轴端点或虚轴端点,点 为双曲线上异于
为双曲线上异于 的任何一点,
的任何一点,
则
证明:圆中因为 为直径,所以
为直径,所以
所以
双曲线中
所以
(2)若 是椭圆上的任两点,
是椭圆上的任两点, ,O为原点,
,O为原点,
则 ,
,
若 是双曲线上的任两点,
是双曲线上的任两点, ,O为原点,则
,O为原点,则 ,
,
证明:椭圆中
所以
而
双曲线中的证明同上。
(4)椭圆在点 处的切线方程为
处的切线方程为 ,双曲线在在点
,双曲线在在点 处的切线方程为
处的切线方程为
证明:椭圆中引入变换 ,则点P的变成点
,则点P的变成点 ,椭圆变成单位圆
,椭圆变成单位圆 ,此圆在点
,此圆在点 的切线方程为
的切线方程为 ,还原到椭圆中
,还原到椭圆中
得 ,双曲线中的证明同上。
,双曲线中的证明同上。
(3)椭圆的面积为
证明:因为单位圆的面积 ,因此椭圆的面积
,因此椭圆的面积
例4.已知椭圆 上一点
上一点 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于 轴,直线
轴,直线 与椭圆C交于A、B两点(A、B两点均不在坐标轴上)
与椭圆C交于A、B两点(A、B两点均不在坐标轴上)
(1)求椭圆C的方程
(2)设 为原点,若
为原点,若 的面积为
的面积为 ,试判断直线OA与OB的斜率之积是否定值?若是,求该定值,不是说明理由。
,试判断直线OA与OB的斜率之积是否定值?若是,求该定值,不是说明理由。
解:(1) (过程略)
(过程略)
(2) 引入变换 ,其中
,其中 ,则
,则
由 得
得
因此在单位圆 中
中 为直角三角形,所以
为直角三角形,所以
所以
所以
所以直线 、
、 的斜率之积为常数
的斜率之积为常数

由上述的性质和有关例题以及证明中可以发现伸缩变换展现了圆锥曲线和圆之间的内在联系,我们可以通过伸缩变换圆锥曲线和单位圆巧妙的关联在一起,再用圆来研究圆锥曲线。伸缩变换让我们拥有了一个利器,我们可以通过这个利器把圆锥曲线转化为圆,借助放射变换和圆的有关性质和结论容易得到圆锥曲线中的很多性质和结论,我们也可以容易解决圆锥曲线当中的繁琐题,达到事半功倍的目的。伸缩变换是数学中的一个好的工具,深入学会伸缩变换意义非常大,有很大的研究和推广价值。
参考文献:[1]林国红 抛物线切点弦方程的应用[J].中学数学研究(华南师范大学版)
[2] 钟玉泉 复变函数论.高等教育出版社,2013
[3]同济大学数学系 微积分 高等教育出版社 第三版上册