基于 Matlab/Simulink的过流保护仿真

周心怡

国核电力规划设计研究院 有限公司 北京 100095

摘要：随着科学技术的发展，电力系统的复杂性逐步提高，针对电力系统、继电保护等相关系统、技术的仿真模拟变得越来越重要。本文利用MATLAB的动态仿真软件SIMULINK搭建了电力系统过流保护的仿真模型,得到了故障电流下的仿真结果。在运行本仿真实例的基础上,对仿真结果进行了分析，表明了过流继电保护仿真的有效性和可行性。

关键词:过流保护；继电保护；仿真模拟；Matlab/Simulink

引言：Matlab是于1980年由Cleve Moler创作，并于1984年由Math Works公司出版发行的数学基计算软件。根据MathWorks自己的数据，目前世界上180多个国家的超过三百万工程师和科学家在使用Matlab和Simulink，已成为国际公认的标准计算软件。于2001年推出的Simulink，是Matlab中的一种可视化仿真工具， 是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包。它为用户提供了许多标准控制系统的仿真模块，用户可直接调用模块库中的模块，也可以封装自己的模块，从而建立需要的系统，这一特点为建模带来了极大的便利和效率。

过流保护是电力系统继电保护中最早得到应用的一种继电保护类型。在当下的电力系统种，过流保护常常作为其他保护的后备保护。过流继电器是过流保护的核心元件，针对过流继电器动作特性和动作行为的正确设计和分析，是保证过流保护装置可靠工作的一个核心环节。本文基于Matlab/Simulink对过流保护继电器进行了仿真计算，并在故障情况下对继电器模型的动作特性进行了分析比较，验证了模型的有效性，并加深了对过流继电器性能的理解。

1 过流继电器的仿真模型

本文采用当下广泛使用、具有较高准确性的数字算法针对标准反时限特性的过流继电器进行仿真。数字算法主要包含了对输入信号振幅的测算；累积增量否达到阈值的判断。

故障电流幅值的准确性决定了继电器的精确度。故障电流信号振幅的测算有很多中方法，包括两点式算法、离散傅里叶变换以及快速傅里叶变换等。本文采用离散傅里叶变换处理数据，它有着不受采样频率、信号噪点以及直流分量影响的特点，能够更加准确的测算电流幅值。离散傅里叶变换的数学模型为：

（1）

（2）

（3）

式中，N为采样数量，I_Re和I_Im为电流幅值的实部和虚部，I^为输入电流信号的波峰幅值。

标准反时限特性的动作时间为：

_（4）

则采样数量N可以用动作时间t_op和采样频率f_s表示为：

_（5）

假设经历N个采样点后达阈值C_T，则每一个采样间隔的增量inc都可以表示为：

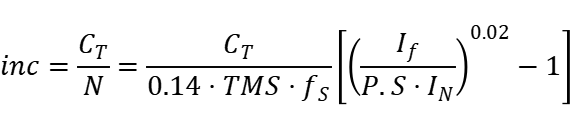_（6）

根据如上公式，使用Simulink框图模式搭建了图下模型。其中离散傅里叶变换直接使用Simulink模型库中的元件来获取信号幅值；计数器当且仅当增量为正值时进行累加计算；当积累结果达到阈值时发出跳闸信号“1”。

_{图1 Matlab/Simulink模型图}

2仿真实验与结果分析

2.1 故障状态下的仿真

本实验的故障电流信号假设为一个sine曲线，在0.1s时信号幅值由354.6A瞬间增至5319A，采样频率设置为1kHz，电流互感器变比设置为300：5，P.S设置为100%，T.S设置为0.09，阈值C_T设置为1000A。仿真结果如图2所示。实验结果显示的跳闸时间为0.25s，与计算结果0.243s存在2.8%的误差，误差在接受范围内，表明本模型准确性较高。经过分析，该误差应该是由于傅里叶变换模块计算的时间延迟引起的。

图2 故障状态下的仿真结果 图3 暂态故障下的仿真结果

2.2 暂态故障下的仿真

除了上一个实验，暂态故障下的性能也是反应继电器性能的重要指标。暂态故障的故障时间比跳闸时间短。在本实验中，电流信号设置为 354.6A 50Hz，P.S设置为100%，T.S设置为0.09，阈值C_T设置为1000A，故障设置在0.1s到0.2s之间。仿真结果如图3所示。结果显示，本实验模型未跳闸，计数器在0.219s归零，经过与理论值的对比，存在8.6%的误差，误差在接受范围内，表明本模型准确性较高。经过分析，该误差应该是由于傅里叶变换模块针对暂态故障的计算存在两个周期的时间延迟。

结语：根据过流保护动作原理及数学原理，基于Matlab/Simulink搭建的过流保护动态仿真模型，达到了模拟过流保护动作过程的基本目的。对模型的搭建过程以及不同故障状态下的仿真结果进行了具体的分析，虽然离散傅里叶模块的计算特性给本模型带来了微小的误差，但总体来看该模型有着较高的准确性，为进一步利用Matlab/Simulink研究继电保护系统提供了思路和方法。

参考文献：

[1]许明，高厚磊，侯梅毅等。数字仿真技术在继电保护教学中的应用。电力系统保护与控制，2010，38（15）：104-109

[2]J. Duncan Glover, Mulukutla S. Sarma and Thomas J. Overbye, “Power System Analysis nd Design”, Fifth Edition. 2012.

作者简介：周心怡，女，（1990.10-），籍贯：山东 曲阜 学历：硕士研究生 职称：工程师