关于脱模力的研究及在此基础上对脱模凸轮的优化

关于脱模力的研究及在此基础上对脱模凸轮的优化

李永昌

南京东田精密机械有限公司南京211100

摘要：脱模力是设计粉末成型设备的主要指标，也是粉末成型压制品选择成型压机的重要参考；但是脱模力的计算由于涉及的到因素很多，一直以来都是通过经验估算，也就是按照压制成型力一半来预估，这样往往与实际值差别较大；本文从多孔材料的泊松比的角度计算成型制品的脱模力，通过动、静摩擦系数不同，结合脱模力正压面积的变化得出脱模力的变化过程，画出变化趋势图，进而对现有的粉末成型压机脱模凸轮进行优化。

关键词：脱模力、泊松比、干粉成型压机、脱模凸轮

一、背景及现状

在粉末冶金、磁性材料等需要将粉末干压成型的生产过程中都会使用到干粉压机，该设备将松装粉末压制成所需要的形状及强度(密度)的压坯，并从模腔中脱出，这个过程是粉末压制成型零件生产工艺中最重要的工序，能够顺利实现以上的两个过程是检验干粉压机最最要的指标。目前粉末压制成型力有简单公式计算，脱模力目前只能预估为压制力的一半，脱模力的变化趋势也只能预估为由大变小，这样的靠经验来指导生产常常会出现偏差，如果以这样的经验来设计机器，特别是脱模凸轮的设计就不能设计出最适合脱模过程的凸轮曲线。如果可以找到一个准确计算脱模力的方法、找到脱模力变化准确的趋势将对实际生产到来很大的帮助。

二、脱模力的推导思路

脱模力计算是不是可以通过从其产生反向推导哪?按照这个思路我们不妨反推一下，脱模力的产生是粉末压制成型后压坯与凹模腔接触面有剩余的侧向压力，使得凹模腔侧壁对压坯产生的摩擦阻力，该阻力即为脱模力；而剩余侧压力为压坯侧压力在失去粉料压制方向的正压力且压坯回弹膨胀后对凹模侧壁剩余的侧向压力；所谓侧压力则为粉末在受到压制方向的正压力时横向作用于模腔侧壁的力；压坯成型后模壁给压坯一个等量、反向作用力，这种由垂直压力作引起的摸壁给压坯的应力，称之侧压压强，因为正压强与压坯的密度已经有明确的对应关系式，故只要能够找到正压强与侧压强的关系就可以推导出脱模力。

三、侧压强、侧压力

致密材料的横向应变(力)与纵向应变(力)的比值为固定之，我们称之泊松比；液体的每个方向的压强相等，粉末以及被压缩过的压坯，因为其不是致密材料，可以借鉴多孔材料的来进行推算，横向应变(力)与纵向应变(力)的比值ξ是介于两者之间其公式如下：

其中为μ材料的泊松比

该数值是介于1与致密材料的泊松比μ之间的值。

根据胡克定律：可以得到侧压强Ps的与正压强的P计算公式为：

公式中ξ—多孔材料侧压系数；ξ0—致密材料的侧压系数；θ-压坯相对密度；

四、剩余侧压力

压坯成型后，上模回升泄压，先前高应力下变形的压坯和凹模有回弹的趋势，此时凹模壁对压坯产生的压应力为剩余侧压强Psi， 这个压强与侧压强Ps， 模具的刚度m， 模具材料的弹性模量Ea，其计算公式为：

Psi=jPs=j 公式中j为剩余侧压强与侧压强比值

试验证明，当凹模的为合金钢(该材料为最常用的凹模制作材料，是具有代表性的材料) ， 其弹性模量为Ea=2x 10°MPa，泊松比μa=0.3， 其j值与模具的刚度m的比值关系为下表：

注：m—凹模外径与内经的比值，m=D/d

由该实验数据可以得出：随着凹模的刚度的提高(即m值增大) ， 剩余侧压强Psi下降，因而脱模力亦下降。

因铁基生产中产量最大，使用范围最广，该数据已经在铁基粉末冶金生产过程中得到证实，同时试验证明其他材料的j值如铜基、磁性材料、硬质合金均会小于铁基为其80%-95%，为确保计算能正确指导生产，并留有保险系数模具设计、成型设备的选择都参照以上的表格进行。

五、脱模力

压制成型产品的脱模力Fe直接决定于三个因素， 剩余侧压强Psi、压坯与模壁的静摩擦系数f、压坯与模壁的接触面积S，计算公式为：

Fe=f。·Psi·S

其中：f。—压坯与模壁的静摩擦系数，该数值试验的在0.15-0.22

粉末压制成型的过程中摩擦力分为静摩擦力和动摩擦力，脱模的过程中首先要克服模壁对压坯的静摩擦力再克服动摩擦力方能将压坯脱出凹模；试验得知各种常规材料动摩擦系数约为静摩擦系数的60%-70%，故在设计机器及选择成型设备脱模力是指要以克服静摩擦力为标准。

六、脱模力的变化过程

最大脱模力按照以上的推理过程可以计算出，脱模力的变化过程可以根据脱模运动的过程来分析。如下图，压力机开始脱模时首先克服模壁对压坯的静摩擦力，此时脱模力最大这里用位1来表示；一旦凹模持续运动起来，直到凹模上表面与压坯上表面平齐的过程中因为剩侧压强Psi、压坯与模壁的动摩擦系数f以及压坯与模壁的接触面积S都保持不变， 固该脱模力维持不变，约为0.7；凹模继续向下拉时压坯逐渐脱出凹模，这个过程中脱模持续减小直到为0.

脱模开始，脱模力最大克服动摩擦力，脱模力恒定克服动摩擦力，脱模力持续减小

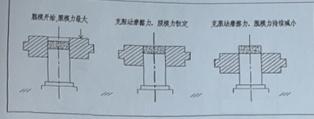
根据以上脱模过程的分析以脱模力为纵坐标压力机主轴角度为横坐标绘制出脱模力变化过程的曲线：(压力机脱模时间为一个成型周期的1/4，对应的主角度为180°-270°为90°)

该曲线可以明确的表示出脱模力随着压力机主轴的运动的变化趋势，在此基础上对脱模凸轮优化就很容易做出适合压力机脱模过程的曲线。

七、脱模凸轮曲线的优化设计

在粉末成型压力机的主电机功率一定的前提下，我们可以通过改变原来匀速脱模的凸轮曲线，改为分段设计，根据功率P计算公式：

P=F.V

公式中F——为脱模力V——为脱模速度

可见功率一定时降低脱模速度能够有效提高脱模力，将脱模力需求最大的开始部分的凸轮曲线设计的更缓和，使得脱模速度较慢；将脱模力需求较小的结束部分的凸轮曲线设计的更尖锐，使得脱模速度较慢；经过这样的简单改动即可提升有效脱模力，设计出适合脱模过程的最佳凸轮曲线。

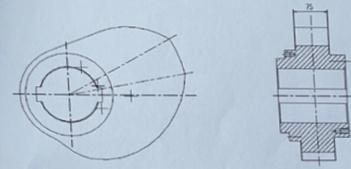
以600kN粉末分型压力机为例简单介绍优化过程，原凸轮见图如下，该凸轮为等速脱模运动：

该压力机的正压强按P=400MPa计算制品比壁厚5cm,最大成型制品直径不超过75cm,制品高70cm,触面积S=16450mm2,m=1.5则j=0.69, f。=0.22查得铁基ξ。=0.38，压

坯相对密度θ=0.9

Pe=f。Psi=f。jξ。θPS

=0.22x0.69×0.38x0.9x400×16450

=341604N≈34吨

该计算结果大于预压制力一半30吨,凸轮的宽度为75cm较为合适,在以上对凸轮曲

线分析该为如下曲线:

八、结论

由以上的分析可以得出按照泊松比推导出剩余侧强,再按照剩余侧压力推导出脱模

力相对准确地计算方法,再按照脱模的实际过程分析的出脱模力的变化曲线,我们能够清晰

反应出整个过程,在实际生产过程中可以准确的指压制制品机器选择机器;在准确计算脱

模力的基础上结合脱模速度与脱模力大小的反比关系设计出的脱模凸轮更能适合实际的脱

模过程。

参考文献

1．张华诚 粉末冶金使用工艺学 粉末冶金工业2004.3

2．韩凤麟 粉末冶金零件实用手册 兵器工业1995.9

3．叶伟昌 机械工程及自动化简明设计手册 机械工业2001

4．苏翼林 材料力学 天津大学2006.01