哈尔滨市国土资源勘测规划院 黑龙江 哈尔滨 150000
摘要:这些年来,随着GNSS技术的不断发展,为以视觉传感器和卫星定位信号为基础的测量技术的发展提供了技术支持。这些年人们对导航和测绘的要求不断提高,一种传感器所提供的定位和感知已经无法满足人们日常的实际需求。因此有必要将视觉传感器与GNSS进行结合,为人们提供更好的测量技术和导航功能。因此本文对GNSS在视觉导航与测量中的应用进行探讨,希望能为我国导航与测量技术的发展提供一些参考。
关键词:GNSS;视觉导航;测量技术
0引言
这些年来,GNSS技术在各个领域中得到了普遍应用,已经逐渐成为了一种成熟的定位技术。在我国GNSS技术也被用于城市交通、抢险救灾、地质灾害监测、渔业以及测绘等领域,为我国经济的发展做出了巨大贡献。在摄影测量领域,许多硬件设备的技术水平不断提高,这也为GNSS在航空摄影测量中的应用提供了物质基础。控制点的精度是测量工作的关键点,也是以往测绘工作中需要花费大量的人力和财力来进行的工作,而现如今,将GNSS技术应用到航空摄影测量之中,可以有效的提高测量精度,满足测量的实际需求,降低测量的成本支出。在导航领域,随着经济的发展人们对导航定位的需求不断增加,并逐渐向着智能化的方向发展。如在工厂中人们需要对货物的运输进行智能化追踪,对人和物进行智能识别和定位;在矿产行业中,为了保证施工人员的安全,需要对施工人员进行定位,以便于发生紧急情况下能顺利的展开救援;在无人驾驶中,更是将GNSS技术与视觉传感器进行结合,利用光学信息对汽车前方物体的动态进行识别和测量,这也是目前非常热门的一个研究方向。在未来多传感器的融合,尤其是以GNSS技术与视觉为核心的组合,将会成为更好的应用方案。
1GNSS技术在测量中的应用分析
由于本文篇幅有限,GNSS技术在测量方面的应用,本文主要讨论地面控制点和相机位姿单像空间后方交会解算的问题。

图1航空影像数据
以航空比例尺1:14000的航空影像数据为例,其相邻影像的重合度为85%,具体的解算流程如下:首先开始进行结算,并获得影像数据的比例尺、方位元素以及控制点的坐标,控制点的坐标以外业测量为准;然后将垂直拍摄的角度初始值设置为0,计算得出待定数的初始值;在将控制点的坐标转换成旋转矩阵,通过共线方程对控制点坐标的近似值进行计算,计算误差方程式、法方程式以及各项系数的表达式;最后对外方位元素进行迭代求解,并计算是否收敛。
 (1)
(1)
在解算外方位元素误差时可以使用公式(1)来进行计算。公式(1)中, 表示单位权的中误差,其计算公式如下:
表示单位权的中误差,其计算公式如下:
 (2)
(2)
在计算出地面控制点坐标和相机参数后,与外业实际测量数据进行比较,从图1中选取两张重叠像片,并通过上述计算过程对这两张像片的外方位元素进行计算,计算后的结果如表1所示:
表1后方交会解算的中误差
后方交会 | 像片1 | 像片2 |
中误差 | 中误差 | |
| 0.24561 | 0.16234 |
| 0.18121 | 0.10966 |
| 0.09324 | 0.04623 |
| 0.00032 | 0.00024 |
| 0.00021 | 0.00015 |
| 0.00011 | 0.00006 |
将两个像片中位差的计算结果与GNSS设备的测量结果进行对比。计算的结果如表2所示。
表2计算结果对比
外方位元素 | | | | | | |
像片1 | 0.091 | -0.025 | -0.043 | 0.018 | 0.003 | 0.001 |
像片2 | -0.219 | 0.291 | 0.694 | -0.028 | -0.005 | 0.007 |
通过对两个像片的后方交会进行计算,表明地面控制点和相机的位置较为准确和GNSS系统的测量结果相比,误差较小不会对最终结果产生影响。
2GNSS技术在视觉导航中的应用分析
视觉导航在进行里程计算的过程中需要提取特征点来作为匹配的基准,但是这种计算方式在进行实际使用时两种情况会导致错误的匹配:一是当地形中纹理特征相似或者出现重复时;二是地形中没有明显角点时。这两种情况的出现都无法通过特征点来进行定位和路线规划,实际的导航结果存在着不稳定性。视觉导航还存在另外一个比较严重的缺点就是在匹配和计算的过程中非常耗时,往往为了减少耗时,而尽可能的减少特征点的提取数量,但这样在匹配环节又降低了匹配成功的概率。因此为了解决视觉导航所存在的缺陷,并提高导航的准确率,因此将GNSS技术应用到视觉导航之中,可以在一定程度上提升移动载体的导航性能。
本文将GNSS技术与视觉导航系统进行结合,具体的措施有以下几点:一是由于GNSS定位采用WGS84坐标,而视觉导航系统的定位系统采用CML标系,在进行定位计算的过程中都需要将自身的坐标系统转换成WGS84坐标系统,但是这种转换也只是针对CML坐标系本身而言,与实际的WGS84坐标系统并没有直接联系,因此二者的结合首先就是要将坐标系统进行统一。在结合的过程中可以采用轨迹信息将视觉导航的定位结果纳入到GNSS坐标系统之中;二是由于视觉导航的轨迹信息相对粗糙存在着一定的误差,虽然视觉导航系统的误差来源于系统内部,这种误差的范围较小,但是在运行过程中会造成误差的积累,运行的时间越长这种误差的值就越大。因此就需要采用旋转矩阵对轨迹信息进行平滑处理以降低误差的影响。
 (3)
(3)
本文用 与
与 表示两个系统的坐标系,通过公式(3)进行二者之间的旋转。公式(3)中
表示两个系统的坐标系,通过公式(3)进行二者之间的旋转。公式(3)中 表示
表示 到
到 的旋转矩阵,
的旋转矩阵, 表示
表示 和
和 的平移向量。通过计算求解出坐标系中
的平移向量。通过计算求解出坐标系中 和
和 的最优解。当导航中的坐标点逐渐增多时,这两个数值也在不断发生变化。但在进行旋转时还应引入一个缩放因子,来进一步提高导航的定位精度,本文将这个系数设为
的最优解。当导航中的坐标点逐渐增多时,这两个数值也在不断发生变化。但在进行旋转时还应引入一个缩放因子,来进一步提高导航的定位精度,本文将这个系数设为 ,表达公式如下:
,表达公式如下:
 (4)
(4)
可以得出:
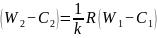 (5)
(5)
 (6)
(6)
因此,可以求出旋转矩阵最终的 和矩阵的平移向量
和矩阵的平移向量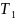 ,表达公式为:
,表达公式为:
 (7)
(7)
 (8)
(8)
最后根据实际情况将GNSS的数据与视觉导航输出的位置信息进行对齐,就可以在GNSS接收器中显示移动的轨迹从而实现最终的定位。
3结语
随着我国经济的发展,一种传感器所提供的定位和感知已经无法满足人们日常的实际需求,这对导航与测量技术提出了更高的要求,但由于这些技术本身存在着一定的局限性,并不利于这些技术未来的发展。本文将GNSS技术应用到视觉导航与测量之中以对其进行优化,从而解决这些技术存在的一些问题。
参考文献
[1]冯黎, 郭承军. 基于GNSS/SINS/双目视觉里程计的车载导航系统分析与设计[J]. 汽车技术, 2019(10).
[2]莫善会. GNSS与视觉里程计辅助IMU的行人导航方法研究[D]. 电子科技大学, 2019.
[3]王东, 范叶满, 薛金儒,等. 基于GNSS与视觉融合的山地果园无人机航迹控制[J]. 农业机械学报, 2019, 050(004):20-28.