两位数乘两位数笔算新算法初探

两位数乘两位数笔算新算法初探

廖永英

昆山国际学校   江苏省苏州市 215300

摘要：关于两位数乘两位数的笔算内容，学生计算比较容易出错，我国明朝的《算法统宗》里讲述了一种“铺地锦”的计算方法，根据这种方法的改编的一种新方法，不需要在计算乘法时进位，这样的计算方法简单易懂，不容易出错，是否可以尝试教学这种方法，本文把实践的过程及反思记录下来，让各位教育界的同仁们一起探讨。

苏教版小学数学第六册第一单元内容是《两位数乘两位数的笔算》，这个内容在学生刚学习时，发现很容易出错，主要存在两个方面的错误：

1、口算不够熟练，主要是进位加不熟悉、乘法口诀不熟练和加法与乘法的混淆。

错例1：“6×8＋4=54”,在计算48＋4时不仅速度慢，而且容易错；

错例2：“3×9=18”，这是乘法口诀不够熟练导致的，很多学生计算与“3”有关的乘法特别容易混淆，像3×7、3×8、3×9；

错例3：“3＋3=9”相加时容易算成乘法。

2 、计算步骤容易出错。有时一糊涂，会忘记谁和谁相乘。

错例：

错例中的496用的是62×8，计算方法没有掌握，算理没有理解。

虽然通过一定量的练习，学生正确率略有提高，但是也仍然容易出错。由于学生出错过多，于是思考：有没有更简单的方法呢？

“铺地锦”的方法以及新方法介绍

数学书上介绍了一种“铺地锦”的计算方法（苏教版三年级上册教材），在课堂上，学生明显对这种方法很感兴趣，不少学生表示很好理解，掌握起来很快，就是要画格子比较麻烦。有些学生还饶有兴趣地在课后做了些类似的题目给我看，看到学生对这种方法的喜爱。我想，能不能把这种方法变得更加简单呢？可不可以不画格子？怎样的形式比较方便实用？我在网上搜了一下，发现了一种类似的新方法：

这种方法其实就是“铺地锦”的另一种表达方式，先竖着两个数相乘（十位乘十位，个位乘个位），分别写在千位、百位和十位、个位；然后交叉相乘（第一个乘数十位乘第二个乘数个位；第一个乘数个位乘第二个乘数十位），得数写在百位和十位。最后把三个数相加。

这种方法的优势：中间的几步只有乘法，没有进位，直接把乘得的积写在下面；最后一步只有加法。这样学生不容易混淆。

接下来有一个班级我教学了这种方法，学生们学得很快，感觉比较简单，在课上学生们表示这种方法更愿意使用。

这种方法也需要一定的练习才能熟练掌握，学生们在练习的过程中，慢慢地更熟练地掌握了。

新方法算理

但是这种方法的算理呢？计算都要和算理结合在一起，才更有意义，才能更深刻地理解它。

以13×12为例：

13×12可以表示12个13相加（图中有12行，每行13个）。那么，我们把13×12分成4个模块：

10×10、3×2、10×3、10×2（分别是上面A\B\C\D）

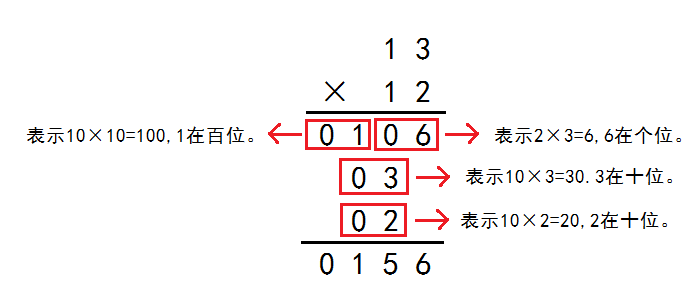
每次相乘都尽量让学生占两个数位，这样不容易出错，而且每道题的格式都一模一样，容易记忆。

这种方法被发现后，我和同事们都觉得这种方法很好，学生掌握会更快。但事实如何，我们用实际情况说话。

我教学了两个班级，甲班级两种方法都教了，但新方法是常用方法教学后一周后才学的，乙班级只教书本上的常用的方法。

刚开始，甲班级的正确率没有乙班级高。我在思考为什么？照理说这种方法简单，应该正确率更高，找了几个学生谈话，总结反思了一下，主要有三个原因：

（1）学生们觉得两种方法都学，有些混淆；

（2）让学生自主选择计算方法，小部分学生先入为主，熟悉了书本上教学的方法。

（3）在刚开始教学时，教学的方法是：最高位是“0”时可以省略不写，导致学生该写“0”的时候反而没写。

主要错误如下：

（1）有十几位学生的错误都是个位相乘得8，应该写“08”，而不是8，这里的错误最多。

(2)有个别学生是粗心导致的错误，例如最后加法错误;相乘时数字乘错;

乘法口诀出错。

针对学生的这些错误，改变策略，首先让甲班级学生只接触新方法，使新方法更加熟练；乙班级学生还是使用常用的方法；其次，书写格式规范化，规定把“0”补齐，相乘得一位数时，用“0”占位。经过一周的练习，甲班级正确率明显更高，而且学生们熟练了这种方法，计算速度很快。

接下来给学生的测试，每个班级25道计算题，分别统计了正确率：

甲班：总人数45人，全对37人，错3题以上人数0人。

乙班：总人数45人，全对28人，错3题以上人数2人。

在两个班级学生情况相似的情况下，甲班的成绩略高，学生计算速度更快。此时感觉新方法的教学还是成功的，值得推荐的。

反思探讨

接下来值得思考的是：这种方法能否推广？这种方法对三位数乘两位数的竖式学习有影响吗？

于是我继续研究了三位数乘两位数笔算的新方法，发现还是有很多问题：

这样的竖式明显太麻烦，使用不方便。如果简写，又达不到简便的效果，也就是说三位数乘两位数使用这样的方法是不可取的。那么在四年级学习这部分内容时如何处理？如果新方法使用熟练了，四年级又需要重新熟悉课本上使用的常规方法，这样反而学生容易混淆，导致错误。

这一次的两位数乘两位数的笔算新方法的实践研究，开始发现时感觉很兴奋，觉得自己找到了更好的方法。但是后来慢慢发现问题：没有考虑到之后的延伸学习，对后续三位数乘两位数的笔算学习存在较大的阻碍。我把这次的实践探索称为“一时的冲动” ！不过，我也认为，实际生活中，两位数乘两位数的计算还是非常常用的，多学习一种方法，一是可以用来检验另一种方法算得对不对，二是可以加快计算的速度，降低计算的难度。对于理解能力较好的学生来说，应该算是多学习了一种技能。