基于多项式拟合的最优利率的确定-中国期刊网

基于多项式拟合的最优利率的确定

张雅洁 1 韩亚楠 2 吕泽华 3

1 华北理工大学数学建模创新实验室河北唐山 063210 2 华北理工大学数学建模创新实验室河北唐山 063210 3 华北理工大学管理学院河北唐山 063210

前言：中小微企业是国家国民经济和社会发展的重要基础，是刺激国家经济稳步发展的强大动力，在扩大就业率、改进人民生活质量、促进社会稳定、国家税收、市场经济发展等方面起到了举足轻重的作用。而近年来由于中小微企业具有贷款不良率高，信用差的特点，出现了银行基层人员“惜贷”“拒贷”的现象，为此国家逐步建立了“敢贷、愿贷、能贷、会贷”的机制，来调动银行基层人员的积极性，主推小微企业加速信贷投放。

实际中，由于中小微企业规模相对较小，也缺少抵押资产，因此银行通常是依据信贷政策、企业的交易票据信息和上下游企业的影响力，向实力强、供求关系稳定的企业提供贷款，并可以对信誉高、信贷风险小的企业给予利率优惠。银行首先考虑中小微企业的实力、信誉以选取销售金额、采购金额、销售采购比、销售订单数、采购订单数、信誉等级以及违约情况作为指标对其信贷风险做出评估，然后依据信贷风险等因素来确定是否放贷及贷款额度、利率和期限等信贷策略。为了在保证中小微企业获得较多贷款的同时银行获得较高的利润，就需要确定一个对于企业和银行来说均最优的最优利率。

摘要：选取销售金额、采购金额、销售采购比、销售订单数、采购订单数、信誉等级以及违约情况作为评价公司风险系数的评价指标体系。对与其相关的数据进行分析处理，运用熵权法和成对比较矩阵以及TOPSIS模型最终将指标的相关数据转化为公司对应的分数，以此分数的高低来评价公司的风险系数。考虑客户流失率与年利率有关，利用多项式拟合得到不同信誉等级客户流失率随信誉等级变化的函数关系；最后综合考虑贷款金额、客户流失率等对最优利率的影响，利用利息公式构建银行盈利模型，运用最优化方法进行求解，用spss对贷款中总额、风险等级、最优利率等数据进行拟合，最终得到不同风险等级下最优利率与贷款总额关系的函数。

关键词：熵权法、TOPSIS、多项式拟合、最优利率

一、基于多项式拟合的最优利率模型

（一）风险系数的量化：

以销售金额、采购金额、销售采购比、销售订单数、采购订单数、信誉等级和违约情况作为该公司的信贷风险评价指标体系。对该定性指标结合所查到123家公司的相关数据进行分析处理将其转换为定量指标。对定量指标利用熵权法和成对比较矩阵得到两个主客观权重，对其进行加成得到综合权重，最后利用TOPSIS模型进行打分，以最终得到的分数来量化公司的风险系数。

（二）模型的建立：

将公司风险系数对应的得分映射到其自身对应的信誉等级指标上，发现不同信誉等级对应的打分分布在不同区间，因此，通过对不同信誉等级的筛选得出其分别对应的风险系数的打分平均值，得到风险系数分布与信誉等级的关系如下所示：

表 1各信誉等级的风险系数分布

信誉等级	A	B	C
风险系数	0-11.32%	11.32%-16.71%	25.4%-49.1%

由于银行给出的利率不同时，所对应的客户流失率也不同，即使信誉等级较高的银行的客户也会倾向于选择利率较低银行进行贷款，从而造成该信誉等级较高的银行的客户流失，因此要选择较恰当的利率使客户流失率保持在合理范围内，从而保证银行利益最大化的同时保证更多公司可以贷到相应的贷款金额。

结合已知123家公司的客户流失率与银行信誉等级、所给利率的相关数据进行多项式拟合可得到不同信誉等级下客户流失率随贷款年利率变化而变化的函数关系的拟合图如下所示：

图- 1流失率随利率变化图

上图是根据123家公司的数据得到的银行关于不同信誉等级时利率的选取对客户流失率的影响曲线图。可以观察到，对于信誉等级A的企业客户，其流失率曲线整体是高于信誉等级B、C的客户的，可见信誉等级A的客户选择银行贷款时，其选择意愿更容易受到银行所给的利率影响，而信誉等级B、C的客户其客户流失率曲线的变化重合率较高，尽管其客户流失率也受到贷款年利率的影响，但是对于利率较低的选择倾向并没有信誉等级A的客户高。而银行选择信贷对象时，会更倾向于选择信誉评级高，实力较强的企业（但是如果利率的选择失败其流失率也会更高）。因此需要综合各个企业的实际情况、风险评估以及其违约率合理的给出对于不同信誉等级企业的利率，使得银行获得的收益期望达到最高。

对以上三个等级的客户流失率变化曲线进行多项式拟合，经过检验我们发现选择四次多项式拟合的效果相对理想，从而得到不同信誉等级客户流失率随信誉等级变化的函数关系表达式如下所示：

由利息公式可知，利息＝本金×利率×时间，对于银行而言其通过对企业进行放贷获得利益，即企业所需向银行支付的利息，综合考虑流失率，信誉等级，以一年为期得到银行盈利表达式如下所示：

其中，表示以一年为期得到银行的盈利，表示固定借贷额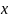，表示4%-15%的年利率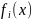，中的表示不同信誉等级。为使银行尽可能多的获得盈利，利用最优化模型调整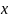的值使达到最大。得到不同贷款额度下的风险系数和最优利率如下表所示：

表 2不同贷款额度下的风险系数和最优利率

贷款金额	风险系数	最优利率
1亿	0-11.32%	5.13%
	11.32%-16.71%	5.4%
	25.4%-49.1%	5.94%
5000万	0-11.32%	4.845%
	11.32%-16.71%	5.1%
	25.4%-49.1%	5.61%
1000万	0-11.32%	4.489%
	11.32%-16.71%	4.725%
	25.4%-49.1%	5.198%
500万	0-11.32%	5.045%
	11.32%-16.71%	5.31%
	25.4%-49.1%	5.845%
100万	0-11.32%	5.368%
	11.32%-16.71%	5.65%
	25.4%-49.1%	6.125%

由上一步计算的不同贷款额度下的风险系数和最优利率表得到：

表 3 风险等级最优利率

贷款总额	风险等级最优利率
	0-11.32%	11.32%-16.71%	25.4%-49.1%
1亿	5.13%	5.4%	5.94%
5000万	4.845%	5.1%	5.61%
1000万	4.489%	4.725%	5.198%
500万	5.045%	5.31%	5.845
100万	5.368%	5.65%	6.125%