潘瑞平
摘要: 函数零点是高考考查的一个热点问题,尤其是与零点有关的参数取值范围问题,是近年来高考考查的热点问题.零点问题渗透了数学思想与数学能力的考查,较好地反映了学生分析和解决问题的能力.本文对一道经典的含参的零点试题进行分析,寻求已知函数零点个数求参数问题的解题策略.
关键词: 零点 含参 函数 方程 分离变量
新课标下的高考越来越注重对学生的综合素质的考察,函数的零点问题便是一个考察学生综合素质的很好途径,它主要涉及到基本初等函数的图象,渗透着转化、化归、数形结合、函数与方程等思想方法,在培养思维的灵活性、创造性等方面起到了积极的作用。
关于函数的零点问题高中所涉及的主要知识点归纳如下:
根据函数零点的定义:对于函数 ,把使
,把使 成立的实数
成立的实数 叫做函数
叫做函数 的零点。
的零点。
方程 有实数根
有实数根 函数
函数 的图象与
的图象与 轴有交点的横坐标
轴有交点的横坐标 函数
函数 有零点。围绕三者之间的关系,在高考数学中函数的零点的个数问题转化成利用导数结合图像的变动将两个函数的图像的交点问题。
有零点。围绕三者之间的关系,在高考数学中函数的零点的个数问题转化成利用导数结合图像的变动将两个函数的图像的交点问题。
零点的存在性定理:如果函数 在区间
在区间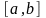 上的图象是连续不断的一条曲线,并且有
上的图象是连续不断的一条曲线,并且有 ,那么函数
,那么函数 在区间
在区间 内有零点。既存在
内有零点。既存在 ,使得
,使得 ,这个
,这个 也就是方程的根。
也就是方程的根。
近几年的数学高考中频频出现零点问题,其形式逐渐多样化,其中常见的一种已知函数的零点的个数求参数的取值范围问题,本文以一道经典例题探讨处理此类问题的常用方法.
例题:已知 有唯一零点,求实数
有唯一零点,求实数 取值的集合.
取值的集合.
法一:(完全分离变量)
分析:根据函数 有零点
有零点 方程
方程 有实数根
有实数根 函数
函数 的图象与
的图象与 轴有交点的横坐标,围绕三者之间的关系,我们可以函数的零点问题转化为两个函数交点问题.常常通过分离变量的方法来求参数的范围.
轴有交点的横坐标,围绕三者之间的关系,我们可以函数的零点问题转化为两个函数交点问题.常常通过分离变量的方法来求参数的范围.
讨论如下:
 有唯一正零点
有唯一正零点 有唯一正根。
有唯一正根。
当 ,可知
,可知 使得
使得 此时
此时 无正零点。(舍)
无正零点。(舍)
当 ,即
,即 ,
, ,
,
设


 在
在 减,
减, 增,所以
增,所以


点评:已知函数零点的个数,求参数范围常用分离变量,但此方法缺点在于新构建的函数g(x)在原来的定义域范围内不连续,若学生往往考虑不到这一点,容易丢了 的范围。如何避免出现以上情况,我们可以对构造函数稍作修改。如下方法:
的范围。如何避免出现以上情况,我们可以对构造函数稍作修改。如下方法:
法二:(完全分离变量)
当m=0, 无正零点.(舍)
无正零点.(舍)
当 ,设
,设 ,
,
 在
在 增,
增, 减,
减, ,
, 所以
所以
点评:方法二也是完全分离变量,但较方法一构造的函数 在
在 上连续,避免了分母没有意义的情况,更利于学生正确求出参数
上连续,避免了分母没有意义的情况,更利于学生正确求出参数 的取值范围.
的取值范围.
当然,分离变量也可以是不彻底的,即有时候进行部分分离变量求参数范围更简洁。
法三:(不完全分离变量)
 有唯一正零点
有唯一正零点 有唯一正根。
有唯一正根。






点评:局部分离变量构成两个较为熟悉且简单函数,处理起来较彻底分离相对简单一些。
也可以如下进行部分分离变量:
法四: (解法同法三)
(解法同法三)
点评:法四局部分离变量比法三更好,因为法四中左右两边函数学生比较熟悉。
法五:(直接讨论)


点评:一般来说若不好分离变量,则可以采用第五种方法,而近几年高考压轴题往往用法五。
上述例子运用了五种方法求解,法一至法四本质上基本相同,都是把f(x)=0转化为g(x)=h(x),把函数的零点问题转化为函数y=g(x)与y=h(x)的交点问题,只需考虑如何分离会构造出比较简单而熟悉的函数进行研究。若不好分离则采用方法五对参数进行分类讨论来研究f(x)与x轴交点的情况。值得一提的是,各种类型各种方法并不是完全孤立的,虽然方法表现的不同,但其实质却都与求函数的零点是等价的,这也正体现了数学中的“统一美”。
总之,此类问题考察学生思维的灵活性,创造性,而我们应该在平时有意识地训练自己选择何种方法处理含参数的零点问题更简单。
参考文献:
[1]梁小金;;运用导数解决含参函数问题的策略[J];中学教学参考;2010年05期
[2]张柳;;关于用导数研究零点问题的一点思考[J];考试周刊;2020年60期

4