不同GNSS 解算策略对平差与高程拟合精度的影响研究

不同 GNSS 解算策略对平差与高程拟合精度的影响研究

梁相国

柳州勘察测绘研究院有限公司

摘要: 以现代测绘基准建设的短基线 GNSS 网作为应用实例，研究比较采用对流层延迟估计与对流层延迟不估计两种短基线解算策略在 GLOBK 软件中的平差精度，并结合已有二等水准正常高，生成两套 GNSS/水准点的成果，通过似大地水准面计算软件，利用地球重力场模型对两种策略下的平差结果进行模型拟合验证，以此评价其平差精度与拟合精度的影响。结果显示，采用对流层延迟不估计的基线解算策略的 GLOBK 平差精度更高，且其拟合效果更好。

关键词: 对流层延迟；GLOBK；平差精度；GNSS/水准拟合

0 引言

GNSS 数据处理是一个复杂的过程，其受到测站的环境、天气状况、测站观测质量、测站距离与高差、观测时长、卫星质量、电离层与对流层模型改正等因素的影响。本文以某地区应用区域的短基线 GNSS－C级网为例，使用 GAMIT 软件，采用对流层延迟估计与不估计的两种基线解算策略，即在 sestbl．中前者将 Zenith Delay Esti-mation 设置为 Y，后者将 Zenith Delay Estimation 设置为 N，然后使用 GLOBK 软件分别进行平差计算处理，验证与比较这两种不同短基线的解算策略在 GNSS 网平差计算中精度的影响，并利用似大地水准面计算软件进行曲面拟合，以进一步分析其平差精度对 GNSS/水准拟合所带来的影响。

1 原理与方法

1．1 GLOBK 平差计算

利用 GLOBK 实现 GNSS 综合解，分为 3 步: 1) 将所有的准观测值文件转换为 GLOBK 能识别的格式; 2) 合并所有准观测文件中的松弛约束估计信息到一个解中; 3) 通过对选定的部分测站的坐标和速度施加一定的约束，为最终解确定一个统一的参考框架。GLOBK 采用的是卡尔曼滤波法，设 k 时段 GNSS 数据的观测方程式为:

y_k= A_kx_k+ v_k( 1)

式中，k 为观测时段号; yk为观测值与理论计算值的差值向量，理论计算值由参数的先验值计算而来; Ak为误差方程式的系数矩阵; xk为待估参数向量，是相对于参数先验值的改正值向量; vk为观测值噪声的残差向量; 这里设第 k 时段的参考历元为 tk。 方程( 1) 还满足:

E( v_k) = 0; E( v_kv^T_k) = V_k; E( v_kv^T_j) = 0 k ≠ j ( 2)

参数 x_k的状态转移方程为:

x_{k + 1}= S_kx_k+ w_k ( 3)

式中，k + 1 表示 GPS 观测的第 k + 1 时段，相应的参考历元记为 t_{k + 1}; S_k表示 t_k时刻的状态转移矩阵; w_k为 t_k到 t_{k + 1}时刻之间影响状态转移的随机扰动向量( 对于非随机参数 w_k= 0) ; W_k为协方差阵，且满足: E( w_k) = 0;E( v_kw_k) = 0; E( w_kw_j) = 0( 当 k ≠ j 时) ; E( w_kw_j) =w_k( 当 k = j 时)。

从 t_k到 t_{k + 1}时刻的预报公式为:

x^k_{k + 1}= S_kx^k_k ( 4)

C^k_{k + 1}= S_kC^k_kS^T_k+ W_k ( 5)

从 t_k到 t_{k + 1}时刻的修正公式为:

( 6)

( 7)

式中，K 为卡尔曼增益矩阵;

K = C^k_{k + 1}A^T_{k + 1}( V_{k + 1}+ A_{k + 1}C^k_{k + 1}A^T_{k + 1})^－1 ( 8)

以上各式中的上标 T 表示向量或矩阵的转置。 、 表示 t_{k + 1}时刻参数的最佳估计值和协方差矩阵。

限于篇幅，详细的 GLOBK 数据处理原理。

针对应用实例区域控制网的 GLOBK 处理步骤流程如图 1 所示，详细的命令操作过程。

图 1 GLOBK 数据处理流程

1．2 GNSS 高程拟合计算

本文基于地球重力场模型及 GNSS/水准数据，采用二次曲面拟合法构建应用区域似大地水准面模型，并对其进行精度分析。曲面拟合法是认为高程拟合在一定范围内变化平缓的前提下，将高程异常近似地看作是一定范围内各点坐标的曲面函数。设测站点的高程异常与其平面坐标的函数关系为

ξi= f( x_i，y_i) + v_i ( 9)

式中，f( x_i，y_i) 为所选定的曲面函数，也即 ξ_i的趋势值; v_i为其残差。当选择多项式曲面拟合时，则有f( x_i，y_i) = b₀+ b₁x_i+ b₂y_i+ b₃x²_i+ b₄y²_i+ b₅x_iy_i ( 10)

式中，b₁( i = 0，1，2，…，5) 为待定系数; ( x_i，y_i) 为 i点的平面坐标

( 11)

式中，( x，y)为中心( 归算中心的坐标) 。

根据上述方法，采用似大地水准面计算软件，结合地球重力场模型，对采用对流层延迟估计与对流层延迟不估计策略下的两种平差结果进行模型拟合验证，以此评价其平差精度与拟合精度的影响。

2 应用实例与结果分析

某地区现代测绘基准建设的GNSS－C 级网为例，该网属低纬度亚中亚热带季风气候，常年高温湿润多雨，大气环流主要是季风环流，地貌属于典型的喀斯特地貌，测站点位间距平均为 11 km，距离较短。控制网共有 44 个同步环，外业观测按规范GNSS － C 级的测量要求进行，并在此基础上将观测时长增加至 20 h 以上，以获得较长时段的数据观测量。观测时间为 9—10 月，天气状况稳定，多为晴天或多云，减少了受台风、雨季、气温骤变等引起的对流层延迟误差因素的影响。通过使用 GAMIT10．6 进行基线解算，分别采用对流层延迟估计与对流层延迟不估计两种策略进行基线解算，再使用 GLOBK 分别进行网平差计算，以进一步研究基线解算策略与平差精度的关系。为了获得高精度的起算基准，引入了应用区域 GNSS－B 级网基线解算结果，并以此作为该点坐标值作为平差计算的起算基准。此次 GNSS 网的三维约束平差结果建立了该地区在CGCS2000 框架下的三 维 大地 坐 标基准，其 中 CGCS2000框架下的三维大地坐标基准与 ITＲF97 框架( 2000．0 历元) 的基准一致。利用基线解算结果 H－file 进行 GLOBK 平差计算。通过平差处理，以对流层延迟估计与不估计的平差结果globk．org文件进行汇总验证分析，结果比对如图 2 至图 4所示。

图 2 GLOBK 平差 N 方向精度

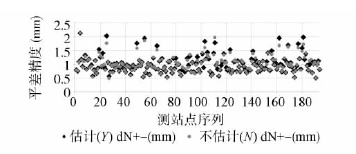
图 3 GLOBK 平差 E 方向精度

图 4 GLOBK 平差 H 方向精度

从图 2 至图 4 可得，在 GLOBK 平差中，采用对流层延迟估计与不估计的解算策略，在 N、E 方向上的平差精度接近，而对流层延迟不估计 H 方向上的平差精度优于对流层延迟估计，且精度提高了 1 倍以上。平差精度统计见表 1。

表 1 GLOBK 平差精度统计

为了进一步验证 GLOBK 平差精度对于似大地水准面计算的精度影响，利用该区域布设的共 142 个高程异常控制点( 如图 5 所示) ，分别求取对流层延迟估计的GLOBK 平差后大地高与对流层延迟不估计的 GLOBK 平差后大地高，生成两套 GNSS/水准点的成果，在不添加重力数据情况下，利用地球重力场模型，分别与 GNSS/水准点成果进行初步似大地水准面拟合计算，分析利用模型求取的正常高与二等水准正常高的差值，以此评价其平差精度与拟合精度的影响。拟合精度比较如图 6 所示。

由图 5、图 6 可得，利用重力场模型计算得到的 142个高程异常控制点拟合内符合情况，其中经对流层延迟估计后平差结果的拟合精度为± 1．275 7 cm，平均值为－0．044 7 cm，最大值为 4．203 0 cm，最小值为－3．687 0 cm;经对流层延迟不估计后平差结果的拟合精 度 为±0．892 1 cm，平均值为－0．012 8 cm，最大值为 3．85 2 cm，最小值为－2．90 6 cm。经比较分析，应用实例 GNSS 网中采用对流层延迟不估计的 GLOBK 平差精度值无论从整体的拟合精度、最大值、最小值及平均值来看，均比采用对流层延迟估计的值要小，但从数据上看，最大值与最小值跳动较大，与均值偏离较多，且均存在个别大于 3 倍中误差的粗差点情况。

图 5 高程异常控制点分布

图 6 GNSS/水准拟合精度

3 结束语

1) 对于短基线 GNSS 网，采用对流层延迟不估计的基线解算策略，其平差精度比采用对流层延迟估计解算策略更高。因此，若在测站间距离较短，且气候状况稳定的情况下，宜优先选择前者，以获得精度更高的大地高。

2) 一 方面结合已有二等水准正常高，生成两套GNSS / 水准点成果，引入地球重力场模型进行的曲面拟合比较，其 GLOBK 平差精度越高，GNSS/水准拟合效果越好; 另一方面，采用对流层延迟不估计的 GLOBK 平差结果的拟合精度达到±0．892 1 cm，能基本满足似大地水准面拟合的精度，但从数据上看，最大值与最小值跳动较大，与均值偏离较多，且有个别大于 3 倍中误差的粗差点，证明在缺少重力数据的情况下会带来一定的影响。因此，为实现现代测绘基准建设应用的高精度区域似大地水准面，除了选择更优的 GNSS 基线解算策略与平差方法，高精度的高程基准数据及高精度重力数据的采集利用同样重要。

参考文献:

［1］ 安向东，杨登科．测站间高差对短时段 GPS 基线解算的影响［J］． 大 地 测 量 与 地 球 动 力 学，2016，36 ( 6) :534－538．

［2］ 舒海翅，郑敏．河谷区对流层延迟对 GPS 短基线解算的影响分析［J］．人民长江，2010，41( 20) : 60－62．

［3］ 章迪，郭际明，陈雪丰，等．对流层延迟估计对高差较大短基线解算的影响［J］．大地测量与地球动力学，2014，

34( 2) : 146－149．

［4］ 王巍．对流层延迟对高差较大 GPS 测站短基线时间序列的影响分析［J］．大地测量与地球动力学，2018，38

( 5) : 504－509．

［5］ 朱璇，苗岳旺，于亮．QOCA 和 GLOBK 软件处理高精度GNSS 网结果对比分析［J］． 大地测 量 与地 球 动 力 学，

2017，37( 11) : 1 206－1 210．

［6］ 王健，刘宗强，朱亚兵．不同解算策略下的 GNSS 区域网平差分析［J］．导航定位学报，2018，6( 1) : 97－102．

［7］ 邱荣海，成英燕，席伟．利用 GLOBK 软件提高平差精度的策略［J］．导航定位学报，2015，3( 4) : 100－103．

［8］ 王艺希，秘金钟，徐彦田，等．卡尔曼滤波方法的 BDS/GLONASSＲTK 定位算法［J］． 测绘科学，2017，42( 12) :112－117．

［9］ 张潘，余代俊，张玉刚，等．GPS 高程拟合方法研究及精度对比试验［J］．测绘通报，2015( 9) : 54－56．

［10］ 谭衍涛，黄健鹏，黄国荣，等．重力场模型及 GNSS/水准的区域似大地水准面精化［J］．测绘科学，2016，41( 4) :5－9．